人教版数学七年级下册 8.3 实际问题与二元一次方程组 课件1(共21张PPT)
文档属性
| 名称 | 人教版数学七年级下册 8.3 实际问题与二元一次方程组 课件1(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 10:35:40 | ||
图片预览








文档简介
(共21张PPT)
实际问题与二元一次方程组
学习目标
1.用二元一次方程组解决实际问题.
2.体会数学建模的思想.
重点:理解题意,寻求题中等量关系列方程.
难点:寻找“关键词”,列出等量关系.
昨天,我们一家8个人去红山公园玩,买门票花了34元。
哦,那你们家去了几个大人?几个小孩呢?
真笨,自已不会算吗?成人票5元每人,小孩3元每人啊!
聪明的同学们,你能帮他算算吗?
轻松练习
《孙子算经》
《孙子算经》是中国古代最重要的数学著作,
约成书于四、五世纪.现在的传本共三卷,
卷上叙述算筹记数的纵横相间制度和筹算乘除法;
卷中举例说明筹算分数算法和筹算开平方法;
卷下记录算题,不但提供了答案,而且还给出了解法.
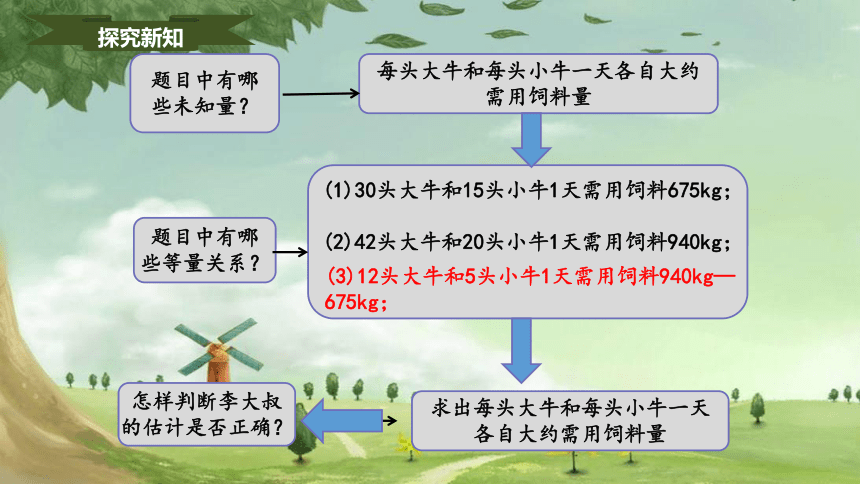
怎样判断李大叔的估计是否正确?
求出每头大牛和每头小牛一天各自大约需用饲料量
(1)30头大牛和15头小牛1天需用饲料675kg;
(2)42头大牛和20头小牛1天需用饲料940kg;
每头大牛和每头小牛一天各自大约需用饲料量
题目中有哪些未知量?
题目中有哪些等量关系?
(3)12头大牛和5头小牛1天需用饲料940kg—675kg;
探究新知
《算法统宗》原名《直指算法统宗》,是明清间影响较大的一部以珠算盘为计算工具的数学著作。万历二十年(1592)程大位著,并由作者在屯溪的宾渠旅舍刊行。
本书17卷,595个应用题,大都摘自传本数学书籍,而以珠算术求解。卷1、2为数学术语之解释,大数、小数之进法,度量衡单位,珠算口诀及其在珠算盘中的用法举例。卷3—12为应用问题解法汇编。各卷依次仍以《九章算术》章名为标题,只是将粟米改为粟布。卷3方田章记载了他创制的测量田地的竹制“丈量步车”,类似于今之皮尺。卷6、7中记载了开平方、开立方的珠算术。大约同时成书的朱载堉的《算学新说》亦载此法,可知已为当时流行的方法。卷13—16为难题汇编,采用诗词形式意义隐晦,其难在此。卷17为杂法,为不能归于前几卷的各种算法。本书的珠算术以定位、留头乘法、归除为重点,编写上注重基本算法,精讲多练,因而易学易懂。
《算法统宗》
长18米的钢材,要锯成10段,而每段的长只能取“1米或2米”两种型号之一,小明估计2米的有3段,你们认为他估计的是否准确?为什么呢?那2米和1米的各应取多少段?
探究新知
1. 某电台在黄金时段的2分钟广告时间内,
计划插播长度为15 秒和30秒的两钟广告。
15 秒广告每播1 次收费0.6 万元,30 秒广
告每播 1 次收费1 万元,若要求每种广告
播放不少于2 次,问:
⑴ 两种广告的播放次数有几种安排方式?
⑵ 电视台选择哪种方式播放收益最大?
知识创新
《算法统宗》井深及绳长问题
原文:绳测进井深。 假若井不知深,先将绳三折入井,绳长四尺;后将绳四折入井,亦长一尺。问井深及绳长各若干
大意是说:用绳子测量井深,如果将绳子三折测井,井口外留绳子四尺;如果将绳子四折测井,那么
井口外余下一尺。问井深几尺 绳长几尺
A地
B地
长青化工厂
公路80km
铁路150km
原料
产品
1.5元/(吨·千米)
1.2元/(吨·千米)
公路运费:15000元 铁路运费:97200元
长青化工厂用汽车从A地购买一批原料运回工厂,制成产品后用火车运到B地。工厂与A地相距80千米,与B地相距150千米。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输支出公路运费15000元,铁路运费97200元。求工厂从A地购得的原料有多少吨?制成的产品有多少吨?
合作探究
检鼠妈妈采松子,晴天每天可以采20个,雨天每天只能采12个,它一连共采了112个,平均每天采14个,问这几天当中有几天晴几天下雨?
据以往的统计资料,甲、乙两种作物的单位面积产量的比是1:1.5,现要在一块长200m,宽100m的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量的比是3:4(结果取整数)?
分析:如图所示,一种种植方案为:甲、乙两种作物的种植区域分别为长方形AEFD
和BCFE。设AE=xm,BE=ym,根据问题中涉及长度、产量的数量关系,列方程组
,
。
解这个方程组,得
x= ,
y= ,
过长方形土地的长边离一端约 处,把这块地分为两个长方形。较大一块地种 种作物,较小一块地种 种作物。
x
y
A
B
C
D
E
F
x+y=200
100x:1.5×100y=3:4
106m
甲种
乙种
1.《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何 ”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行.问人与车各多少 设有x人,y辆车,可列方程组为
中考链接
问题1 公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km)是什
么意思?
如:把2吨货物从A地运到100千米外的B地,
经公路运输需要支付:
公路运价:经公路运输1吨货物行驶1千米需1.5元
铁路运价:经铁路运输1吨货物行驶1千米需1.2元
1.5×2×100=300元,
1.2×2×100=240元
运输费 = 运价 × 质量 × 路程
经铁路运输需要支付:
合作探究
练一练:
1、两种枕木共300根,甲种枕木的总重量比乙种枕木的总重量轻1吨,如果每根枕木甲种重46千克,乙种重28千克,两种枕木各多少根?
2、蔬菜批发站有一批青菜分给两个学校的食堂,甲校食堂分得的5倍比乙校食堂分得的6倍少10kg;甲校食堂分得的3倍与乙校食堂分得的2倍的和是470kg。甲、乙两校食堂各分得青菜多少?
《九章算术》是中国传统数学的重要著作,方程术是它的最高成就.其中记载:今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?译文:今有人合伙购物,每人出8钱,会多3钱:每人出7钱,又会差4钱,问人数、物价各是多少?
中考链接
设产品为x吨,原料为y吨。
1.2·y ·120
1.5·y·10
1.5·x ·20
1.2·x ·110
运输费 = 运价 × 质量 × 路程
有大小两种货车,2辆大车与3辆小车
一次可以运货15.50吨,5辆大车与6辆小
车一次可以运货35吨。
求:3辆大车与5辆小车一次可以运货
多少吨
分析:要解决这个问题的关键是求每辆
大车和每辆小车一次可运货多少吨
解决此题的
关键是什么?
问题三
一艘轮船顺流航行45千米需要3小时,逆流航行65千米需要5小时,求船在静水中的速度和水流速度。
解:设船在静水中的速度为x千米/时,水流的速度为y千米/时,根据题意,得
答:船在静水中的速度及水流的速度分别为14千米/时、1千米/时.
解这个方程组得,
即
合作探究
例1:据以往的统计资料,甲、乙两种作物的单位面积产量的比
是 1:1.5,现要在一块长200m,宽100m的长方形土地上种
植这两种作物,怎样把这块地分为两个长方形,使甲、乙
两种作物的总产量的比是 3 : 4 (结果取整数)
A
B
C
D
甲种作物的总产量 = 甲的单位面积产量×甲的种植面积
乙种作物的总产量 = 乙的单位面积产量 ×乙的种植面积
同学们再见
实际问题与二元一次方程组
学习目标
1.用二元一次方程组解决实际问题.
2.体会数学建模的思想.
重点:理解题意,寻求题中等量关系列方程.
难点:寻找“关键词”,列出等量关系.
昨天,我们一家8个人去红山公园玩,买门票花了34元。
哦,那你们家去了几个大人?几个小孩呢?
真笨,自已不会算吗?成人票5元每人,小孩3元每人啊!
聪明的同学们,你能帮他算算吗?
轻松练习
《孙子算经》
《孙子算经》是中国古代最重要的数学著作,
约成书于四、五世纪.现在的传本共三卷,
卷上叙述算筹记数的纵横相间制度和筹算乘除法;
卷中举例说明筹算分数算法和筹算开平方法;
卷下记录算题,不但提供了答案,而且还给出了解法.
怎样判断李大叔的估计是否正确?
求出每头大牛和每头小牛一天各自大约需用饲料量
(1)30头大牛和15头小牛1天需用饲料675kg;
(2)42头大牛和20头小牛1天需用饲料940kg;
每头大牛和每头小牛一天各自大约需用饲料量
题目中有哪些未知量?
题目中有哪些等量关系?
(3)12头大牛和5头小牛1天需用饲料940kg—675kg;
探究新知
《算法统宗》原名《直指算法统宗》,是明清间影响较大的一部以珠算盘为计算工具的数学著作。万历二十年(1592)程大位著,并由作者在屯溪的宾渠旅舍刊行。
本书17卷,595个应用题,大都摘自传本数学书籍,而以珠算术求解。卷1、2为数学术语之解释,大数、小数之进法,度量衡单位,珠算口诀及其在珠算盘中的用法举例。卷3—12为应用问题解法汇编。各卷依次仍以《九章算术》章名为标题,只是将粟米改为粟布。卷3方田章记载了他创制的测量田地的竹制“丈量步车”,类似于今之皮尺。卷6、7中记载了开平方、开立方的珠算术。大约同时成书的朱载堉的《算学新说》亦载此法,可知已为当时流行的方法。卷13—16为难题汇编,采用诗词形式意义隐晦,其难在此。卷17为杂法,为不能归于前几卷的各种算法。本书的珠算术以定位、留头乘法、归除为重点,编写上注重基本算法,精讲多练,因而易学易懂。
《算法统宗》
长18米的钢材,要锯成10段,而每段的长只能取“1米或2米”两种型号之一,小明估计2米的有3段,你们认为他估计的是否准确?为什么呢?那2米和1米的各应取多少段?
探究新知
1. 某电台在黄金时段的2分钟广告时间内,
计划插播长度为15 秒和30秒的两钟广告。
15 秒广告每播1 次收费0.6 万元,30 秒广
告每播 1 次收费1 万元,若要求每种广告
播放不少于2 次,问:
⑴ 两种广告的播放次数有几种安排方式?
⑵ 电视台选择哪种方式播放收益最大?
知识创新
《算法统宗》井深及绳长问题
原文:绳测进井深。 假若井不知深,先将绳三折入井,绳长四尺;后将绳四折入井,亦长一尺。问井深及绳长各若干
大意是说:用绳子测量井深,如果将绳子三折测井,井口外留绳子四尺;如果将绳子四折测井,那么
井口外余下一尺。问井深几尺 绳长几尺
A地
B地
长青化工厂
公路80km
铁路150km
原料
产品
1.5元/(吨·千米)
1.2元/(吨·千米)
公路运费:15000元 铁路运费:97200元
长青化工厂用汽车从A地购买一批原料运回工厂,制成产品后用火车运到B地。工厂与A地相距80千米,与B地相距150千米。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输支出公路运费15000元,铁路运费97200元。求工厂从A地购得的原料有多少吨?制成的产品有多少吨?
合作探究
检鼠妈妈采松子,晴天每天可以采20个,雨天每天只能采12个,它一连共采了112个,平均每天采14个,问这几天当中有几天晴几天下雨?
据以往的统计资料,甲、乙两种作物的单位面积产量的比是1:1.5,现要在一块长200m,宽100m的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量的比是3:4(结果取整数)?
分析:如图所示,一种种植方案为:甲、乙两种作物的种植区域分别为长方形AEFD
和BCFE。设AE=xm,BE=ym,根据问题中涉及长度、产量的数量关系,列方程组
,
。
解这个方程组,得
x= ,
y= ,
过长方形土地的长边离一端约 处,把这块地分为两个长方形。较大一块地种 种作物,较小一块地种 种作物。
x
y
A
B
C
D
E
F
x+y=200
100x:1.5×100y=3:4
106m
甲种
乙种
1.《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何 ”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行.问人与车各多少 设有x人,y辆车,可列方程组为
中考链接
问题1 公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km)是什
么意思?
如:把2吨货物从A地运到100千米外的B地,
经公路运输需要支付:
公路运价:经公路运输1吨货物行驶1千米需1.5元
铁路运价:经铁路运输1吨货物行驶1千米需1.2元
1.5×2×100=300元,
1.2×2×100=240元
运输费 = 运价 × 质量 × 路程
经铁路运输需要支付:
合作探究
练一练:
1、两种枕木共300根,甲种枕木的总重量比乙种枕木的总重量轻1吨,如果每根枕木甲种重46千克,乙种重28千克,两种枕木各多少根?
2、蔬菜批发站有一批青菜分给两个学校的食堂,甲校食堂分得的5倍比乙校食堂分得的6倍少10kg;甲校食堂分得的3倍与乙校食堂分得的2倍的和是470kg。甲、乙两校食堂各分得青菜多少?
《九章算术》是中国传统数学的重要著作,方程术是它的最高成就.其中记载:今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?译文:今有人合伙购物,每人出8钱,会多3钱:每人出7钱,又会差4钱,问人数、物价各是多少?
中考链接
设产品为x吨,原料为y吨。
1.2·y ·120
1.5·y·10
1.5·x ·20
1.2·x ·110
运输费 = 运价 × 质量 × 路程
有大小两种货车,2辆大车与3辆小车
一次可以运货15.50吨,5辆大车与6辆小
车一次可以运货35吨。
求:3辆大车与5辆小车一次可以运货
多少吨
分析:要解决这个问题的关键是求每辆
大车和每辆小车一次可运货多少吨
解决此题的
关键是什么?
问题三
一艘轮船顺流航行45千米需要3小时,逆流航行65千米需要5小时,求船在静水中的速度和水流速度。
解:设船在静水中的速度为x千米/时,水流的速度为y千米/时,根据题意,得
答:船在静水中的速度及水流的速度分别为14千米/时、1千米/时.
解这个方程组得,
即
合作探究
例1:据以往的统计资料,甲、乙两种作物的单位面积产量的比
是 1:1.5,现要在一块长200m,宽100m的长方形土地上种
植这两种作物,怎样把这块地分为两个长方形,使甲、乙
两种作物的总产量的比是 3 : 4 (结果取整数)
A
B
C
D
甲种作物的总产量 = 甲的单位面积产量×甲的种植面积
乙种作物的总产量 = 乙的单位面积产量 ×乙的种植面积
同学们再见
