人教版数学七年级下册 8.3 实际问题与二元一次方程组 课件2(共22张PPT)
文档属性
| 名称 | 人教版数学七年级下册 8.3 实际问题与二元一次方程组 课件2(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 10:37:52 | ||
图片预览








文档简介
(共22张PPT)
实际问题与二元一次方程组
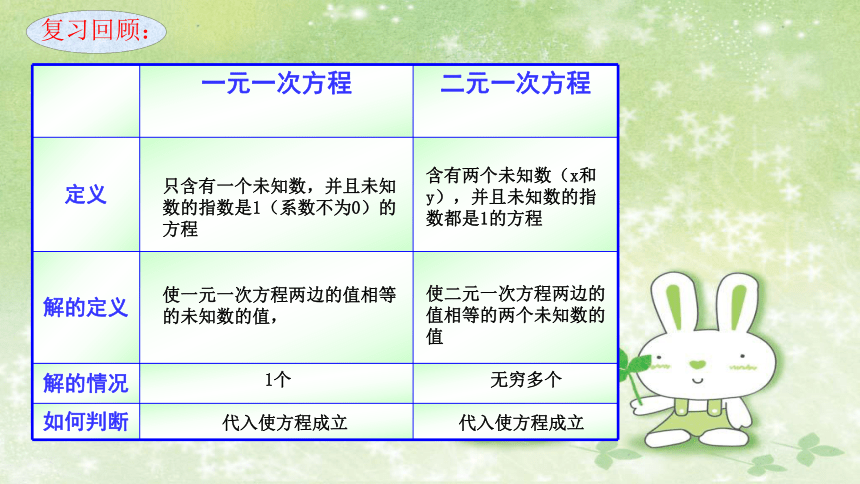
一元一次方程 二元一次方程
定义
解的定义
解的情况
如何判断
复习回顾:
只含有一个未知数,并且未知数的指数是1(系数不为0)的方程
含有两个未知数(x和y),并且未知数的指数都是1的方程
使一元一次方程两边的值相等的未知数的值,
使二元一次方程两边的值相等的两个未知数的值
1个
无穷多个
代入使方程成立
代入使方程成立
《数书九章》是南宋数学家秦九韶所著数学著作。书中共列算题81问,分为9类。全书采用问题集的形式,并按数学方法来分类。题文也不只谈数学,还涉及自然现象和社会生活,成为了解当时社会政治和经济生活的重要参考文献。
该书在数学内容上颇多创新,是对
《九章算术》的继承和发展。
它概括了宋元时期数学的主要成就,
标志着中国古代数学的高峰。
《数书九章》
养牛场原有30只大牛和15只小牛,1天约需要饲料675kg克;一周后又购进12只大牛和5只小牛,这时1天约需要饲料940kg。饲养员李大叔估计平均每只大牛1天约需饲料18至20kg,每只小牛1天约需要饲料7至8kg。请你通过计算检验李大叔的估计是否正确?
1、怎样检验他的估计呢?
2、题目中包含怎样的等量关系?
探究新知
问题:
篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队为了争取较好名次,想在全部16场比赛中得到28分,那么这个队胜负场数分别是多少
解:设平均每头大牛和每头小牛各约需饲料xkg和ykg.
根据题意,列方程组:
解这个方程组,得:
这就是说,平均每头大牛1天约需饲料20kg,每头小牛1天约需饲料5kg。饲养员李大叔对大牛的食量估计较准确,对小牛的食量估计偏高。
化简,得
探究新知
小华打字的速度是每分比小红多16个字,而小华2分钟内打的字比小红3分钟内打的字要少10个,问小华和小红的打字速度各是多少?
《算法统宗》甜果苦果问题
原文:九百九十九文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个 请君布算莫迟疑!
大意是说:用九百九十九文钱共买了一千个甜果和苦果,其中四文钱可以买苦果七个,十一文钱可
以买甜果九个,请问究竟甜、苦果各有几个
长青化工厂用汽车从A地购买一批原料运回工厂,
制成产品后用火车运到B地。工厂与A地相距80千米,
与B地相距150千米。公路运价为1.5元/(吨·千米),
铁路运价为1.2元/(吨·千米),这两次运输支出公路运费
15000元,铁路运费97200元。求工厂从A地购得的原料
有多少吨?制成的产品有多少吨?
分析:题中的量很多,并且相互关联,这时,我们可画一张示意图,把题中的条件在图中标出来,这样比较直,能帮助我们比较顺利地找出题中的相等关系。
合作探究
一船顺水航行45千米需要3小时,逆水航行65千米需要5小时,若设船在静水中的速度为x千米/小时,水流的速度为y㎞/h,则x、y的值为 ( ) A、X=3,y=2 B、x=14,y=1 C、x=15,y=1 E、x=14,y=2
B
《孙子算经》其中记载:
“今有木,不知长短,引绳度之,
余绳四尺五寸,屈绳量之,
不足一尺.木长几何?”
译文:“用一根绳子去量
一根长木,绳子还剩余4.5尺,
将绳子对折再量长木,长木还剩余1尺,
问木长多少尺?”
《九章算术》的“方程”这一章里,二元一次方程组是由算筹(算筹是中国古代用来记数、列式和进行演算的一种工具)来记录的.在算筹记数法中,以“立”“卧”两种排列方式来表示单位数目,表示两位数时,个位用立式,十位用卧式.如图(1),从左到右列出的算筹数分别表示x、y的系数与相应的常数项,根据图(1)可列出方程组
,则根据图(2)列出的
方程组 。
探究 如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地. 公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
合作探究
比一比:
班长为部分同学购买了以下两种面值的IP卡,共9张,花了330 元.你知道两种面值的IP卡各买了多少张吗?
根据题意列出二元一次方程组.
你能否判断两种面值的IP卡各买了多少张?
《九章算术》是我国古代数学的经典著作,奠定了中国传统数学的基本框架,书中记载:“今有大器五、小器一容三斛;大器一、小器五容二斛,问大小器各容几何?”译文:“今有大容器5个、小容器1个,总容量为3斛;大容器1个、小容器5个,总容量为2斛.问大小容器的容积各是多少斛?”设1个大容器的容积为x斛,1个小容器的容积y斛,则根据题意可列方程组为?
中考链接
问题4 这道题求的是什么?
这批产品的销售款比原料费与运输费的和多多少元?
问题5 要解决这个问题我们必须先知道什么?
销售款 原料费 运输费
销售款=产品单价×产品数量
原料费=原料单价×原料数量
运输费=铁路运费+公路运费
合作探究
某农场300名职工耕种51公顷土地,计划种植水稻、棉花和蔬菜,已知种植植物每公顷所需的劳动力人数及投入的资金如下表:
农作物品种 每公顷所需劳动力 每公顷投入资金
水稻 4人 1万元
棉花 8人 1万元
蔬菜 5人 2万元
已知农场计划在设备上投入67万元,应该怎样安排这三种作物的种植面积,才能使所有职工都有工作,而且投入的资金正好够用?
问题二
明代数学家程大位所著的《算法统宗》全称《直指算法统宗》,是中国古代数学名著.某数学兴趣小组发现《算法统宗》里有这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,共有50间客房.每间客房收费30钱,且每间客房最多入住3人,一次性定客房25间以上(含25间),房费按八折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
中考链接
解:设产品为x吨,原料为y吨,由题意得
解得:
销售款为:
8000×300=2400000(元)
原料费为:
1000×400=400000(元)
运输费为:
15000+97200=112200(元)
2400000-(400000+112200)=1887800(元)
答:销售款比原料费与运输费的和多1887800元。
1、有一艘船,载重量是800吨 , 容积是795立方米 , 现在要装运生铁和棉花两种物质,生铁每吨的体积是0.3立方米 , 棉花每吨的体积是4立方米 , 生铁和棉花各装多少 , 才能充分利用船的载重量和容积
2、有两种药水,一种浓度为60%,另一种浓度为90%,现要配制浓度为70%的药水300g,则每种各需多少克?
解决实际问题的基本过程
实际问题
设未知数、列方程(组)
数学问题
二元一次方程组
解方程
(组)
数学问题的解
二元一次方程组的解
检 验
实际问题的答案
建模
课堂小结
聪明出于勤奋,天才在于积累。
实际问题与二元一次方程组
一元一次方程 二元一次方程
定义
解的定义
解的情况
如何判断
复习回顾:
只含有一个未知数,并且未知数的指数是1(系数不为0)的方程
含有两个未知数(x和y),并且未知数的指数都是1的方程
使一元一次方程两边的值相等的未知数的值,
使二元一次方程两边的值相等的两个未知数的值
1个
无穷多个
代入使方程成立
代入使方程成立
《数书九章》是南宋数学家秦九韶所著数学著作。书中共列算题81问,分为9类。全书采用问题集的形式,并按数学方法来分类。题文也不只谈数学,还涉及自然现象和社会生活,成为了解当时社会政治和经济生活的重要参考文献。
该书在数学内容上颇多创新,是对
《九章算术》的继承和发展。
它概括了宋元时期数学的主要成就,
标志着中国古代数学的高峰。
《数书九章》
养牛场原有30只大牛和15只小牛,1天约需要饲料675kg克;一周后又购进12只大牛和5只小牛,这时1天约需要饲料940kg。饲养员李大叔估计平均每只大牛1天约需饲料18至20kg,每只小牛1天约需要饲料7至8kg。请你通过计算检验李大叔的估计是否正确?
1、怎样检验他的估计呢?
2、题目中包含怎样的等量关系?
探究新知
问题:
篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队为了争取较好名次,想在全部16场比赛中得到28分,那么这个队胜负场数分别是多少
解:设平均每头大牛和每头小牛各约需饲料xkg和ykg.
根据题意,列方程组:
解这个方程组,得:
这就是说,平均每头大牛1天约需饲料20kg,每头小牛1天约需饲料5kg。饲养员李大叔对大牛的食量估计较准确,对小牛的食量估计偏高。
化简,得
探究新知
小华打字的速度是每分比小红多16个字,而小华2分钟内打的字比小红3分钟内打的字要少10个,问小华和小红的打字速度各是多少?
《算法统宗》甜果苦果问题
原文:九百九十九文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个 请君布算莫迟疑!
大意是说:用九百九十九文钱共买了一千个甜果和苦果,其中四文钱可以买苦果七个,十一文钱可
以买甜果九个,请问究竟甜、苦果各有几个
长青化工厂用汽车从A地购买一批原料运回工厂,
制成产品后用火车运到B地。工厂与A地相距80千米,
与B地相距150千米。公路运价为1.5元/(吨·千米),
铁路运价为1.2元/(吨·千米),这两次运输支出公路运费
15000元,铁路运费97200元。求工厂从A地购得的原料
有多少吨?制成的产品有多少吨?
分析:题中的量很多,并且相互关联,这时,我们可画一张示意图,把题中的条件在图中标出来,这样比较直,能帮助我们比较顺利地找出题中的相等关系。
合作探究
一船顺水航行45千米需要3小时,逆水航行65千米需要5小时,若设船在静水中的速度为x千米/小时,水流的速度为y㎞/h,则x、y的值为 ( ) A、X=3,y=2 B、x=14,y=1 C、x=15,y=1 E、x=14,y=2
B
《孙子算经》其中记载:
“今有木,不知长短,引绳度之,
余绳四尺五寸,屈绳量之,
不足一尺.木长几何?”
译文:“用一根绳子去量
一根长木,绳子还剩余4.5尺,
将绳子对折再量长木,长木还剩余1尺,
问木长多少尺?”
《九章算术》的“方程”这一章里,二元一次方程组是由算筹(算筹是中国古代用来记数、列式和进行演算的一种工具)来记录的.在算筹记数法中,以“立”“卧”两种排列方式来表示单位数目,表示两位数时,个位用立式,十位用卧式.如图(1),从左到右列出的算筹数分别表示x、y的系数与相应的常数项,根据图(1)可列出方程组
,则根据图(2)列出的
方程组 。
探究 如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地. 公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
合作探究
比一比:
班长为部分同学购买了以下两种面值的IP卡,共9张,花了330 元.你知道两种面值的IP卡各买了多少张吗?
根据题意列出二元一次方程组.
你能否判断两种面值的IP卡各买了多少张?
《九章算术》是我国古代数学的经典著作,奠定了中国传统数学的基本框架,书中记载:“今有大器五、小器一容三斛;大器一、小器五容二斛,问大小器各容几何?”译文:“今有大容器5个、小容器1个,总容量为3斛;大容器1个、小容器5个,总容量为2斛.问大小容器的容积各是多少斛?”设1个大容器的容积为x斛,1个小容器的容积y斛,则根据题意可列方程组为?
中考链接
问题4 这道题求的是什么?
这批产品的销售款比原料费与运输费的和多多少元?
问题5 要解决这个问题我们必须先知道什么?
销售款 原料费 运输费
销售款=产品单价×产品数量
原料费=原料单价×原料数量
运输费=铁路运费+公路运费
合作探究
某农场300名职工耕种51公顷土地,计划种植水稻、棉花和蔬菜,已知种植植物每公顷所需的劳动力人数及投入的资金如下表:
农作物品种 每公顷所需劳动力 每公顷投入资金
水稻 4人 1万元
棉花 8人 1万元
蔬菜 5人 2万元
已知农场计划在设备上投入67万元,应该怎样安排这三种作物的种植面积,才能使所有职工都有工作,而且投入的资金正好够用?
问题二
明代数学家程大位所著的《算法统宗》全称《直指算法统宗》,是中国古代数学名著.某数学兴趣小组发现《算法统宗》里有这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,共有50间客房.每间客房收费30钱,且每间客房最多入住3人,一次性定客房25间以上(含25间),房费按八折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
中考链接
解:设产品为x吨,原料为y吨,由题意得
解得:
销售款为:
8000×300=2400000(元)
原料费为:
1000×400=400000(元)
运输费为:
15000+97200=112200(元)
2400000-(400000+112200)=1887800(元)
答:销售款比原料费与运输费的和多1887800元。
1、有一艘船,载重量是800吨 , 容积是795立方米 , 现在要装运生铁和棉花两种物质,生铁每吨的体积是0.3立方米 , 棉花每吨的体积是4立方米 , 生铁和棉花各装多少 , 才能充分利用船的载重量和容积
2、有两种药水,一种浓度为60%,另一种浓度为90%,现要配制浓度为70%的药水300g,则每种各需多少克?
解决实际问题的基本过程
实际问题
设未知数、列方程(组)
数学问题
二元一次方程组
解方程
(组)
数学问题的解
二元一次方程组的解
检 验
实际问题的答案
建模
课堂小结
聪明出于勤奋,天才在于积累。
