人教版数学七年级下册 9.1.1 不等式及其解集 课件(共17张PPT)
文档属性
| 名称 | 人教版数学七年级下册 9.1.1 不等式及其解集 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 946.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 15:57:45 | ||
图片预览





文档简介
(共17张PPT)
不等式及其解集
从图片中我们看到姚明的个头比小朋友高许多
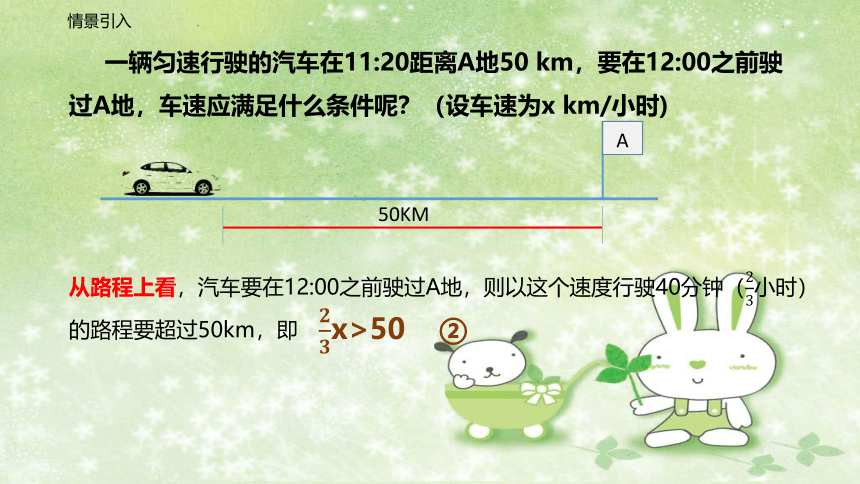
情景引入
一辆匀速行驶的汽车在11:20距离A地50 km,要在12:00之前驶过A地,车速应满足什么条件呢?(设车速为x km/小时)
A
50KM
从路程上看,汽车要在12:00之前驶过A地,则以这个速度行驶40分钟(小时)的路程要超过50km,即
x>50 ②
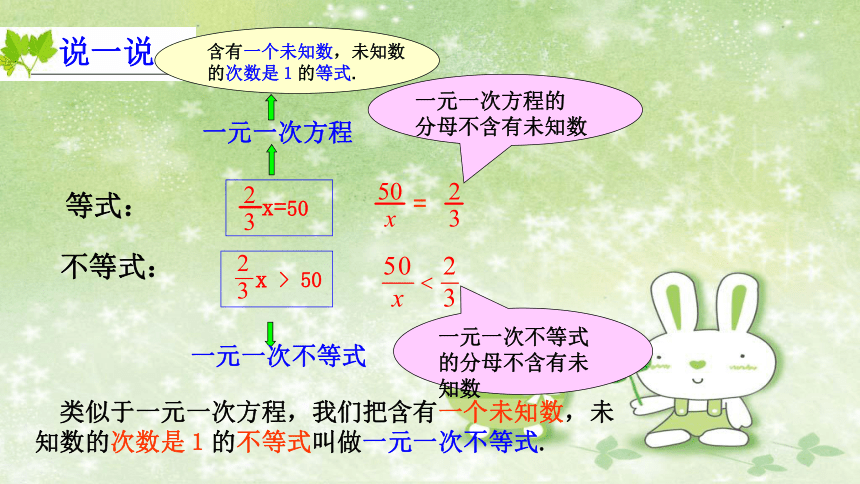
说一说
x=50
x > 50
=
等式:
不等式:
一元一次方程
一元一次方程的
分母不含有未知数
一元一次不等式
一元一次不等式的分母不含有未知数
含有一个未知数,未知数
的次数是1的等式.
类似于一元一次方程,我们把含有一个未知数,未知数的次数是1的不等式叫做一元一次不等式.
基础巩固
1、下列式子中哪些是不等式?
(1)7>5 (2)x +4>0 (3)4x +2x (4)x<5x+6 (5)2x=4x+5 (6)x +2x(9)3x-8<4x+1 (10)3a-17≤1
2、用不等式表示:
⑴ x与6的和是正数;
⑵ y的3倍与3的和小于7;
⑶ y的5倍与x的3倍的和是非负数;
x+6>0
3y+3<7
5y+3x≥0
欢乐岛
用我们的智慧来获取成功的喜悦!
过山车
摩天轮
旋转木马
旋转太阳伞
问题:
汽车到达A地的行驶能用多少时间呢?
11:20—12:00之间,汽车走过的实际路程是多少?
不等式的解集及解不等式
不等式的解集:一个含有未知数的不等式的所有解组成这个不等式的解集。(如x>75)
解不等式:求不等式的解集的过程。
用不等式表示下列数量关系:
(1)a是正数;
(2)x与5的和小于7;
(3)y的一半不小于3.
看我健笔如飞
不等式的概念:
不等式的符号统称不等号,有 “>” “<” “≠”, 其中“≤” “≥”也是不等号.
求不等式的解集
式子①x-y=2,②xy,③x+y,④x-3y,⑤ x≥0,⑥x3中,属于不等式的有( )
A.2个 B.3个 C.4个 D.5个
【详解】属于不等式的有:②⑤⑥.共3个,故选:B
1、看图写出不等式的解集:
.
x
0
-1.5
1.5
(1)
(2)
我思故我在
x
0
-4
4
2、用数轴表示下列不等式的解集:
⑴ x≥ -1 ; ⑵ x>-1; ⑶ x< -1; ⑷ x≤ -1.
总结: ①用数轴表示不等式的解集的步骤:
第一步:画数轴; 第二步:定界点; 第三步:定方向.
②用数轴表示不等式的解集,应记住下面的规律:
大于向右画,小于向左画;
有等号(≥ ,≤)画实心点,无等号(>,<)画空心圆.
关键词语 ①大 于 ②比…大③超 过 ①小 于 ②比…小③低 于 ①不大于 ②不超过 ③至 多 ①不小于 ②不低于 ③至 少 正数 负数 非负数 非正数
不等号
常用的表示不等关系的关键词语及对应的不等号
第一类:明确表明数量的不等关系
第二类:明确表明数量的范围特征
反思盘点 整合新知
>
<
≤
≥
>0
<0
≥0
≤0
利用数轴表示不等式的解决
用不等式表示如图的解集,其中正确的是( )
A. B.x≥2
C. D.x≤2
【解析】
解:根据“开口向左、实心”的特征可得解集为x≤2,故选D.
不等式的解集
一个含有未知数的不等式的所有的解,组成这个不等式的解集.
求不等式的解集的过程叫解不等式.
注:
(1)解集中包括了每一个解;
(2)解集是一个范围;
(3)解集中的任何一个数都是不等式的解. (4)解集中可能包括一个解,也可能包括无数解。
列不等式
下面列出的不等式中,正确的是( )
A.“m不是正数”表示为m<0
B.“m不大于2”表示为m<2
C.“n与4的差是负数”表示为n﹣4<0
D.“n不等于6”表示为n>6
【详解】
A. “m不是正数”表示为 故错误.
B. “m不大于2”表示为故错误.
C. “n与4的差是负数”表示为n﹣4<0,正确.
D. “n不等于6”表示为,故错误.故选:C.
聪明出于勤奋,天才在于积累。
不等式及其解集
从图片中我们看到姚明的个头比小朋友高许多
情景引入
一辆匀速行驶的汽车在11:20距离A地50 km,要在12:00之前驶过A地,车速应满足什么条件呢?(设车速为x km/小时)
A
50KM
从路程上看,汽车要在12:00之前驶过A地,则以这个速度行驶40分钟(小时)的路程要超过50km,即
x>50 ②
说一说
x=50
x > 50
=
等式:
不等式:
一元一次方程
一元一次方程的
分母不含有未知数
一元一次不等式
一元一次不等式的分母不含有未知数
含有一个未知数,未知数
的次数是1的等式.
类似于一元一次方程,我们把含有一个未知数,未知数的次数是1的不等式叫做一元一次不等式.
基础巩固
1、下列式子中哪些是不等式?
(1)7>5 (2)x +4>0 (3)4x +2x (4)x<5x+6 (5)2x=4x+5 (6)x +2x
2、用不等式表示:
⑴ x与6的和是正数;
⑵ y的3倍与3的和小于7;
⑶ y的5倍与x的3倍的和是非负数;
x+6>0
3y+3<7
5y+3x≥0
欢乐岛
用我们的智慧来获取成功的喜悦!
过山车
摩天轮
旋转木马
旋转太阳伞
问题:
汽车到达A地的行驶能用多少时间呢?
11:20—12:00之间,汽车走过的实际路程是多少?
不等式的解集及解不等式
不等式的解集:一个含有未知数的不等式的所有解组成这个不等式的解集。(如x>75)
解不等式:求不等式的解集的过程。
用不等式表示下列数量关系:
(1)a是正数;
(2)x与5的和小于7;
(3)y的一半不小于3.
看我健笔如飞
不等式的概念:
不等式的符号统称不等号,有 “>” “<” “≠”, 其中“≤” “≥”也是不等号.
求不等式的解集
式子①x-y=2,②xy,③x+y,④x-3y,⑤ x≥0,⑥x3中,属于不等式的有( )
A.2个 B.3个 C.4个 D.5个
【详解】属于不等式的有:②⑤⑥.共3个,故选:B
1、看图写出不等式的解集:
.
x
0
-1.5
1.5
(1)
(2)
我思故我在
x
0
-4
4
2、用数轴表示下列不等式的解集:
⑴ x≥ -1 ; ⑵ x>-1; ⑶ x< -1; ⑷ x≤ -1.
总结: ①用数轴表示不等式的解集的步骤:
第一步:画数轴; 第二步:定界点; 第三步:定方向.
②用数轴表示不等式的解集,应记住下面的规律:
大于向右画,小于向左画;
有等号(≥ ,≤)画实心点,无等号(>,<)画空心圆.
关键词语 ①大 于 ②比…大③超 过 ①小 于 ②比…小③低 于 ①不大于 ②不超过 ③至 多 ①不小于 ②不低于 ③至 少 正数 负数 非负数 非正数
不等号
常用的表示不等关系的关键词语及对应的不等号
第一类:明确表明数量的不等关系
第二类:明确表明数量的范围特征
反思盘点 整合新知
>
<
≤
≥
>0
<0
≥0
≤0
利用数轴表示不等式的解决
用不等式表示如图的解集,其中正确的是( )
A. B.x≥2
C. D.x≤2
【解析】
解:根据“开口向左、实心”的特征可得解集为x≤2,故选D.
不等式的解集
一个含有未知数的不等式的所有的解,组成这个不等式的解集.
求不等式的解集的过程叫解不等式.
注:
(1)解集中包括了每一个解;
(2)解集是一个范围;
(3)解集中的任何一个数都是不等式的解. (4)解集中可能包括一个解,也可能包括无数解。
列不等式
下面列出的不等式中,正确的是( )
A.“m不是正数”表示为m<0
B.“m不大于2”表示为m<2
C.“n与4的差是负数”表示为n﹣4<0
D.“n不等于6”表示为n>6
【详解】
A. “m不是正数”表示为 故错误.
B. “m不大于2”表示为故错误.
C. “n与4的差是负数”表示为n﹣4<0,正确.
D. “n不等于6”表示为,故错误.故选:C.
聪明出于勤奋,天才在于积累。
