4 圆周运动(共33张ppt)
文档属性
| 名称 | 4 圆周运动(共33张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-26 08:59:28 | ||
图片预览










文档简介
(共33张PPT)
4 圆周运动
时钟是我们生活中不可或缺的生活工具。时针和分针的尖端做什么运动?哪个针转动得快?你是根据什么比较的?
自行车的轮盘,飞轮,后轮上的质点,这些点运动得一样快吗?
2.理解什么是线速度、角速度和周期。
1.知道什么是匀速圆周运动。知道比较圆周运
动快慢的方法。
3.掌握线速度、角速度及周期之间的关系。
(难点)
(重点)
在物理学中,把质点的运动轨迹是圆或圆弧的运动叫做圆周运动。
【探究一:什么是圆周运动?】
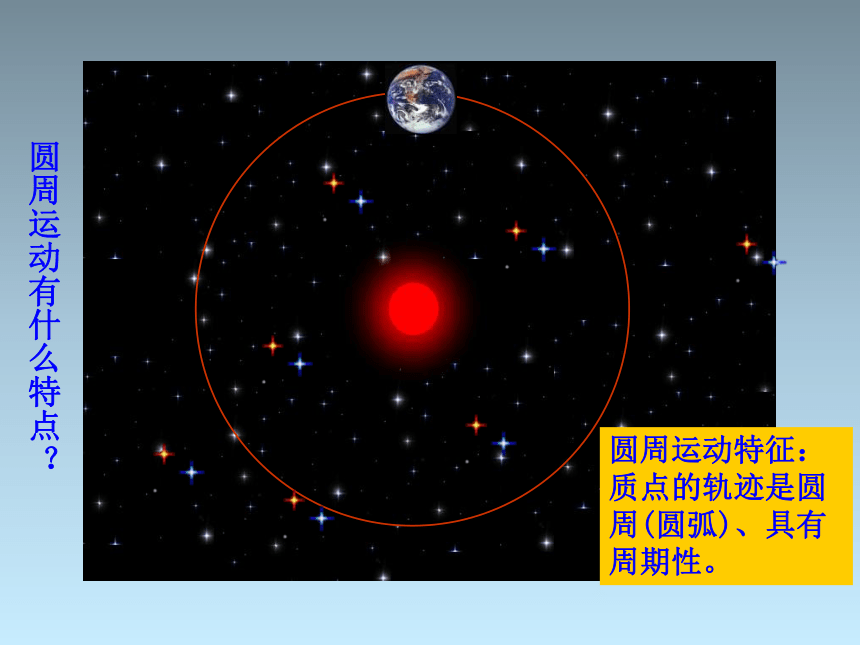
圆周运动特征:
质点的轨迹是圆周(圆弧)、具有周期性。
圆周运动有什么特点?
讨论:
如何描述自行车的链轮,飞轮和后轮运动快慢?
链轮
飞轮
后轮
【探究二:怎样描述圆周运动的快慢?】
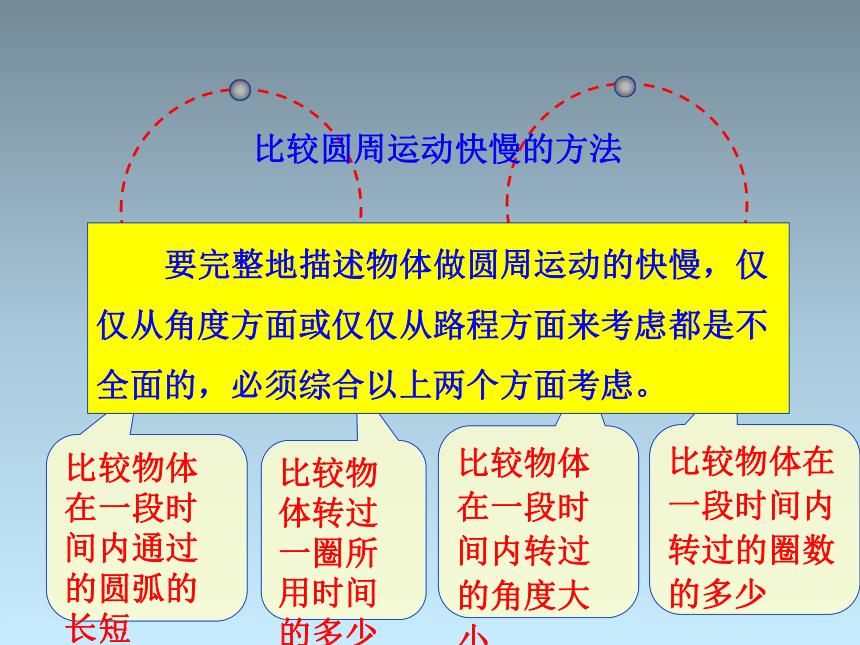
比较物体在一段时间内通过的圆弧的长短
比较物体在一段时间内转过的角度大小
比较物体转过一圈所用时间的多少
比较物体在一段时间内转过的圈数的多少
比较圆周运动快慢的方法
要完整地描述物体做圆周运动的快慢,仅 仅从角度方面或仅仅从路程方面来考虑都是不全面的,必须综合以上两个方面考虑。
1.物理意义:描述质点沿圆周运动的快慢。
矢量
探究三、圆周运动的线速度
2.定义:质点做圆周运动通过的弧长Δl和所用时间Δt 的比值叫做线速度。
3.线速度大小:
4.单位:m/s
v =
Δt
Δl
Δl是弧长还是位移?
当Δt 很小很小时(趋近零),弧长Δl 就等于物体的位移的大小,式中的v ,就是直线运动中学过的瞬时速度。
l
5.线速度方向:质点在圆周上某点的线速度方向就是沿圆周上该点的切线方向。
结合曲线运动知识,你知道
圆周运动的线速度方向吗?
任取两段相等的时间,比较通过的圆弧长度
6.匀速圆周运动
任意相等时间内通过的圆弧长度相等
(1)定义:物体沿着圆周运动,并且线速度的大小处处相等,这种运动叫做匀速圆周运动。
匀速圆周运动的“匀速”同“匀速直线运动”的“匀速”一样吗?
(2)匀速圆周运动的特点
v
v
v
o
注意匀速圆周运动是一 种变速曲线运动
速度方向在变化
速度方向有什么特点?
1.物理意义:描述质点转过圆心角的快慢。
2.定义:质点所在的半径转过的圆心角Δθ和所用时间Δt的比值叫做角速度。
3.大小:
4.单位:rad/s
Δ
θ
Δθ采用弧度制
说明:匀速圆周运动是角速度不变的运动。
探究四、匀速圆周运动的角速度
ω=
Δt
Δ
θ
探究五、匀速圆周运动的周期、频率和转速
2.频率f:做匀速圆周运动的物体1秒内沿圆周运动的周数。(单位:赫或Hz)
3.转速n:物体单位时间内转过的圈数。
单位:转/秒(r/s),或转/分(r/min)
1.周期T:做匀速圆周运动的物体转过一周所用的时间。(单位:秒)
4.线速度、角速度与周期的关系。
v =
T
2πr
(1)线速度与周期的关系:
(2)角速度与周期的关系:
ω=
T
2π
设物体做半径为 r 的匀速圆周运动:你能根据三者的定义推导出它们之间的关系吗?
拓展思考1:转速与角速度之间有怎样的关系?可以用什么表达式来表示?
当n的单位是r/s时
当n的单位是r/min时
角速度、周期、频率、转速
描述匀速圆周运动的各个物理量有哪些是恒定的?
拓展思考2
设物体做半径为r的匀速圆周运动,在Δt内通过的弧长为Δl ,半径转过的角度为Δθ。
由数学知识得Δl = rΔθ
v = = = rω
Δt
Δl
Δt
rΔ
θ
v = rω
l
Δ
θ
r
探究六、线速度与角速度的关系
拓展思考:
有没有其他推导方法?
结合 和
当v一定时,ω与r成反比
当ω一定时,v与r成正比
当r一定时,v与ω成正比
拓展思考:关于v=ωr的讨论:
根据上面的公式,得出速度v与角速度ω成正比,你同意这种说法吗?请说出你的理由。
归纳总结1:
(1)传动装置线速度的关系
a.皮带传动(不打滑,或链条传动)——边缘各点线速度大小相等
b.齿轮传动(或无齿,但不打滑)——线速度大小相等
归纳总结2:两个重要的结论
两红点处角速度有什么关系?
提示:同轴转动轮上各点的角速度相等。
同一轮上各点的角速度相同,周期相同
(2)同一轮上各点的角速度关系
【拓展思考】地球上的物体随着地球一起绕地轴自转。地球上不同纬度的物体的周期一样吗 角速度一样吗 线速度大小一样吗
O
R
θ
R'
O'
O
R
R'
θ
O'
【对点训练】如图所示的传动装置中,B、C 两轮固定在一起绕同一轴转动,A、B 两轮用皮带传动,三轮半径关系是rA=rC=2rB。若皮带不打滑,求A、B、C轮边缘的a、b、c三点的角速度之比和线速度之比。
【解析】A、B两轮通过皮带传动,皮带不打滑,则A、B两轮边缘的线速度大小相等,即va∶vb=1∶1 ①
由v=ωr得 ωa∶ωb=rB∶rA=1∶2 ②
B、C两轮固定在一起绕同一轴转动,则B、C两轮的角速度相同,即ωb=ωc(或ωb∶ωc=1∶1) ③
由v=ωr得 vb∶vc=rB∶rC=1∶2 ④
由②③得 ωa∶ωb∶ωc=1∶2∶2
由①④得 va∶vb∶vc=1∶1∶2
【解题关键】解这类题时要注意抓住传动装置的特点:
(1)同轴传动的是角速度相等,皮带传动是两轮边缘
的线速度大小相等。
(2)注意运用v=ωr找联系。
这里用到了哪
种物理思想?
物理量 大小 方向 物理意义
线速度
v v=s/t
v=2πr/T 沿圆弧的切线方向
表示质点沿圆弧运动的快慢
角速度 ω ω=θ/t ω=2π/T 不要求
周期T T=1/f 标量
频率f f=1/T 标量
转速n n=1/T 标量
1.做匀速圆周运动的物体,线速度 不变,
时刻在变,线速度是 (恒量或变
量),
匀速圆周运动的性质是 ,
匀速的含义是 。
大小
方向
变量
变速曲线运动
线速度的大小不变
2.(多选)对于做匀速圆周运动的物体,下列说法正
确的是( )
A.相等的时间里通过的路程相等
B.相等的时间里通过的弧长相等
C.相等的时间里发生的位移相同
D.相等的时间里转过的角度相等
ABD
3.机械手表的时针、分针、秒针的角速度之比为( )
A.1:60:360 B.1:12:360
C.1:12:720 D.1:60:7200
C
互动探究:时针和分针相邻两次两次重合
需要经过多长时间?是一个小时吗?
D
解题关键:
1.两地都在北半球但维度不同。
2.两物体随地球自转,角速度相同。
4.甲、乙两个物体分别放在广州和北京,它们随地
球一起转动时,下面说法正确的是( )
A.甲的线速度大,乙的角速度小
B.甲的线速度大,乙的角速度大
C.甲和乙的线速度相等
D.甲和乙的角速度相等
5. 如图所示,门上有A、B 两点,在开门过程中,A、B
两点的角速度、线速度大小关系是( )
A.ωA>ωB
B.ωA<ωB
C.vA>vB
D.vAC
不论做什么,请记住我的格言:笑容是良药,音乐是秘方,睡觉则可以让你忘掉一切。祝天天快乐!
4 圆周运动
时钟是我们生活中不可或缺的生活工具。时针和分针的尖端做什么运动?哪个针转动得快?你是根据什么比较的?
自行车的轮盘,飞轮,后轮上的质点,这些点运动得一样快吗?
2.理解什么是线速度、角速度和周期。
1.知道什么是匀速圆周运动。知道比较圆周运
动快慢的方法。
3.掌握线速度、角速度及周期之间的关系。
(难点)
(重点)
在物理学中,把质点的运动轨迹是圆或圆弧的运动叫做圆周运动。
【探究一:什么是圆周运动?】
圆周运动特征:
质点的轨迹是圆周(圆弧)、具有周期性。
圆周运动有什么特点?
讨论:
如何描述自行车的链轮,飞轮和后轮运动快慢?
链轮
飞轮
后轮
【探究二:怎样描述圆周运动的快慢?】
比较物体在一段时间内通过的圆弧的长短
比较物体在一段时间内转过的角度大小
比较物体转过一圈所用时间的多少
比较物体在一段时间内转过的圈数的多少
比较圆周运动快慢的方法
要完整地描述物体做圆周运动的快慢,仅 仅从角度方面或仅仅从路程方面来考虑都是不全面的,必须综合以上两个方面考虑。
1.物理意义:描述质点沿圆周运动的快慢。
矢量
探究三、圆周运动的线速度
2.定义:质点做圆周运动通过的弧长Δl和所用时间Δt 的比值叫做线速度。
3.线速度大小:
4.单位:m/s
v =
Δt
Δl
Δl是弧长还是位移?
当Δt 很小很小时(趋近零),弧长Δl 就等于物体的位移的大小,式中的v ,就是直线运动中学过的瞬时速度。
l
5.线速度方向:质点在圆周上某点的线速度方向就是沿圆周上该点的切线方向。
结合曲线运动知识,你知道
圆周运动的线速度方向吗?
任取两段相等的时间,比较通过的圆弧长度
6.匀速圆周运动
任意相等时间内通过的圆弧长度相等
(1)定义:物体沿着圆周运动,并且线速度的大小处处相等,这种运动叫做匀速圆周运动。
匀速圆周运动的“匀速”同“匀速直线运动”的“匀速”一样吗?
(2)匀速圆周运动的特点
v
v
v
o
注意匀速圆周运动是一 种变速曲线运动
速度方向在变化
速度方向有什么特点?
1.物理意义:描述质点转过圆心角的快慢。
2.定义:质点所在的半径转过的圆心角Δθ和所用时间Δt的比值叫做角速度。
3.大小:
4.单位:rad/s
Δ
θ
Δθ采用弧度制
说明:匀速圆周运动是角速度不变的运动。
探究四、匀速圆周运动的角速度
ω=
Δt
Δ
θ
探究五、匀速圆周运动的周期、频率和转速
2.频率f:做匀速圆周运动的物体1秒内沿圆周运动的周数。(单位:赫或Hz)
3.转速n:物体单位时间内转过的圈数。
单位:转/秒(r/s),或转/分(r/min)
1.周期T:做匀速圆周运动的物体转过一周所用的时间。(单位:秒)
4.线速度、角速度与周期的关系。
v =
T
2πr
(1)线速度与周期的关系:
(2)角速度与周期的关系:
ω=
T
2π
设物体做半径为 r 的匀速圆周运动:你能根据三者的定义推导出它们之间的关系吗?
拓展思考1:转速与角速度之间有怎样的关系?可以用什么表达式来表示?
当n的单位是r/s时
当n的单位是r/min时
角速度、周期、频率、转速
描述匀速圆周运动的各个物理量有哪些是恒定的?
拓展思考2
设物体做半径为r的匀速圆周运动,在Δt内通过的弧长为Δl ,半径转过的角度为Δθ。
由数学知识得Δl = rΔθ
v = = = rω
Δt
Δl
Δt
rΔ
θ
v = rω
l
Δ
θ
r
探究六、线速度与角速度的关系
拓展思考:
有没有其他推导方法?
结合 和
当v一定时,ω与r成反比
当ω一定时,v与r成正比
当r一定时,v与ω成正比
拓展思考:关于v=ωr的讨论:
根据上面的公式,得出速度v与角速度ω成正比,你同意这种说法吗?请说出你的理由。
归纳总结1:
(1)传动装置线速度的关系
a.皮带传动(不打滑,或链条传动)——边缘各点线速度大小相等
b.齿轮传动(或无齿,但不打滑)——线速度大小相等
归纳总结2:两个重要的结论
两红点处角速度有什么关系?
提示:同轴转动轮上各点的角速度相等。
同一轮上各点的角速度相同,周期相同
(2)同一轮上各点的角速度关系
【拓展思考】地球上的物体随着地球一起绕地轴自转。地球上不同纬度的物体的周期一样吗 角速度一样吗 线速度大小一样吗
O
R
θ
R'
O'
O
R
R'
θ
O'
【对点训练】如图所示的传动装置中,B、C 两轮固定在一起绕同一轴转动,A、B 两轮用皮带传动,三轮半径关系是rA=rC=2rB。若皮带不打滑,求A、B、C轮边缘的a、b、c三点的角速度之比和线速度之比。
【解析】A、B两轮通过皮带传动,皮带不打滑,则A、B两轮边缘的线速度大小相等,即va∶vb=1∶1 ①
由v=ωr得 ωa∶ωb=rB∶rA=1∶2 ②
B、C两轮固定在一起绕同一轴转动,则B、C两轮的角速度相同,即ωb=ωc(或ωb∶ωc=1∶1) ③
由v=ωr得 vb∶vc=rB∶rC=1∶2 ④
由②③得 ωa∶ωb∶ωc=1∶2∶2
由①④得 va∶vb∶vc=1∶1∶2
【解题关键】解这类题时要注意抓住传动装置的特点:
(1)同轴传动的是角速度相等,皮带传动是两轮边缘
的线速度大小相等。
(2)注意运用v=ωr找联系。
这里用到了哪
种物理思想?
物理量 大小 方向 物理意义
线速度
v v=s/t
v=2πr/T 沿圆弧的切线方向
表示质点沿圆弧运动的快慢
角速度 ω ω=θ/t ω=2π/T 不要求
周期T T=1/f 标量
频率f f=1/T 标量
转速n n=1/T 标量
1.做匀速圆周运动的物体,线速度 不变,
时刻在变,线速度是 (恒量或变
量),
匀速圆周运动的性质是 ,
匀速的含义是 。
大小
方向
变量
变速曲线运动
线速度的大小不变
2.(多选)对于做匀速圆周运动的物体,下列说法正
确的是( )
A.相等的时间里通过的路程相等
B.相等的时间里通过的弧长相等
C.相等的时间里发生的位移相同
D.相等的时间里转过的角度相等
ABD
3.机械手表的时针、分针、秒针的角速度之比为( )
A.1:60:360 B.1:12:360
C.1:12:720 D.1:60:7200
C
互动探究:时针和分针相邻两次两次重合
需要经过多长时间?是一个小时吗?
D
解题关键:
1.两地都在北半球但维度不同。
2.两物体随地球自转,角速度相同。
4.甲、乙两个物体分别放在广州和北京,它们随地
球一起转动时,下面说法正确的是( )
A.甲的线速度大,乙的角速度小
B.甲的线速度大,乙的角速度大
C.甲和乙的线速度相等
D.甲和乙的角速度相等
5. 如图所示,门上有A、B 两点,在开门过程中,A、B
两点的角速度、线速度大小关系是( )
A.ωA>ωB
B.ωA<ωB
C.vA>vB
D.vA
不论做什么,请记住我的格言:笑容是良药,音乐是秘方,睡觉则可以让你忘掉一切。祝天天快乐!
