苏科版九年级数学上册 3.1平均数(2)课件 (共15张PPT)
文档属性
| 名称 | 苏科版九年级数学上册 3.1平均数(2)课件 (共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 893.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
3.1 平均数(2)
忆一忆
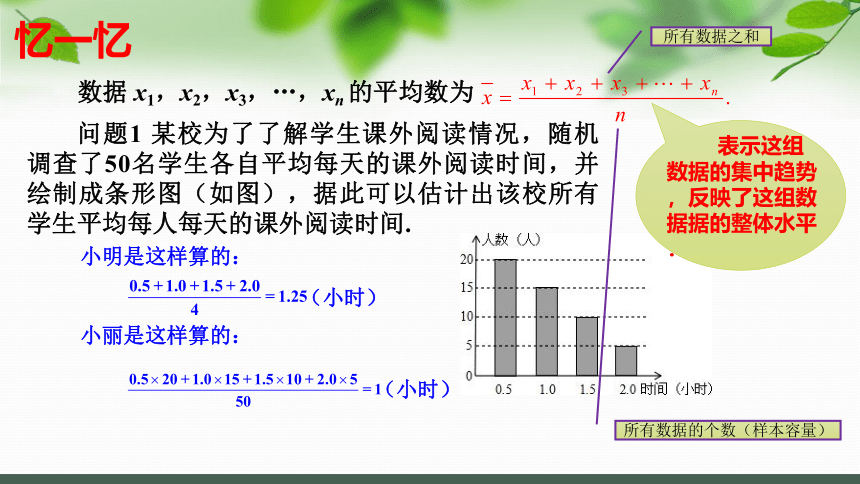
数据 x1,x2,x3,…,xn 的平均数为
表示这组数据的集中趋势,反映了这组数据据的整体水平.
问题1 某校为了了解学生课外阅读情况,随机调查了50名学生各自平均每天的课外阅读时间,并绘制成条形图(如图),据此可以估计出该校所有学生平均每人每天的课外阅读时间.
小明是这样算的:
(小时)
小丽是这样算的:
(小时)
所有数据之和
所有数据的个数(样本容量)
比一比
问题2 学校举办了一次英语竞赛,该竞赛由阅读、作文、听力和口语四部分构成,小明、小亮和小丽参加了这次竞赛,成绩如下:
阅读 作文 听力 口语
小明 90分 80分 80分 70分
小亮 80分 80分 70分 90分
小丽 70分 80分 90分 80分
(1)计算3个人4项比赛成绩的算术平均数,谁的竞赛成绩最高?
(2)根据这4项比赛成绩的“重要程度”,将阅读、作文、听力和口语分别按 3∶3∶2∶2 的比例计算他们3人的竞赛成绩,谁的竞赛成绩最高?
说一说
一组数据的平均数,不仅与这组数据中各个数据的值有关,而且与各个数据的“重要程度”有关.我们把衡量各个数据的“重要程度”的数值叫做权.
在第1个问题中,课外阅读时间0.5、1.0、1.5、2.0在平均数中的“重要程度”是不相同的,分别为20、15、10、5;在第2个问题中,阅读、作文、听力和口语成绩的“重要程度”分别是占“3、3、2和2”.
第 1 题中时间 0.5、1.0、1.5、2.0 的“权”分别是 ,
第 2 题中阅读、作文、听力和口语成绩的“权”分别是 .
小丽算得的平均数 1 小时是课外阅读时间的加权平均数.
学一学
一组数据中,数据 x1出现的次数(或权)为 f1,数据 x2出现的次数(或权)为 f2,数据 x3出现的次数(或权)为 f3, …,数据 xk出现的次数(或权)为 fk, 其中f1 + f2 + f3 + …+ fk=n ,则这组数据的平均数为:
例如:小明统计了15天同一时段通过某路口的汽车流量如下(单位:辆)
汽车流量 142 145 157 156
天数 2 2 5 6
求这15天在这个时段通过该路口的汽车平均流量.
142辆、145辆、157辆和156辆的权分别是多少?
公式中的 n 是多少?
所有数据之和
所有数据的个数(样本容量)
权的表现形式
1.用比表示的“权”
(1)某中学规定学生体育成绩满分为100分,按课外活动成绩、期中成绩、期末成绩2∶3∶5的比,计算学期成绩.小明同学本学期三项成绩依次为90分、90分、80分,则小明同学本学期的体育成绩是 分.
1.各数据的权分别是多少?
2.各数据的和是多少?
3.数据的个数(样本容量)是多少?
2.用百分比表示的“权”
(2)某校招聘教师,其中一名教师的笔试成绩是80分,面试成绩是60分,综合成绩笔试占60%,面试占40%,则该教师的综合成绩为 分.
权的表现形式
1.各数据的权分别是多少?
2.各数据的和是多少?
3.数据的个数(样本容量)是多少?
3.用频数(次数)表示的“权”
(3)为提升学生的自理和自立能力,李老师调查了全班学生在一周内的做饭次数情况,调查结果如下表:
一周做饭次数 4 5 6 7 8
人数 7 6 12 10 5
那么一周内该班学生的平均做饭次数为( )
A.4 B.5 C.6 D.7
权的表现形式
1.各数据的权分别是多少?
2.各数据的和是多少?
3.数据的个数(样本容量)是多少?
3.用频数(次数)表示的“权”
(4)为了解某班学生体育锻炼的用时情况,收集了该班学生一天用于体育锻炼的时间(单位:小时),整理成如图的统计图.则该班学生这天用于体育锻炼的平均时间为________小时.
权的表现形式
1.各数据的权分别是多少?
2.各数据的和是多少?
3.数据的个数(样本容量)是多少?
4.用频数(次数)表示组中的“权”
(5)对一组数据进行了整理,结果如下表:
权的表现形式
1.各数据的权分别是多少?
2.各数据的和是多少?
3.数据的个数(样本容量)是多少?
分组 0≤x<10 10≤x<20
频数 8 12
则这数据的平均数约是( )
A.10 B.11 C.12 D.16
∵ > ,
做一做
学校准备从甲、乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面进行了测试,他们各自的成绩(百分制)如下表:
选手 表达能力 阅读理解 综合素质 汉字听写
甲 85 78 85 73
乙 73 80 82 83
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁?
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2,1,3和4的权,请分别计算两位选手的平均成绩,从他们的这一成绩看,应选派谁?
解: (1)
∴应该选派甲.
(2)
∵ < ,
∴应该选派乙.
说一说
平均数
算术平均数
加权平均数
数据的集中趋势
做一做
1 .文明其精神,野蛮其体魄.体育课上张老师对全班学生进行了体能测试,从跑步、立定跳远、跳绳三个方面进行了量化考核.小宇和小彬的各项成绩如下表(百分制):
姓名 跑步 立定跳远 跳绳
小宇 85 95 90
小彬 95 86 88
若跑步、立定跳远、跳绳的成绩按 4∶3∶3 确定体能综合成绩,则小宇和小彬谁的体能综合成绩高?请通过计算说明理由.
做一做
2.某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛,现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录,甲、乙、丙三个小组各项得分如下表:
小组 研究报告 小组展示 答辩
甲 91 80 78
乙 81 74 85
丙 79 83 90
(1)计算各小组平均成绩;
(2)如果按照研究报告占40%,小组展示占30%,答辩占30%,计算各小组成绩,哪个小组的成绩最高?
同学们,再见!
3.1 平均数(2)
忆一忆
数据 x1,x2,x3,…,xn 的平均数为
表示这组数据的集中趋势,反映了这组数据据的整体水平.
问题1 某校为了了解学生课外阅读情况,随机调查了50名学生各自平均每天的课外阅读时间,并绘制成条形图(如图),据此可以估计出该校所有学生平均每人每天的课外阅读时间.
小明是这样算的:
(小时)
小丽是这样算的:
(小时)
所有数据之和
所有数据的个数(样本容量)
比一比
问题2 学校举办了一次英语竞赛,该竞赛由阅读、作文、听力和口语四部分构成,小明、小亮和小丽参加了这次竞赛,成绩如下:
阅读 作文 听力 口语
小明 90分 80分 80分 70分
小亮 80分 80分 70分 90分
小丽 70分 80分 90分 80分
(1)计算3个人4项比赛成绩的算术平均数,谁的竞赛成绩最高?
(2)根据这4项比赛成绩的“重要程度”,将阅读、作文、听力和口语分别按 3∶3∶2∶2 的比例计算他们3人的竞赛成绩,谁的竞赛成绩最高?
说一说
一组数据的平均数,不仅与这组数据中各个数据的值有关,而且与各个数据的“重要程度”有关.我们把衡量各个数据的“重要程度”的数值叫做权.
在第1个问题中,课外阅读时间0.5、1.0、1.5、2.0在平均数中的“重要程度”是不相同的,分别为20、15、10、5;在第2个问题中,阅读、作文、听力和口语成绩的“重要程度”分别是占“3、3、2和2”.
第 1 题中时间 0.5、1.0、1.5、2.0 的“权”分别是 ,
第 2 题中阅读、作文、听力和口语成绩的“权”分别是 .
小丽算得的平均数 1 小时是课外阅读时间的加权平均数.
学一学
一组数据中,数据 x1出现的次数(或权)为 f1,数据 x2出现的次数(或权)为 f2,数据 x3出现的次数(或权)为 f3, …,数据 xk出现的次数(或权)为 fk, 其中f1 + f2 + f3 + …+ fk=n ,则这组数据的平均数为:
例如:小明统计了15天同一时段通过某路口的汽车流量如下(单位:辆)
汽车流量 142 145 157 156
天数 2 2 5 6
求这15天在这个时段通过该路口的汽车平均流量.
142辆、145辆、157辆和156辆的权分别是多少?
公式中的 n 是多少?
所有数据之和
所有数据的个数(样本容量)
权的表现形式
1.用比表示的“权”
(1)某中学规定学生体育成绩满分为100分,按课外活动成绩、期中成绩、期末成绩2∶3∶5的比,计算学期成绩.小明同学本学期三项成绩依次为90分、90分、80分,则小明同学本学期的体育成绩是 分.
1.各数据的权分别是多少?
2.各数据的和是多少?
3.数据的个数(样本容量)是多少?
2.用百分比表示的“权”
(2)某校招聘教师,其中一名教师的笔试成绩是80分,面试成绩是60分,综合成绩笔试占60%,面试占40%,则该教师的综合成绩为 分.
权的表现形式
1.各数据的权分别是多少?
2.各数据的和是多少?
3.数据的个数(样本容量)是多少?
3.用频数(次数)表示的“权”
(3)为提升学生的自理和自立能力,李老师调查了全班学生在一周内的做饭次数情况,调查结果如下表:
一周做饭次数 4 5 6 7 8
人数 7 6 12 10 5
那么一周内该班学生的平均做饭次数为( )
A.4 B.5 C.6 D.7
权的表现形式
1.各数据的权分别是多少?
2.各数据的和是多少?
3.数据的个数(样本容量)是多少?
3.用频数(次数)表示的“权”
(4)为了解某班学生体育锻炼的用时情况,收集了该班学生一天用于体育锻炼的时间(单位:小时),整理成如图的统计图.则该班学生这天用于体育锻炼的平均时间为________小时.
权的表现形式
1.各数据的权分别是多少?
2.各数据的和是多少?
3.数据的个数(样本容量)是多少?
4.用频数(次数)表示组中的“权”
(5)对一组数据进行了整理,结果如下表:
权的表现形式
1.各数据的权分别是多少?
2.各数据的和是多少?
3.数据的个数(样本容量)是多少?
分组 0≤x<10 10≤x<20
频数 8 12
则这数据的平均数约是( )
A.10 B.11 C.12 D.16
∵ > ,
做一做
学校准备从甲、乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面进行了测试,他们各自的成绩(百分制)如下表:
选手 表达能力 阅读理解 综合素质 汉字听写
甲 85 78 85 73
乙 73 80 82 83
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁?
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2,1,3和4的权,请分别计算两位选手的平均成绩,从他们的这一成绩看,应选派谁?
解: (1)
∴应该选派甲.
(2)
∵ < ,
∴应该选派乙.
说一说
平均数
算术平均数
加权平均数
数据的集中趋势
做一做
1 .文明其精神,野蛮其体魄.体育课上张老师对全班学生进行了体能测试,从跑步、立定跳远、跳绳三个方面进行了量化考核.小宇和小彬的各项成绩如下表(百分制):
姓名 跑步 立定跳远 跳绳
小宇 85 95 90
小彬 95 86 88
若跑步、立定跳远、跳绳的成绩按 4∶3∶3 确定体能综合成绩,则小宇和小彬谁的体能综合成绩高?请通过计算说明理由.
做一做
2.某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛,现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录,甲、乙、丙三个小组各项得分如下表:
小组 研究报告 小组展示 答辩
甲 91 80 78
乙 81 74 85
丙 79 83 90
(1)计算各小组平均成绩;
(2)如果按照研究报告占40%,小组展示占30%,答辩占30%,计算各小组成绩,哪个小组的成绩最高?
同学们,再见!
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
