苏科版九年级上册3.4方差课件((共16张PPT))
文档属性
| 名称 | 苏科版九年级上册3.4方差课件((共16张PPT)) |

|
|
| 格式 | pptx | ||
| 文件大小 | 25.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
3.4 方差
创设情境1
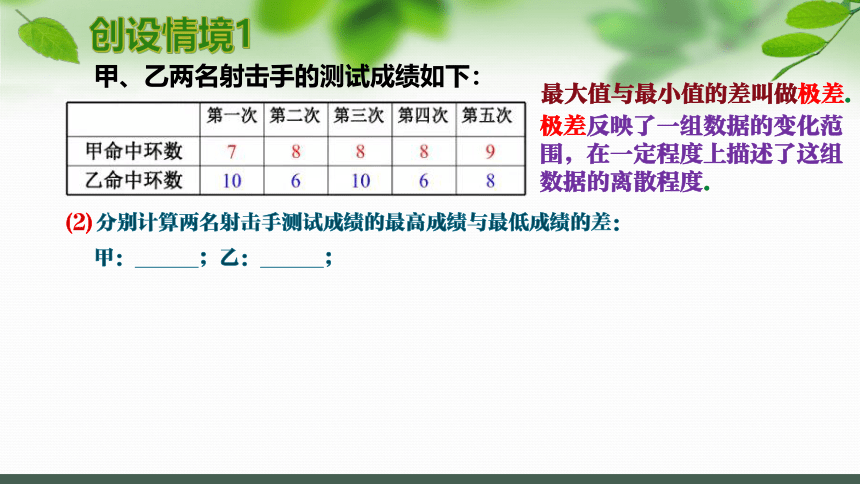
甲、乙两名射击手的测试成绩如下:
(1)分别计算两名射击手测试成绩的平均成绩为:
甲:______;乙:______;
现要从甲、乙两位射击手中选择一位参加比赛,如果你是教练,你觉得谁去参赛比较合适?
创设情境1
甲、乙两名射击手的测试成绩如下:
(2)分别计算两名射击手测试成绩的最高成绩与最低成绩的差:
甲:______;乙:______;
最大值与最小值的差叫做极差.
极差反映了一组数据的变化范围,在一定程度上描述了这组数据的离散程度.
创设情境1
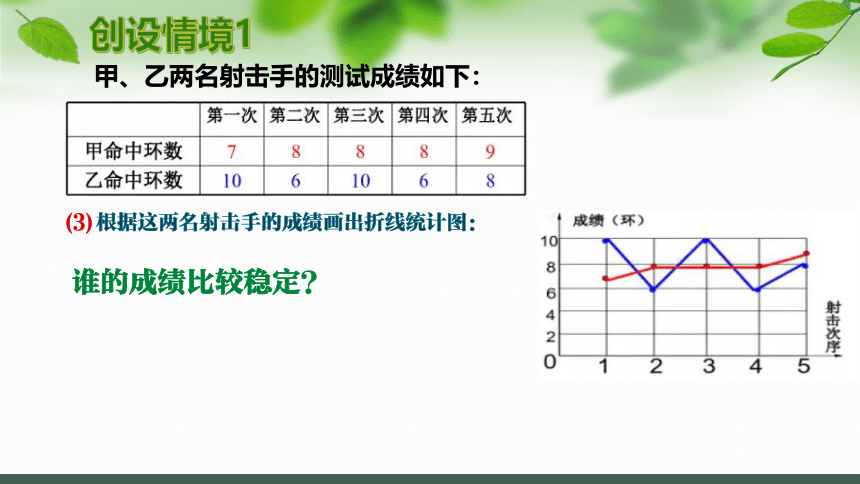
甲、乙两名射击手的测试成绩如下:
(3)根据这两名射击手的成绩画出折线统计图:
谁的成绩比较稳定?
创设情境2
甲、丙两名射击手的测试成绩如下:
如何比较这两组数据的离散程度呢?
谁的成绩比较稳定?
第一次 第二次 第三次 第四次 第五次
甲命中环数 7 8 8 8 9
丙命中环数 8 8 9 10 10
(1)分别计算两名射击手测试成绩的极差:
甲:______;丙:______;
创设情境2
甲、丙两名射击手的测试成绩如下:
第一次 第二次 第三次 第四次 第五次
甲命中环数 7 8 8 8 9
丙命中环数 8 8 9 10 10
(2)根据这两名射击手的测试成绩画出如下两幅图:
一组数据中的数与这组数据的平均数的偏离程度是数据的一个重要特征,它反映了一组数据的离散程度或波动大小.
创设情境2
甲、丙两名射击手的测试成绩如下:
第一次 第二次 第三次 第四次 第五次
甲命中环数 7 8 8 8 9
丙命中环数 8 8 9 10 10
(3)如何找到一个特征值来反映一组数据与其平均数的离散程度呢?
①先平均:
②再求差:
③后平方:
④再平均:
探究新知
设一组数据为x1,x2,…,xn,各数据与平均数 的差的平方的平均值,叫做这组数据的方差,记做 s2.
即
一般地,一组数据的方差越小,说明这组数据离散或波动的程度就越小,这组数据也就越稳定.
探究新知
甲、丙两名射击手的测试成绩如下:
第一次 第二次 第三次 第四次 第五次
甲命中环数 7 8 8 8 9
丙命中环数 8 8 9 10 10
(4)谁的成绩比较稳定呢?
一般地,一组数据的方差越小,说明这组数据离散或波动的程度就越小,这组数据也就越稳定.
典型例题
例1.有两个女声小合唱队,各由5名队员组成.她们的身高为(单位:cm)为:
甲队:160,162,159,160,159;
乙队:180,160,150,150,160.
如果单从队员的身高考虑,哪队的演出效果好?
解:甲队队员的平均身高是:
乙队队员的平均身高是:
甲队队员身高的方差是:
乙队队员身高的方差是:
计算的结果表明:乙队队员身高的方差比甲队队员身高的方差大很多,这说明乙队中各队员的身高波动大,而甲队中各队员的身高波动小,所以甲队队员的身高比较整齐,形象效果好.
典型例题
例2.为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子
钟中,各随机抽取5台进行测试,两种电子钟走时误差的数据如表(单位:s)
编号类型 一 二 三 四 五
甲种电子钟 1 -3 -4 4 2
乙种电子钟 4 -3 -1 2 -2
(1)计算甲、乙两种电子钟走时误差的极差;
(2)计算甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优.若两
种类型的电子钟价格相同,请问你买哪种电子钟 为什么
典型例题
例2.为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子
钟中,各随机抽取5台进行测试,两种电子钟走时误差的数据如表(单位:s)
编号类型 一 二 三 四 五
甲种电子钟 1 -3 -4 4 2
乙种电子钟 4 -3 -1 2 -2
(1)计算甲、乙两种电子钟走时误差的极差;
(2)计算甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优.若两
种类型的电子钟价格相同,请问你买哪种电子钟 为什么
巩固练习
1.根据甲、乙射击训练的成绩绘制了如图所示的折线统计图,根据下图提
供的信息,若要推荐一位成绩较稳定的选手去参赛,应推荐_______.
巩固练习
2.一组数据-3,-2,1,3,6,x的中位数为1,则极差为_____,方差为____.
巩固练习
3.已知数据x1,x2,…,xn的平均数是2,方差是1.3,则一组新数据3x1+5,
3x2+5,…,3xn+5的平均数是 ,方差是 .
课堂小结
1.经历刻画数据离散程度的探索过程,感受表示数据离散程度的必要性.
2.掌握极差、方差的概念,会计算一组数据的极差与方差,理解它们的
统计意义.
3.了解极差、方差是刻画数据离散程度的统计量,并在具体情境中加以
应用.
4.培养学生观察问题、分析问题的能力,培养学生的发散思维能力.
3.4 方差
创设情境1
甲、乙两名射击手的测试成绩如下:
(1)分别计算两名射击手测试成绩的平均成绩为:
甲:______;乙:______;
现要从甲、乙两位射击手中选择一位参加比赛,如果你是教练,你觉得谁去参赛比较合适?
创设情境1
甲、乙两名射击手的测试成绩如下:
(2)分别计算两名射击手测试成绩的最高成绩与最低成绩的差:
甲:______;乙:______;
最大值与最小值的差叫做极差.
极差反映了一组数据的变化范围,在一定程度上描述了这组数据的离散程度.
创设情境1
甲、乙两名射击手的测试成绩如下:
(3)根据这两名射击手的成绩画出折线统计图:
谁的成绩比较稳定?
创设情境2
甲、丙两名射击手的测试成绩如下:
如何比较这两组数据的离散程度呢?
谁的成绩比较稳定?
第一次 第二次 第三次 第四次 第五次
甲命中环数 7 8 8 8 9
丙命中环数 8 8 9 10 10
(1)分别计算两名射击手测试成绩的极差:
甲:______;丙:______;
创设情境2
甲、丙两名射击手的测试成绩如下:
第一次 第二次 第三次 第四次 第五次
甲命中环数 7 8 8 8 9
丙命中环数 8 8 9 10 10
(2)根据这两名射击手的测试成绩画出如下两幅图:
一组数据中的数与这组数据的平均数的偏离程度是数据的一个重要特征,它反映了一组数据的离散程度或波动大小.
创设情境2
甲、丙两名射击手的测试成绩如下:
第一次 第二次 第三次 第四次 第五次
甲命中环数 7 8 8 8 9
丙命中环数 8 8 9 10 10
(3)如何找到一个特征值来反映一组数据与其平均数的离散程度呢?
①先平均:
②再求差:
③后平方:
④再平均:
探究新知
设一组数据为x1,x2,…,xn,各数据与平均数 的差的平方的平均值,叫做这组数据的方差,记做 s2.
即
一般地,一组数据的方差越小,说明这组数据离散或波动的程度就越小,这组数据也就越稳定.
探究新知
甲、丙两名射击手的测试成绩如下:
第一次 第二次 第三次 第四次 第五次
甲命中环数 7 8 8 8 9
丙命中环数 8 8 9 10 10
(4)谁的成绩比较稳定呢?
一般地,一组数据的方差越小,说明这组数据离散或波动的程度就越小,这组数据也就越稳定.
典型例题
例1.有两个女声小合唱队,各由5名队员组成.她们的身高为(单位:cm)为:
甲队:160,162,159,160,159;
乙队:180,160,150,150,160.
如果单从队员的身高考虑,哪队的演出效果好?
解:甲队队员的平均身高是:
乙队队员的平均身高是:
甲队队员身高的方差是:
乙队队员身高的方差是:
计算的结果表明:乙队队员身高的方差比甲队队员身高的方差大很多,这说明乙队中各队员的身高波动大,而甲队中各队员的身高波动小,所以甲队队员的身高比较整齐,形象效果好.
典型例题
例2.为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子
钟中,各随机抽取5台进行测试,两种电子钟走时误差的数据如表(单位:s)
编号类型 一 二 三 四 五
甲种电子钟 1 -3 -4 4 2
乙种电子钟 4 -3 -1 2 -2
(1)计算甲、乙两种电子钟走时误差的极差;
(2)计算甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优.若两
种类型的电子钟价格相同,请问你买哪种电子钟 为什么
典型例题
例2.为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子
钟中,各随机抽取5台进行测试,两种电子钟走时误差的数据如表(单位:s)
编号类型 一 二 三 四 五
甲种电子钟 1 -3 -4 4 2
乙种电子钟 4 -3 -1 2 -2
(1)计算甲、乙两种电子钟走时误差的极差;
(2)计算甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优.若两
种类型的电子钟价格相同,请问你买哪种电子钟 为什么
巩固练习
1.根据甲、乙射击训练的成绩绘制了如图所示的折线统计图,根据下图提
供的信息,若要推荐一位成绩较稳定的选手去参赛,应推荐_______.
巩固练习
2.一组数据-3,-2,1,3,6,x的中位数为1,则极差为_____,方差为____.
巩固练习
3.已知数据x1,x2,…,xn的平均数是2,方差是1.3,则一组新数据3x1+5,
3x2+5,…,3xn+5的平均数是 ,方差是 .
课堂小结
1.经历刻画数据离散程度的探索过程,感受表示数据离散程度的必要性.
2.掌握极差、方差的概念,会计算一组数据的极差与方差,理解它们的
统计意义.
3.了解极差、方差是刻画数据离散程度的统计量,并在具体情境中加以
应用.
4.培养学生观察问题、分析问题的能力,培养学生的发散思维能力.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
