苏科版九年级上册4.2等可能条件下的概率课件(共18张PPT)
文档属性
| 名称 | 苏科版九年级上册4.2等可能条件下的概率课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
等可能条件下的概率(一)
情景引入
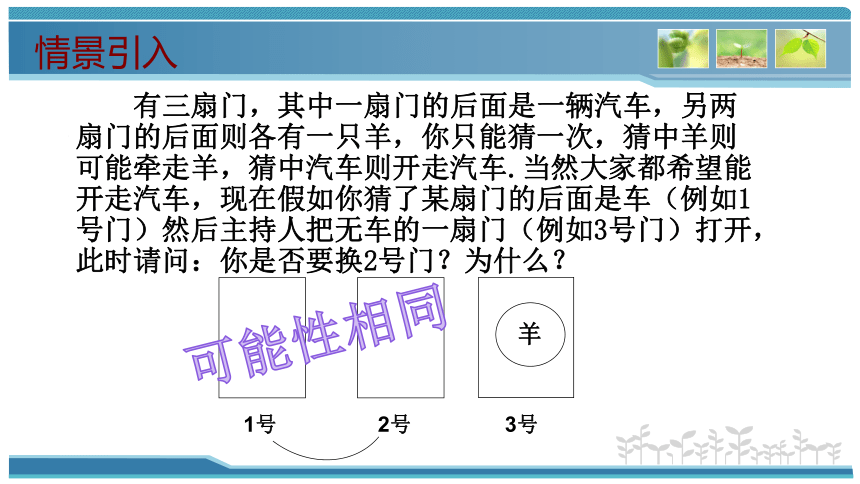
有三扇门,其中一扇门的后面是一辆汽车,另两扇门的后面则各有一只羊,你只能猜一次,猜中羊则可能牵走羊,猜中汽车则开走汽车.当然大家都希望能开走汽车,现在假如你猜了某扇门的后面是车(例如1号门)然后主持人把无车的一扇门(例如3号门)打开,此时请问:你是否要换2号门?为什么?
羊
1号
2号
3号
可能性相同
情景引入
抛掷一枚均匀的骰子一次.
(1)点数朝上的试验结果是有限的还是无限的?
如果是有限的共有几种?
(2)哪一个点数朝上的可能性较大?
(3)点数大于4与点数不大于4这两个事件中,哪个事件发生的可能性大呢?
因为骰子是均匀的,出现1、2、3、4、5、6点朝上,这6种结果是等可能的.
当朝上的点数是5或6点时,“朝上的点数大于4”这一事件(记为事件A)才能发生,所以事件A发生的概率为1/3.
当朝上的点数是1、2、3、4点时,“朝上的点数不大于4”这一事件(记为事件B)才能发生,所以事件B发生的概率为2/3.
∴出现“朝上的点数不大于4”比出现“朝上的点数大于4”的可能性大.
(3)朝上的点数大于4与点数不大于4这两个事件中,哪个事件发生的可能性大
情景引入
等可能条件下的概率的计算方法:
思考:
一般地,如果一个试验有n个等可能的结果,当其中的m个结果之一出现时,事件A发生,那么事件A发生的概率是多少呢?
归纳:
(其中m表示事件A发生可能出现的结果数,n表示一次试验所有等可能出现的结果数.)
新知归纳
小试牛刀
活动一
不透明的袋子甲中装有3个白球和2个红球.这些球除颜色外都相同,拌匀后从中任意出1个球.
(1)会出现哪些可能的结果?
(2)会出现哪些等可能的结果?
(3)摸出白球的概率是多少?
P (摸出白球)=
甲袋中装有3个白球和2个红球.乙袋中装有30个白球和20个红球.这些球除颜色外都相同,把两袋中的球都拌匀,从哪个袋中任意取出一个球恰好是红球的可能性大?
比一比
活动一
想一想
要使摸出的红球的概率是 0.5 ,则还需再加几个红球?
你还有其他方法吗?
小试牛刀
不透明的袋子甲中装有3个白球和2个红球.这些球除颜色外都相同,拌匀后从中任意出1个球.
(1)会出现哪些可能的结果?
(2)会出现哪些等可能的结果?
(3)摸出白球的概率是多少?
从一副扑克牌中,任意抽一张。问:
(1)抽到小王的概率是多少?
(2)抽到5的概率是多少?
(3)抽到方块的概率是多少?
(4)抽到方块5的概率是多少?
活动二
小试牛刀
1、如图所示,小区公园里有一块圆形地面被黑白石子铺成了面积相等的八部分,阴影部分是黑色石子,小华随意向其内部抛一个小球,则小球落在黑色石子区域内的概率是 .
练习巩固
0.5
2.我市民政部门近日举行了即开型社会福利彩票销售活动,设置彩票30000000张(每张彩票2元)在这些彩票中,设置如下的奖项.
奖项(万元) 50 15 8 4 ……
数量(个) 20 20 20 180 ……
如果花2元钱购买一张彩票,那么能得到不少于8万元大奖的概率是多少?
练习巩固
P(不少于8万元大奖)=
学以致用
B
C
D
B
D
C
C
B
D
C
D
B
D
B
C
D
C
B
解:所有可能出现的结果有六种,并且它们是等可能的.
1、一张圆桌旁有四个座位,A先坐在如图所示的座位上,B、C、D三人随机坐到其他三个座位上.求A与B不相邻而坐的概率.
学以致用
2、某校有A、B两个餐厅,甲、乙、丙三名学生各自随机选择其中的一个餐厅用餐.
(1)求甲、乙、丙三名学生在同一个餐厅用餐的概率;
(2)求三名学生中至少有一人在B餐厅用餐的概率.
解:按甲乙丙的顺序所有可能出现的结果是:
AAA,AAB,ABA, BAA, ABB,BAB,BBA,BBB
它们是等可能的.
3.“六一”期间,某游乐场举办一场活动,其中有一个游戏的规则如下:在一个装有8个红球和若干个白球(每个球除颜色外都相同)的袋子中,随机摸1个球,摸到红球就得到1个玩具.已知参加这种游戏的儿童有40000人,游乐场发放玩具8000个.
(1) 求参加该游戏得到玩具的概率;
学以致用
(2) 请你估计袋子中白球的个数.
P(参加该游戏得到玩具)=
由题意得,8÷0.2=40(个),40-8=32(个)
∴袋子中白球的个数为32个.
能力提升
问题1 一个不透明的袋子中装有红、黄、白三种颜色的球共100个,它们除颜色外都相同,其中黄球的个数比白球个数的2倍还多5个.已知从袋子中摸出一个球是红球的概率是0.2 .
∴P(从袋子中摸出1个球是白球)=
∵100×0.2=20(个)∴袋子中红球的个数为20个.
(1) 求袋子中红球的个数;
(2) 求从袋子中摸出1个球是白球的概率;
∵设白球有x个,可得方程:20+x+2x+5=100,解得x=25.
能力提升
问题1 一个不透明的袋子中装有红、黄、白三种颜色的球共100个,它们除颜色外都相同,其中黄球的个数比白球个数的2倍还多5个.已知从袋子中摸出一个球是红球的概率是0.2 .
∴P(从袋子中摸出1个球是红球)=
(3) 取走20个球(其中有4个红球)后,求从剩余的球中摸出一个球是红球的概率.
(4) 取走20个球后,如果要使摸到红球的概率变为 ,需再往袋子里加入 个红球.
48
能力提升
问题2 五张正面分别标有数-2、0、1、3、5的不透明卡片,它们除数不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,将该卡片上的数记为m.求数字m使分式方程 无解的概率.
解:
∵分式方程无解
∴ x =1 或 x =-2
即 m =3 或 m=0
∴P(数字m使分式方程无解)=
课堂小结
回忆一下,这节课我们学到了什么!
事件A发生可能出现的结果数
一次试验的所有等可能出现的结果数
P(A)=
m
n
一般地,如果一个试验有n个等可能的结果,当其中的m个结果之一出现时,事件A发生,那么事件A发生的概率记为P(A)
感谢你的陪伴!
下次再见!
等可能条件下的概率(一)
情景引入
有三扇门,其中一扇门的后面是一辆汽车,另两扇门的后面则各有一只羊,你只能猜一次,猜中羊则可能牵走羊,猜中汽车则开走汽车.当然大家都希望能开走汽车,现在假如你猜了某扇门的后面是车(例如1号门)然后主持人把无车的一扇门(例如3号门)打开,此时请问:你是否要换2号门?为什么?
羊
1号
2号
3号
可能性相同
情景引入
抛掷一枚均匀的骰子一次.
(1)点数朝上的试验结果是有限的还是无限的?
如果是有限的共有几种?
(2)哪一个点数朝上的可能性较大?
(3)点数大于4与点数不大于4这两个事件中,哪个事件发生的可能性大呢?
因为骰子是均匀的,出现1、2、3、4、5、6点朝上,这6种结果是等可能的.
当朝上的点数是5或6点时,“朝上的点数大于4”这一事件(记为事件A)才能发生,所以事件A发生的概率为1/3.
当朝上的点数是1、2、3、4点时,“朝上的点数不大于4”这一事件(记为事件B)才能发生,所以事件B发生的概率为2/3.
∴出现“朝上的点数不大于4”比出现“朝上的点数大于4”的可能性大.
(3)朝上的点数大于4与点数不大于4这两个事件中,哪个事件发生的可能性大
情景引入
等可能条件下的概率的计算方法:
思考:
一般地,如果一个试验有n个等可能的结果,当其中的m个结果之一出现时,事件A发生,那么事件A发生的概率是多少呢?
归纳:
(其中m表示事件A发生可能出现的结果数,n表示一次试验所有等可能出现的结果数.)
新知归纳
小试牛刀
活动一
不透明的袋子甲中装有3个白球和2个红球.这些球除颜色外都相同,拌匀后从中任意出1个球.
(1)会出现哪些可能的结果?
(2)会出现哪些等可能的结果?
(3)摸出白球的概率是多少?
P (摸出白球)=
甲袋中装有3个白球和2个红球.乙袋中装有30个白球和20个红球.这些球除颜色外都相同,把两袋中的球都拌匀,从哪个袋中任意取出一个球恰好是红球的可能性大?
比一比
活动一
想一想
要使摸出的红球的概率是 0.5 ,则还需再加几个红球?
你还有其他方法吗?
小试牛刀
不透明的袋子甲中装有3个白球和2个红球.这些球除颜色外都相同,拌匀后从中任意出1个球.
(1)会出现哪些可能的结果?
(2)会出现哪些等可能的结果?
(3)摸出白球的概率是多少?
从一副扑克牌中,任意抽一张。问:
(1)抽到小王的概率是多少?
(2)抽到5的概率是多少?
(3)抽到方块的概率是多少?
(4)抽到方块5的概率是多少?
活动二
小试牛刀
1、如图所示,小区公园里有一块圆形地面被黑白石子铺成了面积相等的八部分,阴影部分是黑色石子,小华随意向其内部抛一个小球,则小球落在黑色石子区域内的概率是 .
练习巩固
0.5
2.我市民政部门近日举行了即开型社会福利彩票销售活动,设置彩票30000000张(每张彩票2元)在这些彩票中,设置如下的奖项.
奖项(万元) 50 15 8 4 ……
数量(个) 20 20 20 180 ……
如果花2元钱购买一张彩票,那么能得到不少于8万元大奖的概率是多少?
练习巩固
P(不少于8万元大奖)=
学以致用
B
C
D
B
D
C
C
B
D
C
D
B
D
B
C
D
C
B
解:所有可能出现的结果有六种,并且它们是等可能的.
1、一张圆桌旁有四个座位,A先坐在如图所示的座位上,B、C、D三人随机坐到其他三个座位上.求A与B不相邻而坐的概率.
学以致用
2、某校有A、B两个餐厅,甲、乙、丙三名学生各自随机选择其中的一个餐厅用餐.
(1)求甲、乙、丙三名学生在同一个餐厅用餐的概率;
(2)求三名学生中至少有一人在B餐厅用餐的概率.
解:按甲乙丙的顺序所有可能出现的结果是:
AAA,AAB,ABA, BAA, ABB,BAB,BBA,BBB
它们是等可能的.
3.“六一”期间,某游乐场举办一场活动,其中有一个游戏的规则如下:在一个装有8个红球和若干个白球(每个球除颜色外都相同)的袋子中,随机摸1个球,摸到红球就得到1个玩具.已知参加这种游戏的儿童有40000人,游乐场发放玩具8000个.
(1) 求参加该游戏得到玩具的概率;
学以致用
(2) 请你估计袋子中白球的个数.
P(参加该游戏得到玩具)=
由题意得,8÷0.2=40(个),40-8=32(个)
∴袋子中白球的个数为32个.
能力提升
问题1 一个不透明的袋子中装有红、黄、白三种颜色的球共100个,它们除颜色外都相同,其中黄球的个数比白球个数的2倍还多5个.已知从袋子中摸出一个球是红球的概率是0.2 .
∴P(从袋子中摸出1个球是白球)=
∵100×0.2=20(个)∴袋子中红球的个数为20个.
(1) 求袋子中红球的个数;
(2) 求从袋子中摸出1个球是白球的概率;
∵设白球有x个,可得方程:20+x+2x+5=100,解得x=25.
能力提升
问题1 一个不透明的袋子中装有红、黄、白三种颜色的球共100个,它们除颜色外都相同,其中黄球的个数比白球个数的2倍还多5个.已知从袋子中摸出一个球是红球的概率是0.2 .
∴P(从袋子中摸出1个球是红球)=
(3) 取走20个球(其中有4个红球)后,求从剩余的球中摸出一个球是红球的概率.
(4) 取走20个球后,如果要使摸到红球的概率变为 ,需再往袋子里加入 个红球.
48
能力提升
问题2 五张正面分别标有数-2、0、1、3、5的不透明卡片,它们除数不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,将该卡片上的数记为m.求数字m使分式方程 无解的概率.
解:
∵分式方程无解
∴ x =1 或 x =-2
即 m =3 或 m=0
∴P(数字m使分式方程无解)=
课堂小结
回忆一下,这节课我们学到了什么!
事件A发生可能出现的结果数
一次试验的所有等可能出现的结果数
P(A)=
m
n
一般地,如果一个试验有n个等可能的结果,当其中的m个结果之一出现时,事件A发生,那么事件A发生的概率记为P(A)
感谢你的陪伴!
下次再见!
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
