沪科版数学八年级下册 勾股定理(4)-课件(共19张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 勾股定理(4)-课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 11:17:51 | ||
图片预览





文档简介
(共19张PPT)
18.1 勾 股 定 理
问题是数学的心脏
创设情境,引入新课
2002年世界数学大会在北京召开,本次大会的会徽是赵爽弦图
探索新知
毕达哥拉斯
毕达哥拉斯(约公元前580~前500)生于萨摩斯他是希腊著名哲学家、数学家,天文学家.有次应邀参加一位富有政要的餐会,发现朋友家的地砖很有规律,引起他的关注
探索新知
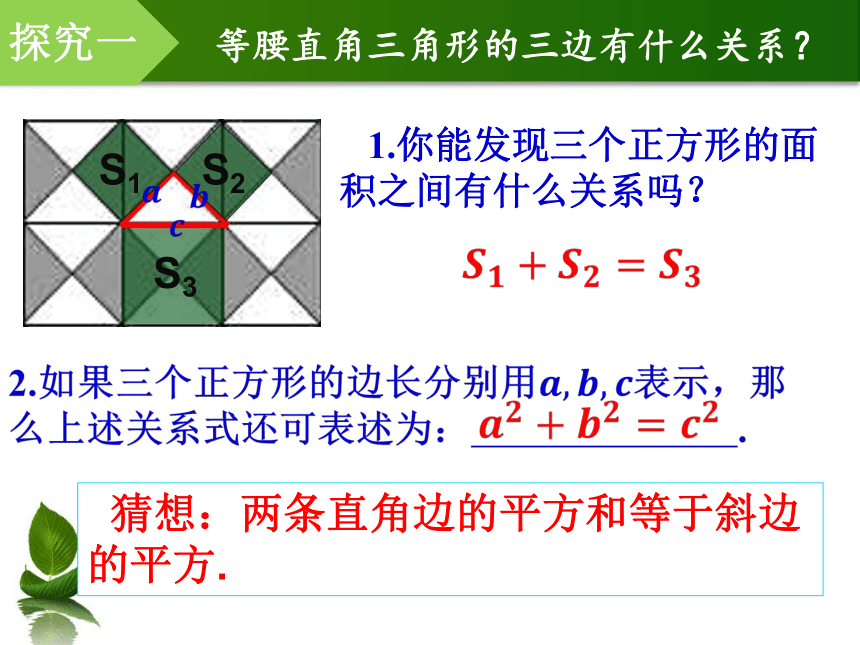
S1
S2
S3
探究一
等腰直角三角形的三边有什么关系?
1.你能发现三个正方形的面积之间有什么关系吗?
猜想:两条直角边的平方和等于斜边的平方.
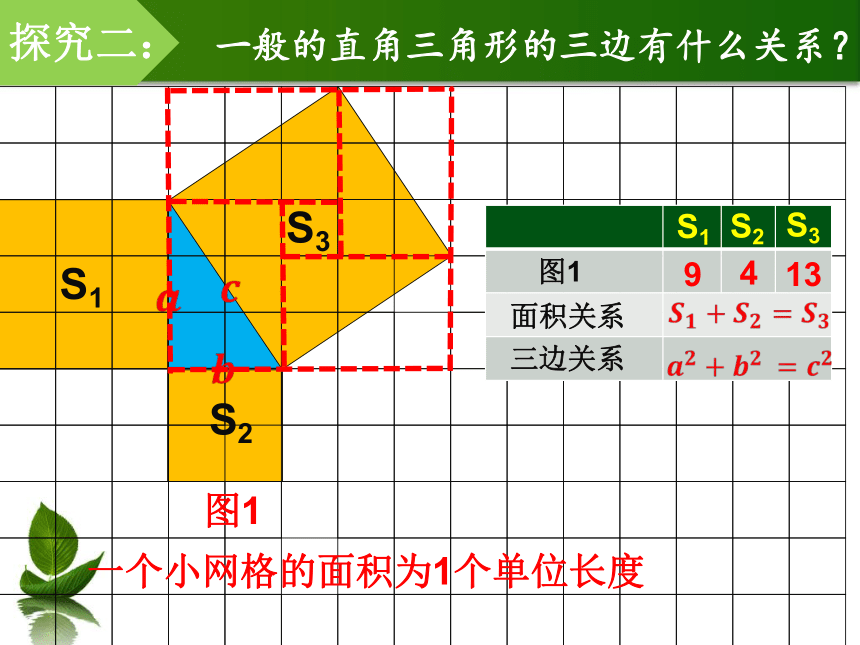
探究二:
一般的直角三角形的三边有什么关系?
S1
S2
S3
图1
一个小网格的面积为1个单位长度
图1
S1
S2
S3
面积关系
三边关系
9
4
13
如何证明?
命题:直角三角形两条直角边的平方和等于斜边的平方.
猜一猜:
直角三角形的三边有什么关系?
a
a
b
b
=
+
+
+
(a+b)2
a2
ab
ab
b2
经典再现
= a2+2ab+b2
思考:能不能类比这种方法来证明勾股定理呢?
拼一拼
(1)你能用四个全等的直角三角形拼成一
个正方形吗?
(2)你能表示出大正方形的面积吗?
证一证:
赵爽弦图
勾股定理
符号语言:如果直角三角形两直角边分别为a,b,
斜边为c,那么
文字语言:直角三角形两直角边的平方和等于斜边的平方.
a
c
b
(毕达哥拉斯定理)
说一说
勾
股
弦
1、在Rt△ABC中,如果两条直角边的长
分别为3和4,求第三边长?
变式1:Rt△ABC中,已知两条边长分别
为3和4,求第三边长?
小试牛刀
小试牛刀
1、在Rt△ABC中,如果两条直角边的长
分别为3和4,求第三边长?
变式1:Rt△ABC中,已知两条边长分别
为3和4,求第三边长?
变式2:在三角形中,已知两边边长是3和4,你能求出第三边的长吗?
小试牛刀
分别以Rt △ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,容易得出S1、S2、S3之间有的关系式为 .
经典再现
妙变勾股图
如果我们分别以Rt△ABC的三边为边(或直径),向外画三个正三角形(或半圆),那么这三个正三角形(或半圆)的面积之间又有什么样的关系?
课堂小结
本节课你有什么收获?
应用面积法证明勾股定理
2 勾股定理的简单应用
3 数学方法:转化思想,分类讨论和数形结合
作业布置
必做题:课本57页习题18.1
第1题 第2题
选做题: 第3题
寄语
数学中一些美丽定理具有这样的特性:它们极易从事实中归纳出来,但证明却隐藏的很深,我们要有一双善于观察的双眼和一颗爱思考的大脑!加油,孩子们!
18.1 勾 股 定 理
问题是数学的心脏
创设情境,引入新课
2002年世界数学大会在北京召开,本次大会的会徽是赵爽弦图
探索新知
毕达哥拉斯
毕达哥拉斯(约公元前580~前500)生于萨摩斯他是希腊著名哲学家、数学家,天文学家.有次应邀参加一位富有政要的餐会,发现朋友家的地砖很有规律,引起他的关注
探索新知
S1
S2
S3
探究一
等腰直角三角形的三边有什么关系?
1.你能发现三个正方形的面积之间有什么关系吗?
猜想:两条直角边的平方和等于斜边的平方.
探究二:
一般的直角三角形的三边有什么关系?
S1
S2
S3
图1
一个小网格的面积为1个单位长度
图1
S1
S2
S3
面积关系
三边关系
9
4
13
如何证明?
命题:直角三角形两条直角边的平方和等于斜边的平方.
猜一猜:
直角三角形的三边有什么关系?
a
a
b
b
=
+
+
+
(a+b)2
a2
ab
ab
b2
经典再现
= a2+2ab+b2
思考:能不能类比这种方法来证明勾股定理呢?
拼一拼
(1)你能用四个全等的直角三角形拼成一
个正方形吗?
(2)你能表示出大正方形的面积吗?
证一证:
赵爽弦图
勾股定理
符号语言:如果直角三角形两直角边分别为a,b,
斜边为c,那么
文字语言:直角三角形两直角边的平方和等于斜边的平方.
a
c
b
(毕达哥拉斯定理)
说一说
勾
股
弦
1、在Rt△ABC中,如果两条直角边的长
分别为3和4,求第三边长?
变式1:Rt△ABC中,已知两条边长分别
为3和4,求第三边长?
小试牛刀
小试牛刀
1、在Rt△ABC中,如果两条直角边的长
分别为3和4,求第三边长?
变式1:Rt△ABC中,已知两条边长分别
为3和4,求第三边长?
变式2:在三角形中,已知两边边长是3和4,你能求出第三边的长吗?
小试牛刀
分别以Rt △ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,容易得出S1、S2、S3之间有的关系式为 .
经典再现
妙变勾股图
如果我们分别以Rt△ABC的三边为边(或直径),向外画三个正三角形(或半圆),那么这三个正三角形(或半圆)的面积之间又有什么样的关系?
课堂小结
本节课你有什么收获?
应用面积法证明勾股定理
2 勾股定理的简单应用
3 数学方法:转化思想,分类讨论和数形结合
作业布置
必做题:课本57页习题18.1
第1题 第2题
选做题: 第3题
寄语
数学中一些美丽定理具有这样的特性:它们极易从事实中归纳出来,但证明却隐藏的很深,我们要有一双善于观察的双眼和一颗爱思考的大脑!加油,孩子们!
