沪科版数学八年级下册 18.1勾股定理-课件(共14张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 18.1勾股定理-课件(共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 12:05:26 | ||
图片预览



文档简介
(共14张PPT)
18.1 勾股定理
1
1
美丽的勾股数
一
一 创设情境
除地球外,别的星球上有没有生命呢?
自古以来,人类就不断发出这样的疑问,特别是
近年来不断出现UFO事件,更让人相信有外星人的
说法。如果真的有,那我们怎么和他们交流呢?
我国著名的数学家华罗庚在多年前曾提出这样的
设想:向太空发射一种图形,因为这种图形在几千
年前就已经被人类认识.到底是一种什么样的图形
呢?
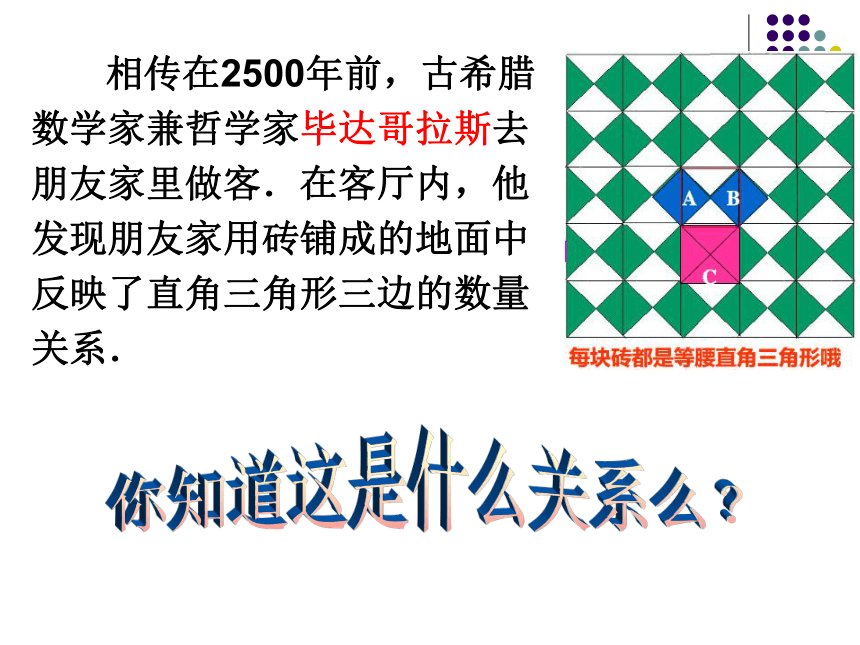
相传在2500年前,古希腊
数学家兼哲学家毕达哥拉斯去
朋友家里做客.在客厅内,他
发现朋友家用砖铺成的地面中
反映了直角三角形三边的数量
关系.
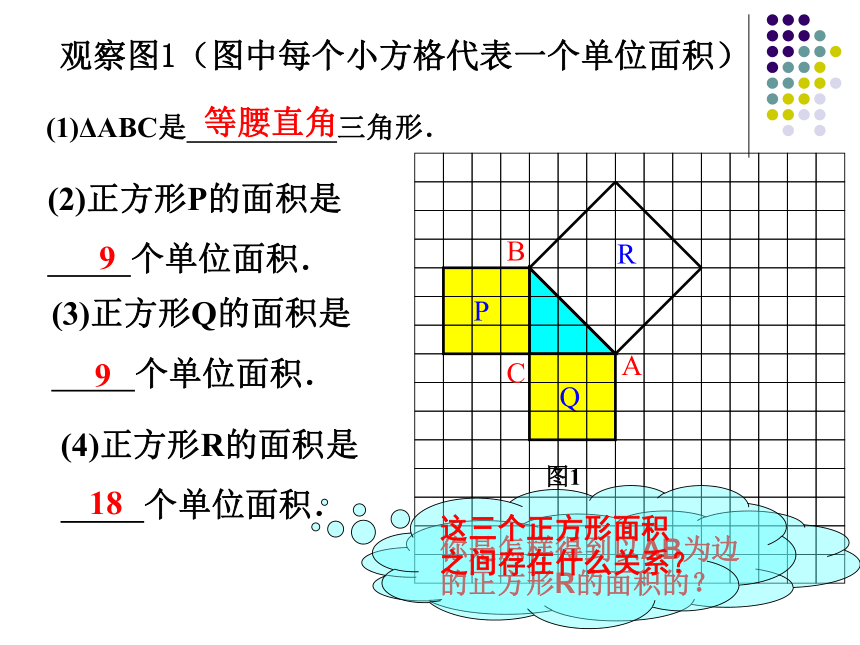
观察图1(图中每个小方格代表一个单位面积)
P
Q
R
图1
(2)正方形P的面积是
个单位面积.
(3)正方形Q的面积是
个单位面积.
(4)正方形R的面积是
个单位面积.
9
18
你是怎样得到以AB为边的正方形R的面积的?
9
B
C
A
(1)ΔABC是 三角形.
等腰直角
这三个正方形面积之间存在什么关系?
c
4
3
I
C
A
B
D
E
H
G
F
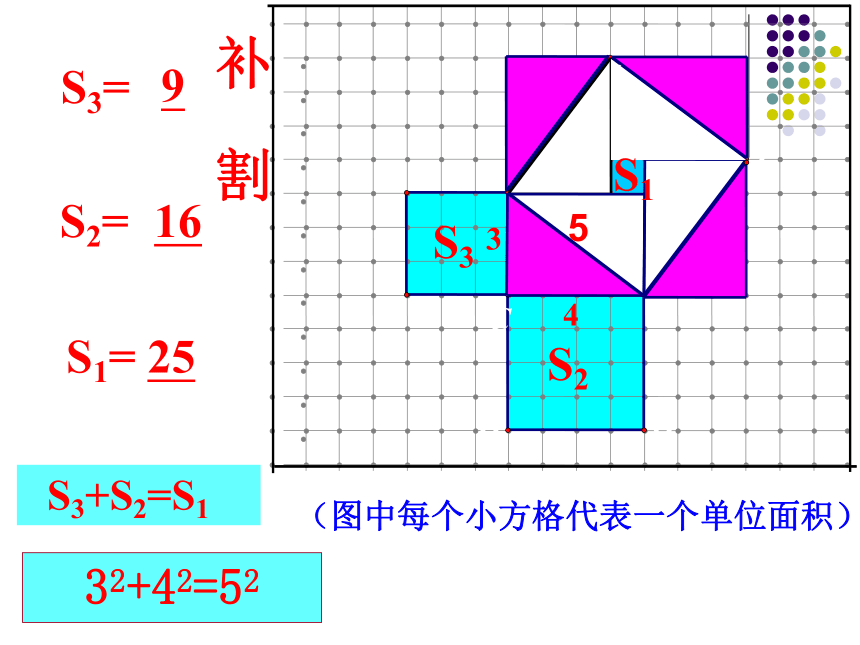
S3=
S2=
S1=
9
16
25
S3+S2=S1
(图中每个小方格代表一个单位面积)
补
割
5
32+42=52
S3
S2
S1
勾股定理(毕达哥拉斯定理)
(gou-gu theorem)
如果直角三角形两直角边分别为a, b,斜边为c,那么
即直角三角形两直角边的平方和等于 斜边的平方.
a
c
勾
弦
b
股
二 讲授新知
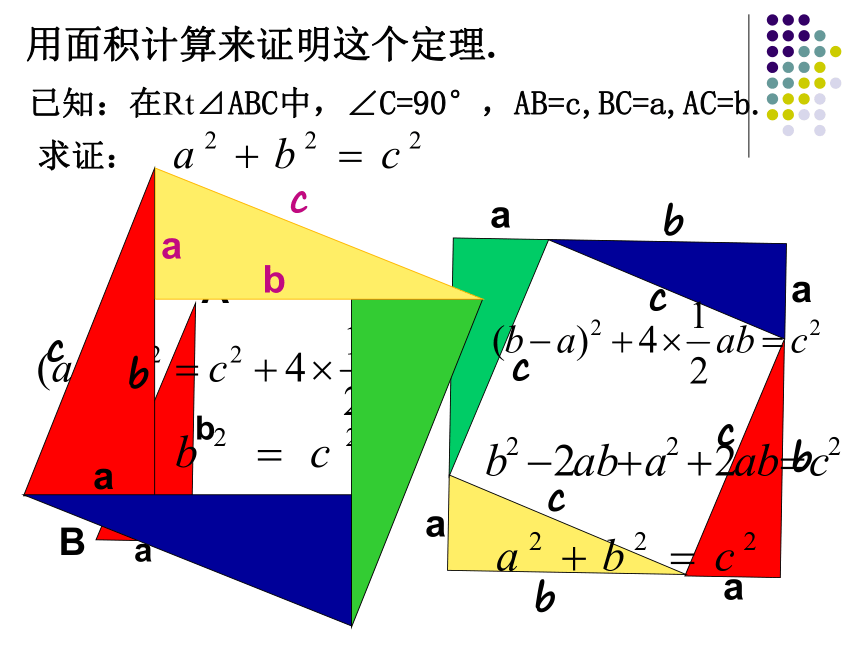
用面积计算来证明这个定理.
已知:在Rt⊿ABC中,∠C=90°,AB=c,BC=a,AC=b.
求证:
A
C
B
a
b
c
a
b
c
a
b
c
a
a
b
b
c
c
a
c
b
a
b
c
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。
1881年,伽菲尔德就任美国第20任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”。
1、判断:
(1)若a、b、c是三角形的三边,则a2+b2=c2。
(2)若a、b是直角三角形的两条直角边,c为斜边,
则a2=c2 -b2 。
(3)若a、b、c是直角三角形的三边,则a2+b2=c2
2、填空:
在直角三角形ABC中, ∠C=90°,AB=c,BC=a,AC=b。
1)已知a=9,b=12,则c= 。
2)已知a=3,c=5, 则b= 。
c
b
a
A
B
C
×
×
√
三 小试牛刀
15
4
1.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
15
5
7
如果一个直角三角形的两条边长分别是3厘米和4厘米,那么这个三角形的周长是多少厘米?
3
4
3
4
解 (1)当这两条边是直角边时,斜边长
为 .所以周长为
3+4+5=12(厘米).
(2)当一条直角边长为3厘米,斜边长
为4厘米时,另一条直角边为
.所以周长为
(厘米).
四 课堂小结
①本节课学到了什么数学知识?
②你了解了勾股定理的发现方法了吗?
③你还有什么困惑?
五 布置作业
教材第55页习题18.1第1、2、3题
1
1
美丽的勾股树
18.1 勾股定理
1
1
美丽的勾股数
一
一 创设情境
除地球外,别的星球上有没有生命呢?
自古以来,人类就不断发出这样的疑问,特别是
近年来不断出现UFO事件,更让人相信有外星人的
说法。如果真的有,那我们怎么和他们交流呢?
我国著名的数学家华罗庚在多年前曾提出这样的
设想:向太空发射一种图形,因为这种图形在几千
年前就已经被人类认识.到底是一种什么样的图形
呢?
相传在2500年前,古希腊
数学家兼哲学家毕达哥拉斯去
朋友家里做客.在客厅内,他
发现朋友家用砖铺成的地面中
反映了直角三角形三边的数量
关系.
观察图1(图中每个小方格代表一个单位面积)
P
Q
R
图1
(2)正方形P的面积是
个单位面积.
(3)正方形Q的面积是
个单位面积.
(4)正方形R的面积是
个单位面积.
9
18
你是怎样得到以AB为边的正方形R的面积的?
9
B
C
A
(1)ΔABC是 三角形.
等腰直角
这三个正方形面积之间存在什么关系?
c
4
3
I
C
A
B
D
E
H
G
F
S3=
S2=
S1=
9
16
25
S3+S2=S1
(图中每个小方格代表一个单位面积)
补
割
5
32+42=52
S3
S2
S1
勾股定理(毕达哥拉斯定理)
(gou-gu theorem)
如果直角三角形两直角边分别为a, b,斜边为c,那么
即直角三角形两直角边的平方和等于 斜边的平方.
a
c
勾
弦
b
股
二 讲授新知
用面积计算来证明这个定理.
已知:在Rt⊿ABC中,∠C=90°,AB=c,BC=a,AC=b.
求证:
A
C
B
a
b
c
a
b
c
a
b
c
a
a
b
b
c
c
a
c
b
a
b
c
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。
1881年,伽菲尔德就任美国第20任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”。
1、判断:
(1)若a、b、c是三角形的三边,则a2+b2=c2。
(2)若a、b是直角三角形的两条直角边,c为斜边,
则a2=c2 -b2 。
(3)若a、b、c是直角三角形的三边,则a2+b2=c2
2、填空:
在直角三角形ABC中, ∠C=90°,AB=c,BC=a,AC=b。
1)已知a=9,b=12,则c= 。
2)已知a=3,c=5, 则b= 。
c
b
a
A
B
C
×
×
√
三 小试牛刀
15
4
1.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
15
5
7
如果一个直角三角形的两条边长分别是3厘米和4厘米,那么这个三角形的周长是多少厘米?
3
4
3
4
解 (1)当这两条边是直角边时,斜边长
为 .所以周长为
3+4+5=12(厘米).
(2)当一条直角边长为3厘米,斜边长
为4厘米时,另一条直角边为
.所以周长为
(厘米).
四 课堂小结
①本节课学到了什么数学知识?
②你了解了勾股定理的发现方法了吗?
③你还有什么困惑?
五 布置作业
教材第55页习题18.1第1、2、3题
1
1
美丽的勾股树
