华师大版数学八年级上册同步课件:11.1.2 立方根(共19张PPT)
文档属性
| 名称 | 华师大版数学八年级上册同步课件:11.1.2 立方根(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 328.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 12:21:26 | ||
图片预览






文档简介
(共19张PPT)
11.1 2. 立方根
(1)什么叫一个数a的平方根?如何用符号表示数a(a≥0)的平方根?
(2)正数的平方根有几个?它们之间的关系是什么?负数有没有平方根?0的平方根是什么?
正数的平方根有两个,它们之间互为相反数,负数没有平方根,0的平方根是0.
x2=a,x=
知识回顾
(3)平方和开平方运算有何关系?
(4)算术平方根和平方根有何区别与联系?
互逆的过程
一个正数的算术平方根只有一个,而平方根有两个,互为相反数;0的算术平方根和平方根都是0;负数没有算术平方根也没有平方根;算术平方根是平方根中的正值部分.
要做一只容积为216 cm3的正方体纸盒,
正方体的棱长是多少?
这个实际问题,在数学上可以转化成一个怎样的计算问题?从中可以抽象出一个什么数学概念?
类比“平方根”定义,给出你的推测.
情景导入
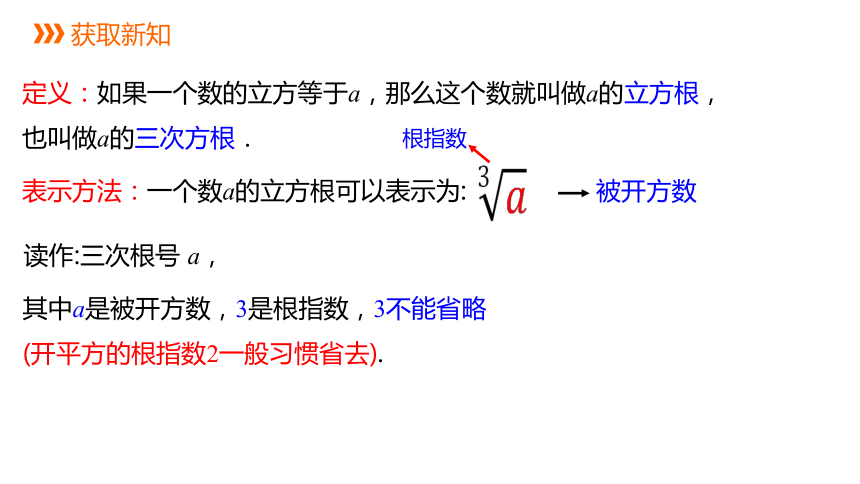
定义:如果一个数的立方等于a,那么这个数就叫做a的立方根,也叫做a的三次方根.
表示方法:一个数a的立方根可以表示为:
根指数
被开方数
其中a是被开方数,3是根指数,3不能省略
(开平方的根指数2一般习惯省去).
读作:三次根号 a,
获取新知
如果正方体的体积为5cm3,正方体的边长又该是多少?
解:设正方体的边长为x,则
所以正方体的边长是
求一个数的立方根的运算,叫做开立方.
立方
开立方
互逆
到现在我们学了几种运算
+,-,×,÷,乘方,开方(开平方,开立方)
求立方根的方法:若x3=a ,则 =x;也就是说找出立方等于a的数即为a的平方根。
-27
2
27
0
0.1
通过这些题目的解答,你能看出正数、0、负数的
立方根各有什么特点
怎样求下列括号内的数 各题中已知什么数 求什么数
(1)( )3=0.001; (2)( )3=- ;
(3)( )3=0; (4)33=( );
(5)( )3=8; (6)(-3)3=( ).
(2)利用 可以把求一个负数的立方根
转化为求一个正数的立方根的相反数.
立方根性质:
(1)正数的立方根是正数;
(2)负数的立方根是负数;
(3)0的立方根是0;
(4);
要点精析:
(1) 互为相反数的数的立方根也互为相反数;
规律:对于任何数a都有
2
-2
-3
4
0
计算下面各题,你能发现什么规律?
规律:对于任何数a都有
8
-8
27
-27
0
计算下面各题,你能发现什么规律?
平方根和立方根的异同点
被开方数 平方根 立方根
有两个互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
正数
负数
零
立方根是它本身的数有那些
有1, -1, 0
平方根是它本身的数呢
只有0
例1 求下列各数的立方根.
(1) ;(2)-125;(3)-0.008.
(2) 因为(-5) =-125,
即 =-5.
(3)因为(-0.2)3=-0.008,
所以 .
解:(1) 因为
所以
求一个负数的立方根,可以先求出这个负数绝对值的立方根,然后再取它的相反数.
例题讲解
说明:用计算器求一个有理数的立方根,只需直接按书写顺序按键即可.
例2 用计算器求下列各数的立方根:
(1)1331 ; (2)9.263(精确到0.01).
解:(1)在计算器上依次键入:
显示结果为11,所以
3
3
1
SHIFT
=
1
(2)在计算器上依次键入:
显示结果为 2.1001511606987 ,要求精确到0.01,可得
2.10
9
.
2
6
3
=
SHIFT
1. 64的立方根为( )
A.4 B.±4 C.8 D.±8
A
2.下列说法正确的是( )
A.0.8的立方根是0.2
B.1的立方根为±1
C.-1的立方根是-1
D.-25没有立方根
C
随堂演练
3.求下列各式的值:
(1) ; (2) ; (3) ; (4) .
4.因为(____)3=-27,所以-27的立方根是________,用数学式子表示为__________;因为(______)3=0,所以0的立方根是________,用数学式子表示为________;因为(______)3=8,所以8的立方根是________,用数学式子表示为________.
-3
-3
0
0
2
2
5.已知:x-2的平方根是±2,2x+y+7的立方根是3,
求x2+y2的算术平方根.
解:因为x-2的平方根是±2,
所以x-2=4. 所以x=6.
因为2x+y+7的立方根是3,
所以2x+y+7=27.
把x=6代入解得:y=8,
所以x2+y2=62+82=100.
所以x2+y2的算术平方根为10.
都是开方运算的结果.
平方根与立方根
正数有两个平方根,它们互为相反数;负数没有平方根.
主要区别:
正数有一个立方根,仍为正数;负数有一个立方根,仍为负数.
联系:
非负数都有平方根和立方根;0的平方根和立方根都是0.
课堂小结
(1)
(2)
(1)
(2)
11.1 2. 立方根
(1)什么叫一个数a的平方根?如何用符号表示数a(a≥0)的平方根?
(2)正数的平方根有几个?它们之间的关系是什么?负数有没有平方根?0的平方根是什么?
正数的平方根有两个,它们之间互为相反数,负数没有平方根,0的平方根是0.
x2=a,x=
知识回顾
(3)平方和开平方运算有何关系?
(4)算术平方根和平方根有何区别与联系?
互逆的过程
一个正数的算术平方根只有一个,而平方根有两个,互为相反数;0的算术平方根和平方根都是0;负数没有算术平方根也没有平方根;算术平方根是平方根中的正值部分.
要做一只容积为216 cm3的正方体纸盒,
正方体的棱长是多少?
这个实际问题,在数学上可以转化成一个怎样的计算问题?从中可以抽象出一个什么数学概念?
类比“平方根”定义,给出你的推测.
情景导入
定义:如果一个数的立方等于a,那么这个数就叫做a的立方根,也叫做a的三次方根.
表示方法:一个数a的立方根可以表示为:
根指数
被开方数
其中a是被开方数,3是根指数,3不能省略
(开平方的根指数2一般习惯省去).
读作:三次根号 a,
获取新知
如果正方体的体积为5cm3,正方体的边长又该是多少?
解:设正方体的边长为x,则
所以正方体的边长是
求一个数的立方根的运算,叫做开立方.
立方
开立方
互逆
到现在我们学了几种运算
+,-,×,÷,乘方,开方(开平方,开立方)
求立方根的方法:若x3=a ,则 =x;也就是说找出立方等于a的数即为a的平方根。
-27
2
27
0
0.1
通过这些题目的解答,你能看出正数、0、负数的
立方根各有什么特点
怎样求下列括号内的数 各题中已知什么数 求什么数
(1)( )3=0.001; (2)( )3=- ;
(3)( )3=0; (4)33=( );
(5)( )3=8; (6)(-3)3=( ).
(2)利用 可以把求一个负数的立方根
转化为求一个正数的立方根的相反数.
立方根性质:
(1)正数的立方根是正数;
(2)负数的立方根是负数;
(3)0的立方根是0;
(4);
要点精析:
(1) 互为相反数的数的立方根也互为相反数;
规律:对于任何数a都有
2
-2
-3
4
0
计算下面各题,你能发现什么规律?
规律:对于任何数a都有
8
-8
27
-27
0
计算下面各题,你能发现什么规律?
平方根和立方根的异同点
被开方数 平方根 立方根
有两个互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
正数
负数
零
立方根是它本身的数有那些
有1, -1, 0
平方根是它本身的数呢
只有0
例1 求下列各数的立方根.
(1) ;(2)-125;(3)-0.008.
(2) 因为(-5) =-125,
即 =-5.
(3)因为(-0.2)3=-0.008,
所以 .
解:(1) 因为
所以
求一个负数的立方根,可以先求出这个负数绝对值的立方根,然后再取它的相反数.
例题讲解
说明:用计算器求一个有理数的立方根,只需直接按书写顺序按键即可.
例2 用计算器求下列各数的立方根:
(1)1331 ; (2)9.263(精确到0.01).
解:(1)在计算器上依次键入:
显示结果为11,所以
3
3
1
SHIFT
=
1
(2)在计算器上依次键入:
显示结果为 2.1001511606987 ,要求精确到0.01,可得
2.10
9
.
2
6
3
=
SHIFT
1. 64的立方根为( )
A.4 B.±4 C.8 D.±8
A
2.下列说法正确的是( )
A.0.8的立方根是0.2
B.1的立方根为±1
C.-1的立方根是-1
D.-25没有立方根
C
随堂演练
3.求下列各式的值:
(1) ; (2) ; (3) ; (4) .
4.因为(____)3=-27,所以-27的立方根是________,用数学式子表示为__________;因为(______)3=0,所以0的立方根是________,用数学式子表示为________;因为(______)3=8,所以8的立方根是________,用数学式子表示为________.
-3
-3
0
0
2
2
5.已知:x-2的平方根是±2,2x+y+7的立方根是3,
求x2+y2的算术平方根.
解:因为x-2的平方根是±2,
所以x-2=4. 所以x=6.
因为2x+y+7的立方根是3,
所以2x+y+7=27.
把x=6代入解得:y=8,
所以x2+y2=62+82=100.
所以x2+y2的算术平方根为10.
都是开方运算的结果.
平方根与立方根
正数有两个平方根,它们互为相反数;负数没有平方根.
主要区别:
正数有一个立方根,仍为正数;负数有一个立方根,仍为负数.
联系:
非负数都有平方根和立方根;0的平方根和立方根都是0.
课堂小结
(1)
(2)
(1)
(2)
