华师大版数学八年级上册同步课件:11.2 第2课时 实数的大小比较及运算(共13张PPT)
文档属性
| 名称 | 华师大版数学八年级上册同步课件:11.2 第2课时 实数的大小比较及运算(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 217.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 20:27:55 | ||
图片预览





文档简介
(共13张PPT)
11.2 第2课时 实数的大小比较及运算
将两个边长为1的正方形剪拼成一个大正方形.
你能得到长度为 的线段吗?
1
1
a
a=?
探究:
情景导入
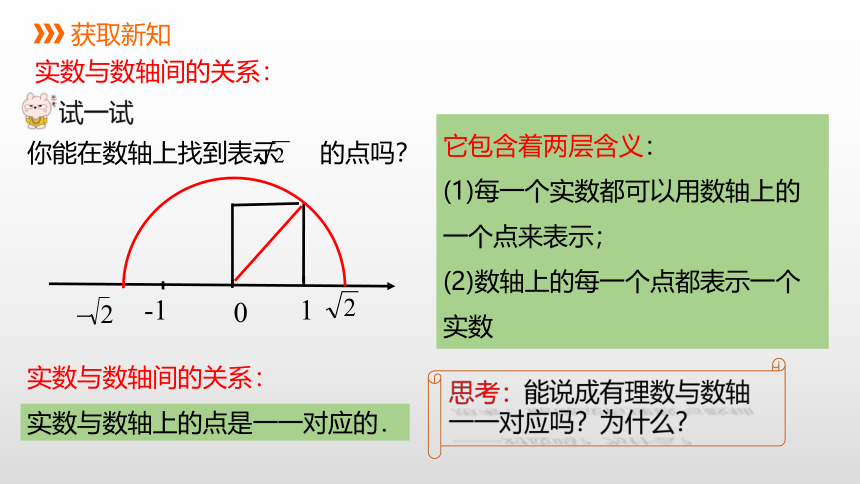
你能在数轴上找到表示 的点吗?
0
1
-1
它包含着两层含义:
(1)每一个实数都可以用数轴上的一个点来表示;
(2)数轴上的每一个点都表示一个实数
实数与数轴间的关系:
实数与数轴上的点是一一对应的.
思考:能说成有理数与数轴一一对应吗?为什么?
获取新知
实数与数轴间的关系:
怎样比较3和 的大小呢?
思考
有理数大小比较法则在实数范围内依然适用;
2.利用数轴比较实数的大小:在数轴上,右边的点对应的数总比左边的大。
1.正实数大于0,负实数小于0;正实数大于一切负实数;两个负数比较大小,绝对值大的反而小
正数大于负数,所以3大于 。
在实数范围内,进行加、减、乘、除、乘方和开方运算时,有理数的运算法则和运算律仍然适用;实数混合运算的运算顺序与有理数的混合运算顺序一样,先算乘方、开方,再算乘除,最后算加减,同级运算按照自左向右的顺序进行,有括号先算括号里面的.
实数的运算:
例1 点A在数轴上表示的数为 ,点B在数轴上表示的数为-5,则A,B两点之间的距离为________.
解:
例题讲解
根据数轴上两点间的距离等于右边的点表示的数减去左边的点表示的数,列式计算即可得解.
数轴上两点间距离的求法:数轴上两点间的距离等于这两点表示的数之差的绝对值.
:实数的大小比较,通常可取它们的近似值在数轴表示来进行.
例2 把下列实数表示在数轴上,并比较它们的大小.(用“<”号连接)
解:在数轴上表示的两个实数,右边的数总比左边的数大.
<
<
<
<
-2
-1
0
2
1
1.5
例3 计算: (精确到0.01)
解:
于是
:取近似值计算时,中间结果通常应比要求的精度多取一位。
1.如图,数轴上的A,B,C,D四点中,与表示数 - 的点最接近的是( )
A.点A B.点B C.点C D.点D
B
随堂演练
2.判断
1.两个无理数之积不一定是无理数.( )
2.两个无理数之和一定是无理数.( )
3.数轴上的任何一点都可以表示实数.( )
×
4.如图,在数轴上点A和点B之间的整数是 .
A
B
3.在 -3, -3.14 , 这四个实数中,最小的是( )
A. -3 B. C. -3.14 D.
D
2
-π
-π
5.计算 :
(-1)2020-2×(1- ) ( ≈1.73,精确到0.1).
解:原式=1-2+2×
≈-1+2×1.73
=-1+3.46
≈2.5
实数
①实数与数轴上点的对应关系:
实数与数轴上点的一一对应
②实数的大小比较:利用比较法则和数轴法。
③实数的运算:实数运算的法则和运算律和有理数相同。运算时要先确定运算符号及顺序,再进行运算,运算过程中要熟练运用运算律及各种运算法则。
课堂小结
11.2 第2课时 实数的大小比较及运算
将两个边长为1的正方形剪拼成一个大正方形.
你能得到长度为 的线段吗?
1
1
a
a=?
探究:
情景导入
你能在数轴上找到表示 的点吗?
0
1
-1
它包含着两层含义:
(1)每一个实数都可以用数轴上的一个点来表示;
(2)数轴上的每一个点都表示一个实数
实数与数轴间的关系:
实数与数轴上的点是一一对应的.
思考:能说成有理数与数轴一一对应吗?为什么?
获取新知
实数与数轴间的关系:
怎样比较3和 的大小呢?
思考
有理数大小比较法则在实数范围内依然适用;
2.利用数轴比较实数的大小:在数轴上,右边的点对应的数总比左边的大。
1.正实数大于0,负实数小于0;正实数大于一切负实数;两个负数比较大小,绝对值大的反而小
正数大于负数,所以3大于 。
在实数范围内,进行加、减、乘、除、乘方和开方运算时,有理数的运算法则和运算律仍然适用;实数混合运算的运算顺序与有理数的混合运算顺序一样,先算乘方、开方,再算乘除,最后算加减,同级运算按照自左向右的顺序进行,有括号先算括号里面的.
实数的运算:
例1 点A在数轴上表示的数为 ,点B在数轴上表示的数为-5,则A,B两点之间的距离为________.
解:
例题讲解
根据数轴上两点间的距离等于右边的点表示的数减去左边的点表示的数,列式计算即可得解.
数轴上两点间距离的求法:数轴上两点间的距离等于这两点表示的数之差的绝对值.
:实数的大小比较,通常可取它们的近似值在数轴表示来进行.
例2 把下列实数表示在数轴上,并比较它们的大小.(用“<”号连接)
解:在数轴上表示的两个实数,右边的数总比左边的数大.
<
<
<
<
-2
-1
0
2
1
1.5
例3 计算: (精确到0.01)
解:
于是
:取近似值计算时,中间结果通常应比要求的精度多取一位。
1.如图,数轴上的A,B,C,D四点中,与表示数 - 的点最接近的是( )
A.点A B.点B C.点C D.点D
B
随堂演练
2.判断
1.两个无理数之积不一定是无理数.( )
2.两个无理数之和一定是无理数.( )
3.数轴上的任何一点都可以表示实数.( )
×
4.如图,在数轴上点A和点B之间的整数是 .
A
B
3.在 -3, -3.14 , 这四个实数中,最小的是( )
A. -3 B. C. -3.14 D.
D
2
-π
-π
5.计算 :
(-1)2020-2×(1- ) ( ≈1.73,精确到0.1).
解:原式=1-2+2×
≈-1+2×1.73
=-1+3.46
≈2.5
实数
①实数与数轴上点的对应关系:
实数与数轴上点的一一对应
②实数的大小比较:利用比较法则和数轴法。
③实数的运算:实数运算的法则和运算律和有理数相同。运算时要先确定运算符号及顺序,再进行运算,运算过程中要熟练运用运算律及各种运算法则。
课堂小结
