华师大版数学八年级上册同步课件:12.1 第3课时 积的乘方(共16张PPT)
文档属性
| 名称 | 华师大版数学八年级上册同步课件:12.1 第3课时 积的乘方(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 319.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 14:33:00 | ||
图片预览





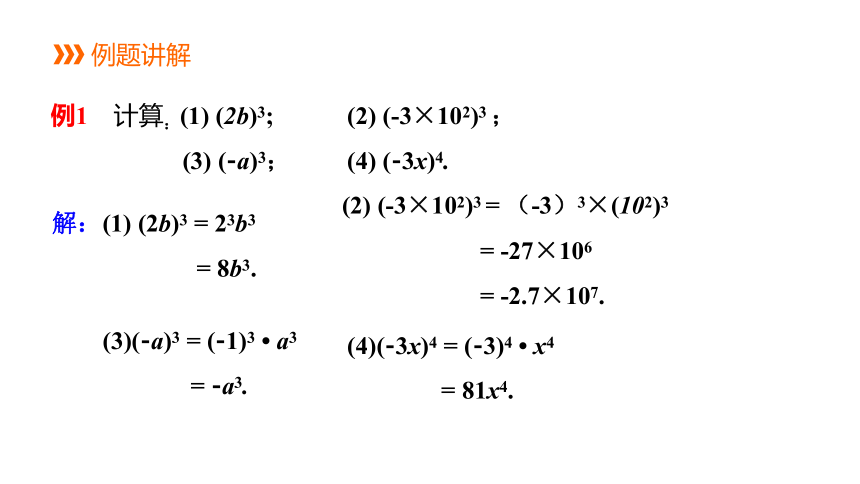
文档简介
(共16张PPT)
12.1 第3课时 积的乘方
第12章 整式的乘除
1.计算:
(1) 10×102× 103 =____ ;(2) (x5 )2=____.
x10
106
2.(1)同底数幂的乘法 :am·an= ( m,n都是正整数).
am+n
(2)幂的乘方:(am)n= (m,n都是正整数).
amn
知识回顾
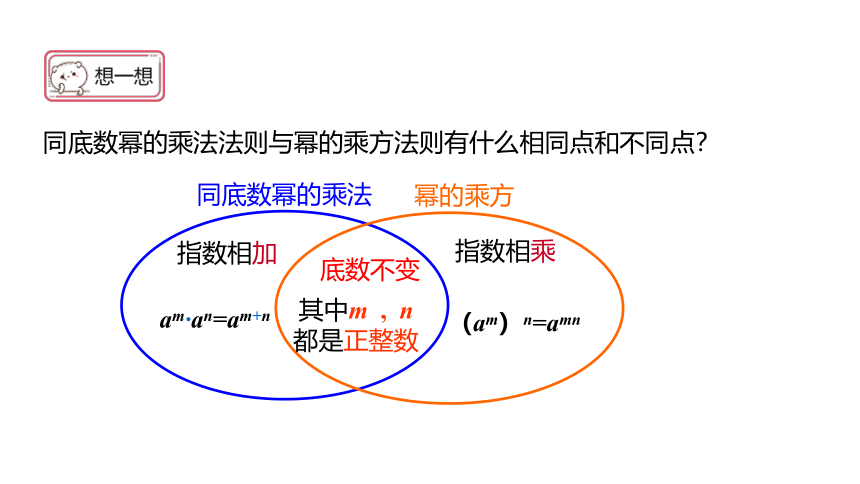
同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
底数不变
指数相乘
指数相加
同底数幂的乘法
幂的乘方
其中m , n都是正整数
(am)n=amn
am·an=am+n
(1)(ab)2 = (ab) (ab)=(aa) (bb)
=a( )b ( );
(2)(ab)3 =______________=___________
=a( )b( ) ;
(3)(ab)4=___________________=_____________
=a( )b( ) ;
2
2
3
3
(ab) (ab) (ab)
(aaa) (bbb)
(ab) (ab) (ab) (ab)
(aaaa) (bbbb)
4
4
这几道题的计算结果有什么规律?设n为正整数,(ab)n等于什么?
你能根据乘方的意义和乘法运算律填空吗?
获取新知
文字语言:积的乘方,把积的每一个因式分别乘方,
再把所得的幂相乘.
符号语言:(ab)n=anbn(n为正整数).
积的乘方法则
:三个或三个以上的积的乘方等于什么?
(abc)n = anbncn (n为正整数)
例1 计算:(1) (2b)3; (2) (-3×102)3 ;
(3) (-a)3; (4) (-3x)4.
解:(1) (2b)3 = 23b3
= 8b3.
(2) (-3×102)3 = (-3)3×(102)3
= -27×106
= -2.7×107.
(3)(-a)3 = (-1)3 a3
= -a3.
(4)(-3x)4 = (-3)4 x4
= 81x4.
例题讲解
利用积的乘方法则计 算时,要先确定积中的因式,然后将每个 因式都乘方,最后求出所有幂的积.
系数乘方时,要带前面符号,特别是系数为-1时,不要漏掉.
科学记数法形式的 数乘方最后的结果应该用科学记数法形式表示.
例2 用简便方法计算:
(1) ×0.254× ×(-4)4;
(2)0.1252 015×(-82 016).
解:(1) ×0.254× ×(-4)4
= ×[0.254×(-4)4]
= ×(0.25×4)4=1×1=1.
(2)0.1252 015×(-82 016)
=-0.1252 015×82 016
=-0.1252 015×82 015×8
=-(0.125×8)2 015×8
=-12 015×8=-8.
逆用积的乘方的情况:
1.两个底数互为倒数;
2.两个底数的积为整数
an·bn = (ab)n
作用:使运算更加简便快捷!
1.计算(a2b)3的结果是( )
A.a6b3 B.a2b3
C.a5b3 D.a6b
2.计算(-xy3)2的结果是( )
A.x2y6 B.-x2y6
C.x2y9 D.-x2y9
A
A
随堂演练
3.计算:
(1) (2m)3 ; (2) (-xy)5; (3) (5ab2)3 ;
(4) 2(x3)2·x3-(3x3)3+(5x)2·x7;
解:(1)原式= 23 ·m3
=8m3;
(2)原式=(-x)5 ·y5
=-x5y5;
(3)原式=53 ·a3 ·(b2)3
=125 a3 b6;
(4)原式=2x6·x3-27x9+25x2·x7
= 2x9-27x9+25x9
= 0;
4.如果5n=a,4n=b,那么20n=____.
ab
5. (1)计算:0.12515×(215)3;
(2)若am=3,bm= ,求(ab)2m的值.
解:(1)原式= ×(23)15= =1.
(2)因为am=3,bm= ,
所以(ab)2m=[(ab)m]2=(ambm)2=
(1)逆用积的乘方法则,可使乘积出现一些简单的数值,从而使解题简单;
(2)直接求字母a,b的值很困难,本题可以运用幂的运算性质变形,然后整体代入求解.
幂的运算性质
性质
am·an=am+n (am)n=amn
(ab)n=anbn ( m,n都是正整数)
反向运用
am · an =am+n、
(am)n =amn
an·bn = (ab)n
可使某些计算简捷
注意
运用积的乘方法则时要注意:公式中的a,b代表任何代数式;每一个因式都要“乘方”;注意结果的符号、幂指数及其逆向运用(混合运算要注意运算顺序)
课堂小结
12.1 第3课时 积的乘方
第12章 整式的乘除
1.计算:
(1) 10×102× 103 =____ ;(2) (x5 )2=____.
x10
106
2.(1)同底数幂的乘法 :am·an= ( m,n都是正整数).
am+n
(2)幂的乘方:(am)n= (m,n都是正整数).
amn
知识回顾
同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
底数不变
指数相乘
指数相加
同底数幂的乘法
幂的乘方
其中m , n都是正整数
(am)n=amn
am·an=am+n
(1)(ab)2 = (ab) (ab)=(aa) (bb)
=a( )b ( );
(2)(ab)3 =______________=___________
=a( )b( ) ;
(3)(ab)4=___________________=_____________
=a( )b( ) ;
2
2
3
3
(ab) (ab) (ab)
(aaa) (bbb)
(ab) (ab) (ab) (ab)
(aaaa) (bbbb)
4
4
这几道题的计算结果有什么规律?设n为正整数,(ab)n等于什么?
你能根据乘方的意义和乘法运算律填空吗?
获取新知
文字语言:积的乘方,把积的每一个因式分别乘方,
再把所得的幂相乘.
符号语言:(ab)n=anbn(n为正整数).
积的乘方法则
:三个或三个以上的积的乘方等于什么?
(abc)n = anbncn (n为正整数)
例1 计算:(1) (2b)3; (2) (-3×102)3 ;
(3) (-a)3; (4) (-3x)4.
解:(1) (2b)3 = 23b3
= 8b3.
(2) (-3×102)3 = (-3)3×(102)3
= -27×106
= -2.7×107.
(3)(-a)3 = (-1)3 a3
= -a3.
(4)(-3x)4 = (-3)4 x4
= 81x4.
例题讲解
利用积的乘方法则计 算时,要先确定积中的因式,然后将每个 因式都乘方,最后求出所有幂的积.
系数乘方时,要带前面符号,特别是系数为-1时,不要漏掉.
科学记数法形式的 数乘方最后的结果应该用科学记数法形式表示.
例2 用简便方法计算:
(1) ×0.254× ×(-4)4;
(2)0.1252 015×(-82 016).
解:(1) ×0.254× ×(-4)4
= ×[0.254×(-4)4]
= ×(0.25×4)4=1×1=1.
(2)0.1252 015×(-82 016)
=-0.1252 015×82 016
=-0.1252 015×82 015×8
=-(0.125×8)2 015×8
=-12 015×8=-8.
逆用积的乘方的情况:
1.两个底数互为倒数;
2.两个底数的积为整数
an·bn = (ab)n
作用:使运算更加简便快捷!
1.计算(a2b)3的结果是( )
A.a6b3 B.a2b3
C.a5b3 D.a6b
2.计算(-xy3)2的结果是( )
A.x2y6 B.-x2y6
C.x2y9 D.-x2y9
A
A
随堂演练
3.计算:
(1) (2m)3 ; (2) (-xy)5; (3) (5ab2)3 ;
(4) 2(x3)2·x3-(3x3)3+(5x)2·x7;
解:(1)原式= 23 ·m3
=8m3;
(2)原式=(-x)5 ·y5
=-x5y5;
(3)原式=53 ·a3 ·(b2)3
=125 a3 b6;
(4)原式=2x6·x3-27x9+25x2·x7
= 2x9-27x9+25x9
= 0;
4.如果5n=a,4n=b,那么20n=____.
ab
5. (1)计算:0.12515×(215)3;
(2)若am=3,bm= ,求(ab)2m的值.
解:(1)原式= ×(23)15= =1.
(2)因为am=3,bm= ,
所以(ab)2m=[(ab)m]2=(ambm)2=
(1)逆用积的乘方法则,可使乘积出现一些简单的数值,从而使解题简单;
(2)直接求字母a,b的值很困难,本题可以运用幂的运算性质变形,然后整体代入求解.
幂的运算性质
性质
am·an=am+n (am)n=amn
(ab)n=anbn ( m,n都是正整数)
反向运用
am · an =am+n、
(am)n =amn
an·bn = (ab)n
可使某些计算简捷
注意
运用积的乘方法则时要注意:公式中的a,b代表任何代数式;每一个因式都要“乘方”;注意结果的符号、幂指数及其逆向运用(混合运算要注意运算顺序)
课堂小结
