华师大版 八年级数学上册 12.2 多项式与多项式相乘 同步课件(共16张PPT)
文档属性
| 名称 | 华师大版 八年级数学上册 12.2 多项式与多项式相乘 同步课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 283.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 19:58:51 | ||
图片预览






文档简介
(共16张PPT)
12.2 第3课时 多项式与多项式相乘
第12章 整式的乘除
知识回顾
1.如何进行单项式与多项式乘法的运算?
② 再把所得的积相加.
① 将单项式分别乘以多项式的各项;
2.进行单项式与多项式乘法运算时,要注意什么
① 不能漏乘:即单项式要乘遍多项式的每一项;
② 去括号时:注意符号的确定.
获取新知
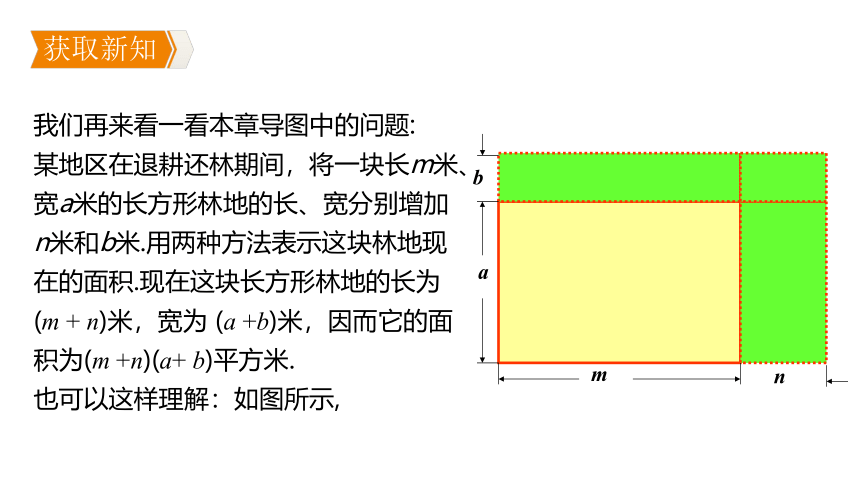
我们再来看一看本章导图中的问题:
某地区在退耕还林期间,将一块长m米、宽a米的长方形林地的长、宽分别增加n米和b米.用两种方法表示这块林地现在的面积.现在这块长方形林地的长为(m + n)米,宽为 (a +b)米,因而它的面积为(m +n)(a+ b)平方米.
也可以这样理解:如图所示,
a
m
b
n
ma
na
mb
nb
a
m
b
n
这块林地由四小块组成,它们的面积分别为ma平方米、mb平方米、na 平方米和nd平方米,故这块林地的面积为(ma+mb+ma+nb)平方米.
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=
ma
+ mb
+ na
+ nb.
如何进行多项式与多项式相乘的运算?
实际上,把(m+n)看成一个整体,有:
= ma+mb+na+nb.
(m+n)(a+b)
= (m+n)a+(m+n)b
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
多项式乘以多项式
1
2
3
4
(m+n)(a+b)
=
ma
1
2
3
4
+na
+mb
+nb
(1)该多项式乘多项式法则的实质是将多项式与多项式相乘转化为几个单项式相乘 的和的形式 .
(2)计算结果中一定要注意合 并同类项 .
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
例题讲解
例1 计算: (1)(x +2)(x-3);(2)(2x + 5y) (3x-2y).
解:(1) (x+2) (x-3)
=x2-3x+2x- 6
=x2-x-6.
(2) (2ac+5y) (3x-2y)
=6x-4xy+15yx-10y
=6x+11xy-10y .
例2 计算:(1)(m - 2n) (m2 + mn-3n2); (2)(3x2-2x+2)(2x+1).
解:(1) (m-2n) (m2 + mn-3n2)
=m m2+m mn-m 3n2-2n m2-2n mn+2n 3n2
=m3+m2n-3mn2-2m2n-2mn2+6n3
=m3-m2n-5mn2+6n3 .
(2)(3x2-2x+2)(2x+1)
= 6x3+3x2-4x2 -2x+4x+2
= 6x3-x2 +2x+2.
注意:别漏乘;
看符号;要化简
多项式与多项式相乘,为了做到不重不漏,可以用“箭头法”标注求解.
如计算 时,可在草稿纸上作如下标注:
,根据箭头指示,结合对象,即可得到
-3x·2x,-3x· ,把各项相加,继续求解即可.
随堂演练
1. 计算(x-1)(2x+3)的结果是( )
A.2x2+x-3 B.2x2-x-3
C.2x2-x+3 D.x2-2x-3
A
2.计算: (1)(3x+1)(x+2); (2)(x-8)(x-y);
(3) (x+y)(x2-xy+y2).
解: (1) 原式=3x·x+2×3x+1·x+1×2
=3x2+6x+x+2
=3x2+7x+2;
(2) 原式=x·x-xy-8x+8y
=x2-xy-8x+8y;
(3) 原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
= x3+y3.
3. 在图①到图②的拼图过程中,所反映的关系式是( )
A.(x-2)(x-3)=x2-5x+6
B.(x+6)(x-1)=x2+5x-6
C.(x-2)(x-3)=x2-5x+6
D.(x+2)(x+3)=x2+5x+6
D
4.若(x-1)(x+3)=x2+mx+n,那么m,n的值分别是( )
A.m=1,n=3 B.m=2,n=-3
C.m=4,n=5 D.m=-2,n=3
B
5.
观察上面四个等式,你能发现什么规律?并应用这个规律解决下面的问题.
5 6
(-3) (-4)
2 (-8)
(-5) 6
口答:
课堂小结
多项式×多项式
运算法则
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加
(a+b)(m+n)=am+an+bm+bn
注意
不要漏乘;正确确定各项符号;结果要最简
实质上是转化为单项式×多项式的运算
12.2 第3课时 多项式与多项式相乘
第12章 整式的乘除
知识回顾
1.如何进行单项式与多项式乘法的运算?
② 再把所得的积相加.
① 将单项式分别乘以多项式的各项;
2.进行单项式与多项式乘法运算时,要注意什么
① 不能漏乘:即单项式要乘遍多项式的每一项;
② 去括号时:注意符号的确定.
获取新知
我们再来看一看本章导图中的问题:
某地区在退耕还林期间,将一块长m米、宽a米的长方形林地的长、宽分别增加n米和b米.用两种方法表示这块林地现在的面积.现在这块长方形林地的长为(m + n)米,宽为 (a +b)米,因而它的面积为(m +n)(a+ b)平方米.
也可以这样理解:如图所示,
a
m
b
n
ma
na
mb
nb
a
m
b
n
这块林地由四小块组成,它们的面积分别为ma平方米、mb平方米、na 平方米和nd平方米,故这块林地的面积为(ma+mb+ma+nb)平方米.
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=
ma
+ mb
+ na
+ nb.
如何进行多项式与多项式相乘的运算?
实际上,把(m+n)看成一个整体,有:
= ma+mb+na+nb.
(m+n)(a+b)
= (m+n)a+(m+n)b
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
多项式乘以多项式
1
2
3
4
(m+n)(a+b)
=
ma
1
2
3
4
+na
+mb
+nb
(1)该多项式乘多项式法则的实质是将多项式与多项式相乘转化为几个单项式相乘 的和的形式 .
(2)计算结果中一定要注意合 并同类项 .
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
例题讲解
例1 计算: (1)(x +2)(x-3);(2)(2x + 5y) (3x-2y).
解:(1) (x+2) (x-3)
=x2-3x+2x- 6
=x2-x-6.
(2) (2ac+5y) (3x-2y)
=6x-4xy+15yx-10y
=6x+11xy-10y .
例2 计算:(1)(m - 2n) (m2 + mn-3n2); (2)(3x2-2x+2)(2x+1).
解:(1) (m-2n) (m2 + mn-3n2)
=m m2+m mn-m 3n2-2n m2-2n mn+2n 3n2
=m3+m2n-3mn2-2m2n-2mn2+6n3
=m3-m2n-5mn2+6n3 .
(2)(3x2-2x+2)(2x+1)
= 6x3+3x2-4x2 -2x+4x+2
= 6x3-x2 +2x+2.
注意:别漏乘;
看符号;要化简
多项式与多项式相乘,为了做到不重不漏,可以用“箭头法”标注求解.
如计算 时,可在草稿纸上作如下标注:
,根据箭头指示,结合对象,即可得到
-3x·2x,-3x· ,把各项相加,继续求解即可.
随堂演练
1. 计算(x-1)(2x+3)的结果是( )
A.2x2+x-3 B.2x2-x-3
C.2x2-x+3 D.x2-2x-3
A
2.计算: (1)(3x+1)(x+2); (2)(x-8)(x-y);
(3) (x+y)(x2-xy+y2).
解: (1) 原式=3x·x+2×3x+1·x+1×2
=3x2+6x+x+2
=3x2+7x+2;
(2) 原式=x·x-xy-8x+8y
=x2-xy-8x+8y;
(3) 原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
= x3+y3.
3. 在图①到图②的拼图过程中,所反映的关系式是( )
A.(x-2)(x-3)=x2-5x+6
B.(x+6)(x-1)=x2+5x-6
C.(x-2)(x-3)=x2-5x+6
D.(x+2)(x+3)=x2+5x+6
D
4.若(x-1)(x+3)=x2+mx+n,那么m,n的值分别是( )
A.m=1,n=3 B.m=2,n=-3
C.m=4,n=5 D.m=-2,n=3
B
5.
观察上面四个等式,你能发现什么规律?并应用这个规律解决下面的问题.
5 6
(-3) (-4)
2 (-8)
(-5) 6
口答:
课堂小结
多项式×多项式
运算法则
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加
(a+b)(m+n)=am+an+bm+bn
注意
不要漏乘;正确确定各项符号;结果要最简
实质上是转化为单项式×多项式的运算
