华师大版数学八年级上册同步课件:12.3 第1课时 两数的和乘以两数的差(共17张PPT)
文档属性
| 名称 | 华师大版数学八年级上册同步课件:12.3 第1课时 两数的和乘以两数的差(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 347.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 14:40:56 | ||
图片预览





文档简介
(共17张PPT)
12.3 第1课时 两数的和乘以两数的差
第12章 整式的乘除
情景导入
王捷同学去商店买了单价是9.8元的糖果10.2千克,售货员刚拿起计算器,王捷就说出应付99.96元,结果与售货员计算出的结果相吻合.售货员很惊讶地说:“你真是个神童,怎么算得这么快 ”
同学们,想知道王捷同学是怎样速算的吗 学习了本节课的知识,你就能知道王捷同学速算的奥秘了.我们快来学习新课吧!
1.如何进行多项式与多项式乘法的运算?
② 再把所得的积相加.
① 先用一个多项式的每一项分别乘以另一个多项式的每一项
2.进行多项式与多项式乘法运算时,要注意什么
① 不能漏乘:即单项式要乘遍多项式的每一项;
② 去括号时:注意符号的确定;
③ 结果:注意要化简
知识回顾
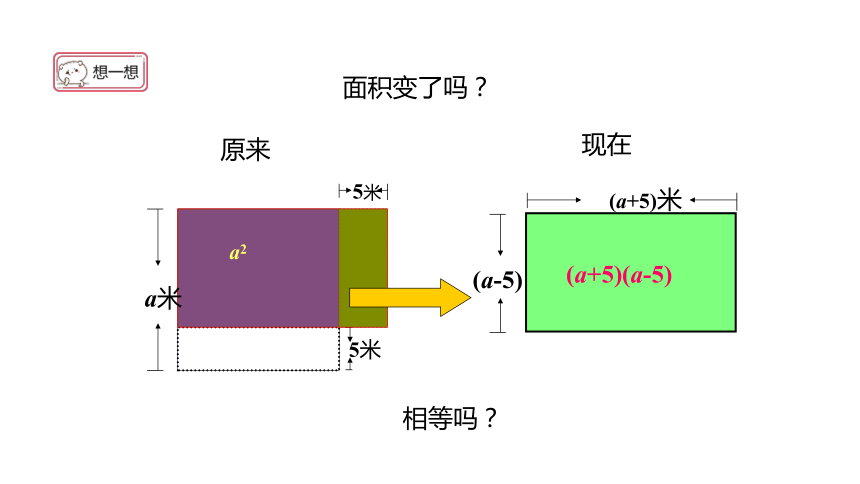
5米
5米
a米
(a-5)
(a+5)米
相等吗?
原来
现在
a2
(a+5)(a-5)
面积变了吗?
①(x + 1)( x-1);
②(m + 2)( m-2);
③(2m+ 1)(2m-1);
④(5y + z)(5y-z).
计算下列多项式的积,你能发现什么规律?
看谁算得又快又准.
x2 - 12
m2-22
(2m)2 - 12
(5y)2 - z2
这些计算结果有什么特点?
完全相同的项的平方减去符号相反的项的平方.
用多项式乘法法则计算:(a+b)(a-b).
(a+b)(a-b)=__________________.
这两个特殊的多项式相乘,得到的结果特别简洁:
这就是说,两数和与这两数差的积,等于这两数的平方差.
这个公式叫做两数和与这两数差的乘法公式,有时也简称
为平方差公式.
(a + b) (a-b)=a2 -b2.
利用这个公式,可以直接计算两数和乘以这两数的差.
a2-ab+ab-b2=a2-b2
获取新知
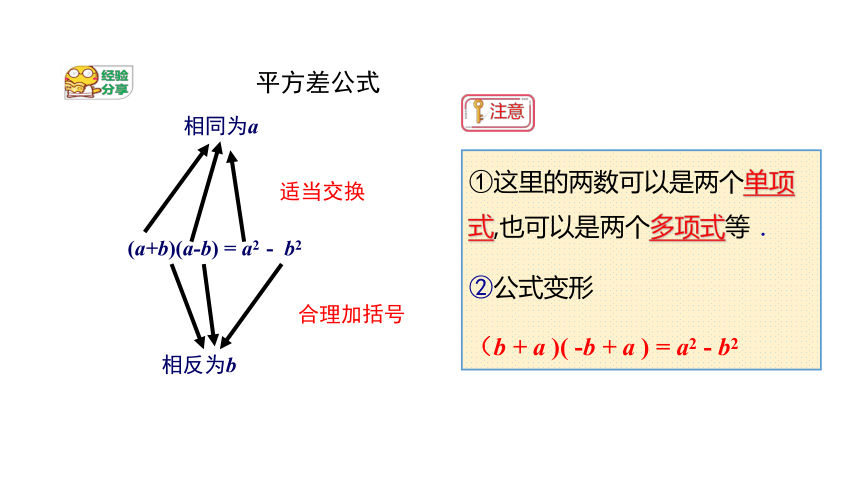
平方差公式
(a+b)(a-b) = a2 - b2
相同为a
相反为b
适当交换
合理加括号
①这里的两数可以是两个单项式,也可以是两个多项式等.
②公式变形
(b + a )( -b + a ) = a2 - b2
几何意义(面积)
a
a
b
b
=
(a-b)(a+b)
(a+b)(a-b)=a2-b2
a2
-b2
下列各式能否用平方差公式进行计算 为什么
(1)(a- b)(a+b); (2)(- b+a)(a- b);
(3)(- a+b)(- a- b); (4)(- a- b)(- b+a).
这两个二项式中有一项完全相同,另一项互为相反数,右边为这两个数的平方差,即完全相同的项的平方减去符号相反的项的平方.(1)(3)(4)能运用平方差公式(2)不能应用公式.
例1 计算: (1)(a+3)(a-3); (2)(2a+3b)(2a-3b);
(3)(1+2c)(1-2c); (4)(-2x-y)(2x-y).
解: (1) (a+3)(a-3)=a2-32=a2-9.
(2)(2a+3b)(2a-3b)=(2a)2-(3b)2=4a2-9b2.
(3) (1+2c)(1-2c)=12-(2c)2=1-4c2.
(4)(-2x-y)(2x-y)=(-y-2x)(-y+2x)=(-y)2-(2x)2=y2-4x2.
例题讲解
例2 计算:1 998 ×2 002.
解:1 998×2 002
=(2 000-2)×(2 000 + 2)
=2 0002-22
=4 000 000 -4
=3 999 996.
1.下列计算能运用平方差公式的是( )
A.(m+n)(-m-n) B.(2x+3)(3x-2)
C.(5a2-b2c)(bc2+5a2) D.
D
随堂演练
2.下列运算正确的是( )
A.(a+b)(b-a)=a2-b2
B.(2m+n)(2m-n)=2m2-n2
C.(xm+3)(xm-3)=x2m-9
D.(x-1)(x+1)=(x-1)2
C
3. 观察算式(2x+y)(2x-y)可以发现这两个二项式中完全相同的项是_____,互为相反数的项是____和_____,利用平方差公式(a+b)(a-b)=________,可知原式=(___)2-(___)2=________.
2x
y
-y
a2-b2
2x
y
4x2-y2
4.利用平方差公式计算:
(1)(a+3b)(a- 3b); (2)(3+2a)(-3+2a);
(3)(-2x2-y)(-2x2+y);(4)(3x+4)(3x-4)-(2x+3)(3x-2).
解:(1)原式=a2-(3b)2
=a2-9b2
(2)原式=(2a+3)(2a-3)
=(2a)2-32
=4a2-9
(3)原式=(-2x2 )2-y2
=4x4-y2
(4)原式=(9x2-16)-(6x2+5x -6)
=3x2-5x- 10.
5.运用平方差公式简便运算
(1)2 014×2 016-2 0152; (2)1.03×0.97;
(3)40 ×39 .
解:(1)原式=(2 015-1)×(2 015+1)-2 0152
=2 0152-1-2 0152=-1;
(2)原式=(1+0.03)×(1-0.03)=12-0.032
=1-0.000 9=0.999 1;
(3)原式=
=1 600- =1 599 .
平方差公式
内容
注意
两个数的和与这两个数的差的积,等于这两个数的平方差
1.符号表示:(a+b)(a-b)=a2-b2
2.紧紧抓住 “一同一反”这一特征,在应用时,只有两个二项式的积才有可能应用平方差公式;不能直接应用公式的,要经过变形才可以应用
课堂小结
12.3 第1课时 两数的和乘以两数的差
第12章 整式的乘除
情景导入
王捷同学去商店买了单价是9.8元的糖果10.2千克,售货员刚拿起计算器,王捷就说出应付99.96元,结果与售货员计算出的结果相吻合.售货员很惊讶地说:“你真是个神童,怎么算得这么快 ”
同学们,想知道王捷同学是怎样速算的吗 学习了本节课的知识,你就能知道王捷同学速算的奥秘了.我们快来学习新课吧!
1.如何进行多项式与多项式乘法的运算?
② 再把所得的积相加.
① 先用一个多项式的每一项分别乘以另一个多项式的每一项
2.进行多项式与多项式乘法运算时,要注意什么
① 不能漏乘:即单项式要乘遍多项式的每一项;
② 去括号时:注意符号的确定;
③ 结果:注意要化简
知识回顾
5米
5米
a米
(a-5)
(a+5)米
相等吗?
原来
现在
a2
(a+5)(a-5)
面积变了吗?
①(x + 1)( x-1);
②(m + 2)( m-2);
③(2m+ 1)(2m-1);
④(5y + z)(5y-z).
计算下列多项式的积,你能发现什么规律?
看谁算得又快又准.
x2 - 12
m2-22
(2m)2 - 12
(5y)2 - z2
这些计算结果有什么特点?
完全相同的项的平方减去符号相反的项的平方.
用多项式乘法法则计算:(a+b)(a-b).
(a+b)(a-b)=__________________.
这两个特殊的多项式相乘,得到的结果特别简洁:
这就是说,两数和与这两数差的积,等于这两数的平方差.
这个公式叫做两数和与这两数差的乘法公式,有时也简称
为平方差公式.
(a + b) (a-b)=a2 -b2.
利用这个公式,可以直接计算两数和乘以这两数的差.
a2-ab+ab-b2=a2-b2
获取新知
平方差公式
(a+b)(a-b) = a2 - b2
相同为a
相反为b
适当交换
合理加括号
①这里的两数可以是两个单项式,也可以是两个多项式等.
②公式变形
(b + a )( -b + a ) = a2 - b2
几何意义(面积)
a
a
b
b
=
(a-b)(a+b)
(a+b)(a-b)=a2-b2
a2
-b2
下列各式能否用平方差公式进行计算 为什么
(1)(a- b)(a+b); (2)(- b+a)(a- b);
(3)(- a+b)(- a- b); (4)(- a- b)(- b+a).
这两个二项式中有一项完全相同,另一项互为相反数,右边为这两个数的平方差,即完全相同的项的平方减去符号相反的项的平方.(1)(3)(4)能运用平方差公式(2)不能应用公式.
例1 计算: (1)(a+3)(a-3); (2)(2a+3b)(2a-3b);
(3)(1+2c)(1-2c); (4)(-2x-y)(2x-y).
解: (1) (a+3)(a-3)=a2-32=a2-9.
(2)(2a+3b)(2a-3b)=(2a)2-(3b)2=4a2-9b2.
(3) (1+2c)(1-2c)=12-(2c)2=1-4c2.
(4)(-2x-y)(2x-y)=(-y-2x)(-y+2x)=(-y)2-(2x)2=y2-4x2.
例题讲解
例2 计算:1 998 ×2 002.
解:1 998×2 002
=(2 000-2)×(2 000 + 2)
=2 0002-22
=4 000 000 -4
=3 999 996.
1.下列计算能运用平方差公式的是( )
A.(m+n)(-m-n) B.(2x+3)(3x-2)
C.(5a2-b2c)(bc2+5a2) D.
D
随堂演练
2.下列运算正确的是( )
A.(a+b)(b-a)=a2-b2
B.(2m+n)(2m-n)=2m2-n2
C.(xm+3)(xm-3)=x2m-9
D.(x-1)(x+1)=(x-1)2
C
3. 观察算式(2x+y)(2x-y)可以发现这两个二项式中完全相同的项是_____,互为相反数的项是____和_____,利用平方差公式(a+b)(a-b)=________,可知原式=(___)2-(___)2=________.
2x
y
-y
a2-b2
2x
y
4x2-y2
4.利用平方差公式计算:
(1)(a+3b)(a- 3b); (2)(3+2a)(-3+2a);
(3)(-2x2-y)(-2x2+y);(4)(3x+4)(3x-4)-(2x+3)(3x-2).
解:(1)原式=a2-(3b)2
=a2-9b2
(2)原式=(2a+3)(2a-3)
=(2a)2-32
=4a2-9
(3)原式=(-2x2 )2-y2
=4x4-y2
(4)原式=(9x2-16)-(6x2+5x -6)
=3x2-5x- 10.
5.运用平方差公式简便运算
(1)2 014×2 016-2 0152; (2)1.03×0.97;
(3)40 ×39 .
解:(1)原式=(2 015-1)×(2 015+1)-2 0152
=2 0152-1-2 0152=-1;
(2)原式=(1+0.03)×(1-0.03)=12-0.032
=1-0.000 9=0.999 1;
(3)原式=
=1 600- =1 599 .
平方差公式
内容
注意
两个数的和与这两个数的差的积,等于这两个数的平方差
1.符号表示:(a+b)(a-b)=a2-b2
2.紧紧抓住 “一同一反”这一特征,在应用时,只有两个二项式的积才有可能应用平方差公式;不能直接应用公式的,要经过变形才可以应用
课堂小结
