华师大版数学八年级上册同步课件:12.3 两数和(差)的平方(第2课时) (共18张PPT)
文档属性
| 名称 | 华师大版数学八年级上册同步课件:12.3 两数和(差)的平方(第2课时) (共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 373.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
12.3 第2课时 两数和(差)的平方
第12章 整式的乘除
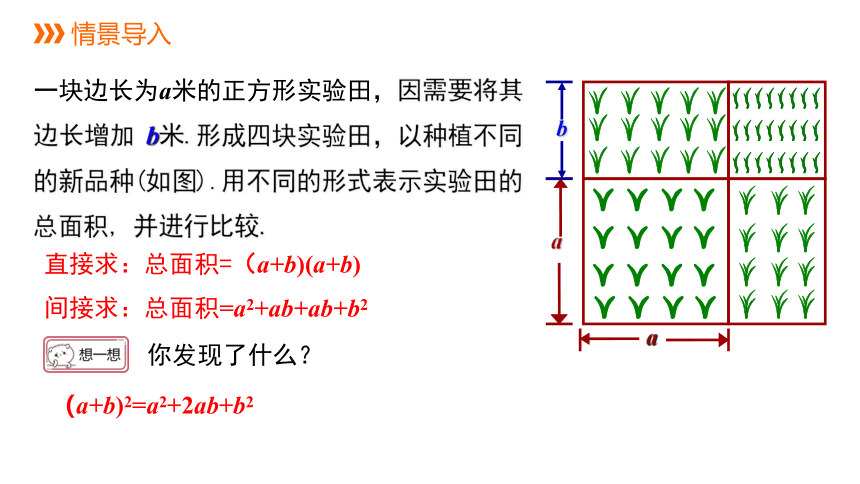
一块边长为a米的正方形实验田,因需要将其边长增加 b米.形成四块实验田,以种植不同的新品种(如图).用不同的形式表示实验田的总面积, 并进行比较.
a
a
b
直接求:总面积=(a+b)(a+b)
间接求:总面积=a2+ab+ab+b2
你发现了什么?
(a+b)2=a2+2ab+b2
情景导入
计算下列多项式的积,你能发现什么规律?
(1) (p+1)2=(p+1)(p+1)= .
p2+2p+1
(2) (m+2)2=(m+2)(m+2)= .
m2+4m+4
(3) (p-1)2=(p-1)(p-1)= .
p2-2p+1
(4) (m-2)2=(m-2)(m-2)= .
m2-4m+4
根据上面的规律,你能直接下面式子的写出答案吗?
(a+b)2= .
a2+2ab+b2
用多项式乘法法则计算:(a+b)2.
(a+b)2=(a+b)(a+b)=___________.
我们又得到一个漂亮的结果:
这就是说,
(a + b)2 =a2 +2ab+b2.
a2+2ab+b2
利用这个公式,可以直接计算两数和的平方.
获取新知
两数和的平方,等于这两数的平方和加上它们的积的2倍.这个公式叫做两数和的平方公式.
完全平方公式
(a+b)2= .
a2+2ab+b2
公式简记为:首平方,尾平方,积的2倍放中央.
4.公式中的字母a,b可以表示数、单项式和多项式.
1.积为二次三项式;
2.积中两项为两数的平方和;
3.另一项是两数积的2倍;
几何意义(面积)
a
2
b
2
ab
ab
a
b
a+b
a+b
a
b
a
2
ab
ab
b
2
(a+b)
2
=
a
2
+
2ab
+
b
2
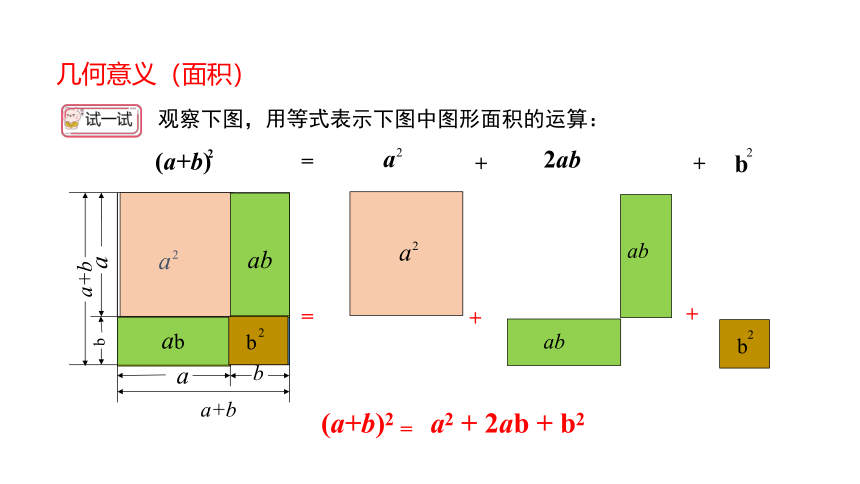
(a+b)2
a2 + 2ab + b2
=
观察下图,用等式表示下图中图形面积的运算:
=
+
+
你能推导两数差的平方公式(a-b)2吗?
注意到a-b=a+(-b),也可以利用两数和的平方公式来计算
这样就得到了两数差的平方公式:
(a-b)2= .
a2-2ab+b2
两数差的平方,等于这两数的平方和减去它们的积的2倍.
几何意义(面积)
=
-
+
(a-b)2
=
a2
b2
-
+
2ab
a
a
b
b
b
b
a-b
a-b
a
a
b
b
观察下图,用等式表示下图中图形面积的运算:
例1 计算:(1)(2x+3y)2;(2)(2a+ )2.
解:(1)(2x+3y)2=(2x)2 +2 2x 3y + (3y)2
=4x2+12xy+9y2.
(2)(2a+ )2=(2a)2 + 2 2a +
=4a2 + 2ab +
例题讲解
例2 计算:(1) (3x-2y)2;(2)
解:(1)(3x-2y)2=(3x)2 - 2 3x 2y + (2y)2
=9x2 -12xy+ 4y2.
(2)解法1
解法2
(2)解法1
解法2
1.运用乘法公式计算(x+3)2的结果是( )
A.x2+9 B.x2-6x+9
C.x2+6x+9 D.x2+3x+9
C
随堂演练
2.运用完全平方公式计算:
(1) (6a+5b)2; (2) (4x-3y)2 ;
(3) (2m-1)2 ; (4)(-2m-1)2 .
解:(1)原式=36a2+60ab+25b2;
(2)原式=16x2-24xy+9y2;
(3)原式=4m2-4m+1;
(4)原式=4m2+4m+1.
3.运用完全平方公式简便计算:
(1) 1022; (2) 992.
解: (1)1022=(100+2)2
=10000+400+4
=10404.
(2)992= (100 –1)2
=10000 -200+1
=9801.
4. 运用乘法公式计算:
(1) (x+2y-3)(x-2y+3) ; (2) (a+b+c)2
(1)原式=[x+(2y–3)][x-(2y-3)]
= x2-(2y-3)2
= x2-(4y2-12y+9)
= x2-4y2+12y-9.
解:
(2)原式 = [(a+b)+c]2
= (a+b)2+2(a+b)c+c2
= a2+2ab+b2+2ac+2bc+c2
= a2+b2+c2+2ab+2bc+2ac.
第(1)题选用平方差公式进行计算,需要分组.分组方法是“符号相同的为一组,符号相反的为另一组”.第(2)题要把其中两项看成一个整体,再按照完全平方公式进行计算.
5.(1). 若a+b=5,ab=-6, 求a2+b2,a2-ab+b2.
(2). 已知x+y=8,x-y=4,求xy.
解:a2+b2=(a+b)2-2ab=52-2×(-6)=37;
a2-ab+b2=a2+b2-ab=37-(-6)=43.
解:∵x+y=8, ∴(x+y)2=64,即x2+y2+2xy=64①;
∵x-y=4, ∴(x-y)2=16,即x2+y2-2xy=16②;
由①-②,得
4xy=48,
∴xy=12.
解题时常用结论:
a2+b2=(a+b)2-2ab
=(a-b)2+2ab; 4ab=(a+b)2-(a-b)2.
1.形式不同.
注意完全平方公式和平方差公式的不同:
2.结果不同
完全平方公式的结果是三项,
即:(a±b)2=a2±2ab+b2
平方差公式的结果是两项,
即:(a+b) (a-b) =a2-b2
1.要找准对应公式中的a和b
2.掌握常见的变形和必要时添加括号
课堂小结
12.3 第2课时 两数和(差)的平方
第12章 整式的乘除
一块边长为a米的正方形实验田,因需要将其边长增加 b米.形成四块实验田,以种植不同的新品种(如图).用不同的形式表示实验田的总面积, 并进行比较.
a
a
b
直接求:总面积=(a+b)(a+b)
间接求:总面积=a2+ab+ab+b2
你发现了什么?
(a+b)2=a2+2ab+b2
情景导入
计算下列多项式的积,你能发现什么规律?
(1) (p+1)2=(p+1)(p+1)= .
p2+2p+1
(2) (m+2)2=(m+2)(m+2)= .
m2+4m+4
(3) (p-1)2=(p-1)(p-1)= .
p2-2p+1
(4) (m-2)2=(m-2)(m-2)= .
m2-4m+4
根据上面的规律,你能直接下面式子的写出答案吗?
(a+b)2= .
a2+2ab+b2
用多项式乘法法则计算:(a+b)2.
(a+b)2=(a+b)(a+b)=___________.
我们又得到一个漂亮的结果:
这就是说,
(a + b)2 =a2 +2ab+b2.
a2+2ab+b2
利用这个公式,可以直接计算两数和的平方.
获取新知
两数和的平方,等于这两数的平方和加上它们的积的2倍.这个公式叫做两数和的平方公式.
完全平方公式
(a+b)2= .
a2+2ab+b2
公式简记为:首平方,尾平方,积的2倍放中央.
4.公式中的字母a,b可以表示数、单项式和多项式.
1.积为二次三项式;
2.积中两项为两数的平方和;
3.另一项是两数积的2倍;
几何意义(面积)
a
2
b
2
ab
ab
a
b
a+b
a+b
a
b
a
2
ab
ab
b
2
(a+b)
2
=
a
2
+
2ab
+
b
2
(a+b)2
a2 + 2ab + b2
=
观察下图,用等式表示下图中图形面积的运算:
=
+
+
你能推导两数差的平方公式(a-b)2吗?
注意到a-b=a+(-b),也可以利用两数和的平方公式来计算
这样就得到了两数差的平方公式:
(a-b)2= .
a2-2ab+b2
两数差的平方,等于这两数的平方和减去它们的积的2倍.
几何意义(面积)
=
-
+
(a-b)2
=
a2
b2
-
+
2ab
a
a
b
b
b
b
a-b
a-b
a
a
b
b
观察下图,用等式表示下图中图形面积的运算:
例1 计算:(1)(2x+3y)2;(2)(2a+ )2.
解:(1)(2x+3y)2=(2x)2 +2 2x 3y + (3y)2
=4x2+12xy+9y2.
(2)(2a+ )2=(2a)2 + 2 2a +
=4a2 + 2ab +
例题讲解
例2 计算:(1) (3x-2y)2;(2)
解:(1)(3x-2y)2=(3x)2 - 2 3x 2y + (2y)2
=9x2 -12xy+ 4y2.
(2)解法1
解法2
(2)解法1
解法2
1.运用乘法公式计算(x+3)2的结果是( )
A.x2+9 B.x2-6x+9
C.x2+6x+9 D.x2+3x+9
C
随堂演练
2.运用完全平方公式计算:
(1) (6a+5b)2; (2) (4x-3y)2 ;
(3) (2m-1)2 ; (4)(-2m-1)2 .
解:(1)原式=36a2+60ab+25b2;
(2)原式=16x2-24xy+9y2;
(3)原式=4m2-4m+1;
(4)原式=4m2+4m+1.
3.运用完全平方公式简便计算:
(1) 1022; (2) 992.
解: (1)1022=(100+2)2
=10000+400+4
=10404.
(2)992= (100 –1)2
=10000 -200+1
=9801.
4. 运用乘法公式计算:
(1) (x+2y-3)(x-2y+3) ; (2) (a+b+c)2
(1)原式=[x+(2y–3)][x-(2y-3)]
= x2-(2y-3)2
= x2-(4y2-12y+9)
= x2-4y2+12y-9.
解:
(2)原式 = [(a+b)+c]2
= (a+b)2+2(a+b)c+c2
= a2+2ab+b2+2ac+2bc+c2
= a2+b2+c2+2ab+2bc+2ac.
第(1)题选用平方差公式进行计算,需要分组.分组方法是“符号相同的为一组,符号相反的为另一组”.第(2)题要把其中两项看成一个整体,再按照完全平方公式进行计算.
5.(1). 若a+b=5,ab=-6, 求a2+b2,a2-ab+b2.
(2). 已知x+y=8,x-y=4,求xy.
解:a2+b2=(a+b)2-2ab=52-2×(-6)=37;
a2-ab+b2=a2+b2-ab=37-(-6)=43.
解:∵x+y=8, ∴(x+y)2=64,即x2+y2+2xy=64①;
∵x-y=4, ∴(x-y)2=16,即x2+y2-2xy=16②;
由①-②,得
4xy=48,
∴xy=12.
解题时常用结论:
a2+b2=(a+b)2-2ab
=(a-b)2+2ab; 4ab=(a+b)2-(a-b)2.
1.形式不同.
注意完全平方公式和平方差公式的不同:
2.结果不同
完全平方公式的结果是三项,
即:(a±b)2=a2±2ab+b2
平方差公式的结果是两项,
即:(a+b) (a-b) =a2-b2
1.要找准对应公式中的a和b
2.掌握常见的变形和必要时添加括号
课堂小结
