华师大版数学八年级上册同步课件:13.2 第2课时 全等三角形的判定条件(共17张PPT)
文档属性
| 名称 | 华师大版数学八年级上册同步课件:13.2 第2课时 全等三角形的判定条件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 317.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 20:32:09 | ||
图片预览



文档简介
(共17张PPT)
13.2 第2课时 全等三角形的判定条件
第13章 全等三角形
对于全等三角形,从它的边角来看,我们知道:若两个三角形的三条边与三个角都分别对应相等,那么这两个三角形一定可以互相重合,即全等。
情境导入
能否减少一些条件,找到更为简便的判定三角形全等的方法.
元旦联欢会,为活跃气氛,班委会想让班级,每个同学自制一个三角形的小彩旗,可怎样才能使全班的彩旗形状、大小完全相同呢
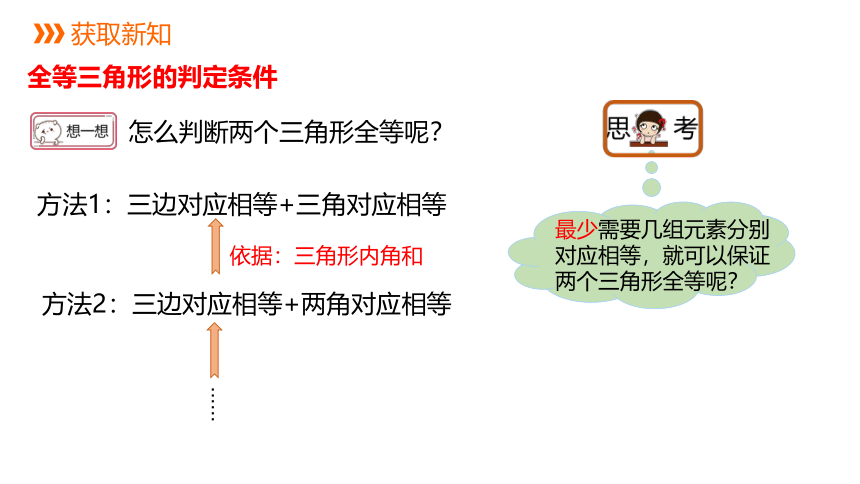
全等三角形的判定条件
怎么判断两个三角形全等呢?
方法1:三边对应相等+三角对应相等
方法2:三边对应相等+两角对应相等
依据:三角形内角和
......
最少需要几组元素分别对应相等,就可以保证两个三角形全等呢?
获取新知
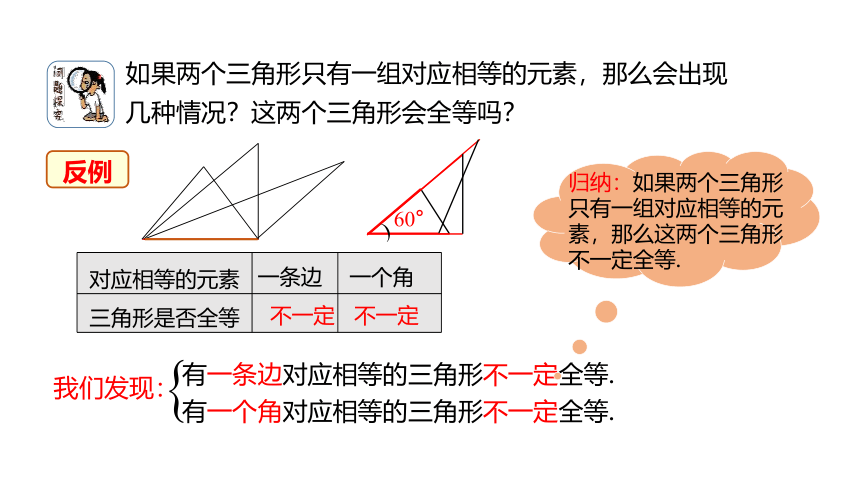
如果两个三角形只有一组对应相等的元素,那么会出现几种情况?这两个三角形会全等吗?
对应相等的元素
三角形是否全等
一条边
一个角
不一定
不一定
反例
有一条边对应相等的三角形不一定全等.
(
60°
有一个角对应相等的三角形不一定全等.
归纳:如果两个三角形只有一组对应相等的元素,那么这两个三角形不一定全等.
我们发现:
由于一个三角形有三条边、三个角共六个元素,所以可能出现的情况会较多.可能的情况有:
两个角对应相等;____________________; __________________.
两个边对应相等
一条边和一个角相等
如果两个三角形有两组对应相等的元素,那么会出现几种可能的情况呢?这时,这两个三角形会全等吗?
在这些情况下,两个三角形会全等吗?
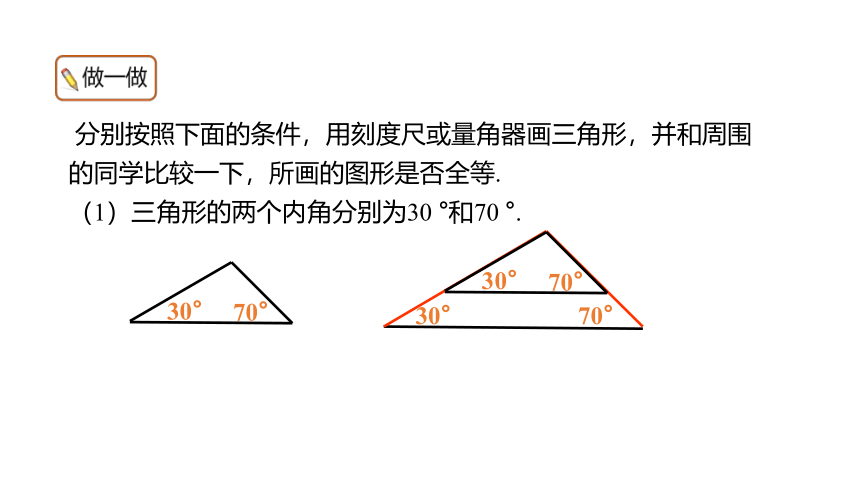
分别按照下面的条件,用刻度尺或量角器画三角形,并和周围的同学比较一下,所画的图形是否全等.
(1)三角形的两个内角分别为30 °和70 °.
30°
70°
30°
70°
30°
70°
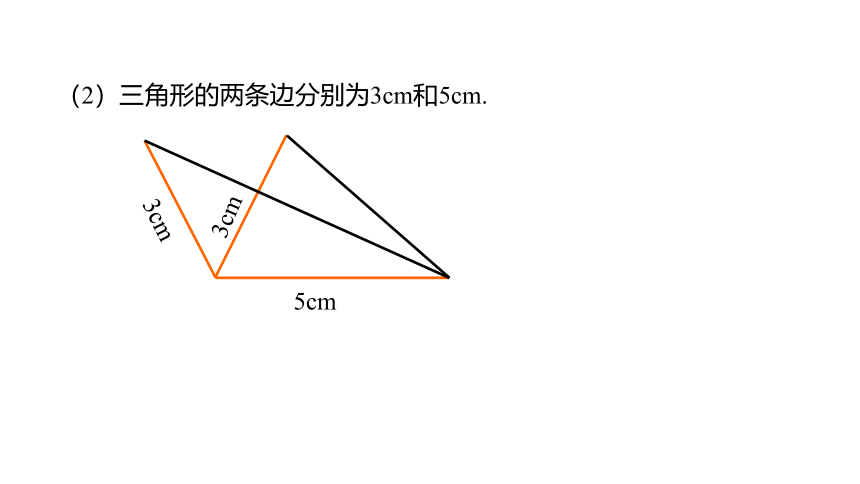
(2)三角形的两条边分别为3cm和5cm.
5cm
3cm
3cm
(3)三角形的一个内角为60°,—条边为3 cm.
(i)这条长3 cm的边是60°角的邻边;
(ii)这条长3 cm的边是60°角的对边.
60°
60°
(
(
3cm
3cm
(i)
60°
(
3cm
60°
(
3cm
(ii)
对应相 等的元素
三角形 是否全等
如果只知道两个三角形有两组对应相等的元素,那么这两个三角形是否全等的情况为:
两角
两边
角+邻边
角+对边
不一定
不一定
不一定
不一定
由以上的探索与发现,我们知道两个三角形只有一组或两组对应相等的元素(边或角),那么这两个三角形不一定全等.
总 结
如果两个三角形有三组对应相等的元素(边或角),又会如何呢?
课后思考一下,下节课我们一起刨根问底。
例1 .如图13-2-7所示,已知△ABC平移后得到△DEF,若∠A=80°,∠E=60°,求∠C的度数.
解:由平移的性质,得△ABC≌△DEF,
∴∠ABC=∠E=60°,
∴∠C=180°-∠A-∠ABC=180°-80°-60°=40°.
例题讲解
总 结
三角形的平移、旋转过程中,形状、大小没有发生改变,即全等变换。
1.下列说法中正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
.
D
随堂演练
2.下列说法正确的是( )
A.三个角对应相等的两个三角形全等
B.判定两个三角形全等的条件中至少有一个是等边
C.面积相等的两个三角形全等
D.周长相等的两个三角形全等
B
3.如图,将△AOB 绕点0 旋转180°,得到△COD,这时△AOB
≌△ .这两个三角形的对应边是:AO与 ,OB与 ,
BA与 ;对应角是: ∠AOB 与 ,
∠OBA 与 , ∠BAO 与_______
COD
CO
OD
DC
∠COD
∠ODC
∠DCO
O
A
B
C
D
4.如图,点D是等腰直角三角形ABC内一点,AB=AC,
将△ABD绕点A逆时针旋转90°,点D与点E重合,则△ABD≌________, AD=_____,BD=____.
△ACE
AE
CE
E
A
B
C
D
5.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则有如下结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC.其中正确结论的个数是( )
A.1个 B.2个
C.3个 D.4个
C
F
A
B
C
E
全等三角形判定的条件
一定全等的情况:3组元素:三边、三角对应相等或三边、两角对应相等。
不一定相等的情况:1组或2组元素:两个三角形只有一 组或两组对应相等的元素(边或角),那么这两个三角形不一定全等.
课堂小结
13.2 第2课时 全等三角形的判定条件
第13章 全等三角形
对于全等三角形,从它的边角来看,我们知道:若两个三角形的三条边与三个角都分别对应相等,那么这两个三角形一定可以互相重合,即全等。
情境导入
能否减少一些条件,找到更为简便的判定三角形全等的方法.
元旦联欢会,为活跃气氛,班委会想让班级,每个同学自制一个三角形的小彩旗,可怎样才能使全班的彩旗形状、大小完全相同呢
全等三角形的判定条件
怎么判断两个三角形全等呢?
方法1:三边对应相等+三角对应相等
方法2:三边对应相等+两角对应相等
依据:三角形内角和
......
最少需要几组元素分别对应相等,就可以保证两个三角形全等呢?
获取新知
如果两个三角形只有一组对应相等的元素,那么会出现几种情况?这两个三角形会全等吗?
对应相等的元素
三角形是否全等
一条边
一个角
不一定
不一定
反例
有一条边对应相等的三角形不一定全等.
(
60°
有一个角对应相等的三角形不一定全等.
归纳:如果两个三角形只有一组对应相等的元素,那么这两个三角形不一定全等.
我们发现:
由于一个三角形有三条边、三个角共六个元素,所以可能出现的情况会较多.可能的情况有:
两个角对应相等;____________________; __________________.
两个边对应相等
一条边和一个角相等
如果两个三角形有两组对应相等的元素,那么会出现几种可能的情况呢?这时,这两个三角形会全等吗?
在这些情况下,两个三角形会全等吗?
分别按照下面的条件,用刻度尺或量角器画三角形,并和周围的同学比较一下,所画的图形是否全等.
(1)三角形的两个内角分别为30 °和70 °.
30°
70°
30°
70°
30°
70°
(2)三角形的两条边分别为3cm和5cm.
5cm
3cm
3cm
(3)三角形的一个内角为60°,—条边为3 cm.
(i)这条长3 cm的边是60°角的邻边;
(ii)这条长3 cm的边是60°角的对边.
60°
60°
(
(
3cm
3cm
(i)
60°
(
3cm
60°
(
3cm
(ii)
对应相 等的元素
三角形 是否全等
如果只知道两个三角形有两组对应相等的元素,那么这两个三角形是否全等的情况为:
两角
两边
角+邻边
角+对边
不一定
不一定
不一定
不一定
由以上的探索与发现,我们知道两个三角形只有一组或两组对应相等的元素(边或角),那么这两个三角形不一定全等.
总 结
如果两个三角形有三组对应相等的元素(边或角),又会如何呢?
课后思考一下,下节课我们一起刨根问底。
例1 .如图13-2-7所示,已知△ABC平移后得到△DEF,若∠A=80°,∠E=60°,求∠C的度数.
解:由平移的性质,得△ABC≌△DEF,
∴∠ABC=∠E=60°,
∴∠C=180°-∠A-∠ABC=180°-80°-60°=40°.
例题讲解
总 结
三角形的平移、旋转过程中,形状、大小没有发生改变,即全等变换。
1.下列说法中正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
.
D
随堂演练
2.下列说法正确的是( )
A.三个角对应相等的两个三角形全等
B.判定两个三角形全等的条件中至少有一个是等边
C.面积相等的两个三角形全等
D.周长相等的两个三角形全等
B
3.如图,将△AOB 绕点0 旋转180°,得到△COD,这时△AOB
≌△ .这两个三角形的对应边是:AO与 ,OB与 ,
BA与 ;对应角是: ∠AOB 与 ,
∠OBA 与 , ∠BAO 与_______
COD
CO
OD
DC
∠COD
∠ODC
∠DCO
O
A
B
C
D
4.如图,点D是等腰直角三角形ABC内一点,AB=AC,
将△ABD绕点A逆时针旋转90°,点D与点E重合,则△ABD≌________, AD=_____,BD=____.
△ACE
AE
CE
E
A
B
C
D
5.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则有如下结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC.其中正确结论的个数是( )
A.1个 B.2个
C.3个 D.4个
C
F
A
B
C
E
全等三角形判定的条件
一定全等的情况:3组元素:三边、三角对应相等或三边、两角对应相等。
不一定相等的情况:1组或2组元素:两个三角形只有一 组或两组对应相等的元素(边或角),那么这两个三角形不一定全等.
课堂小结
