华师大版数学八年级上册同步课件:13.4 第2课时 作垂线和垂直平分线(共20张PPT)
文档属性
| 名称 | 华师大版数学八年级上册同步课件:13.4 第2课时 作垂线和垂直平分线(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 443.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
13.4 第2课时作垂线和垂直平分线
第13章 全等三角形
1.回顾已经学过的基本作图有哪几种?
(1)作一条线段等于已知线段;
(2)作一个角等于已知角;
(3)作已知角的平分线.
2.点与直线的位置关系有几种情况?
(1)点在直线上;(2)点在直线外.
知识回顾
经过一点作已知直线的垂线
获取新知
如何经过一已知点作已知直线的垂线呢?
可分为两种情况来讨论:
经过已知直线上一点作已知直线的垂线.
经过已知直线外一点作已知直线的垂线.
经过一已知点作已知直线的垂线有可以分为几种情况?
经过已知直线上一点作已知直线的垂线
求作的垂线 .
A
B
C
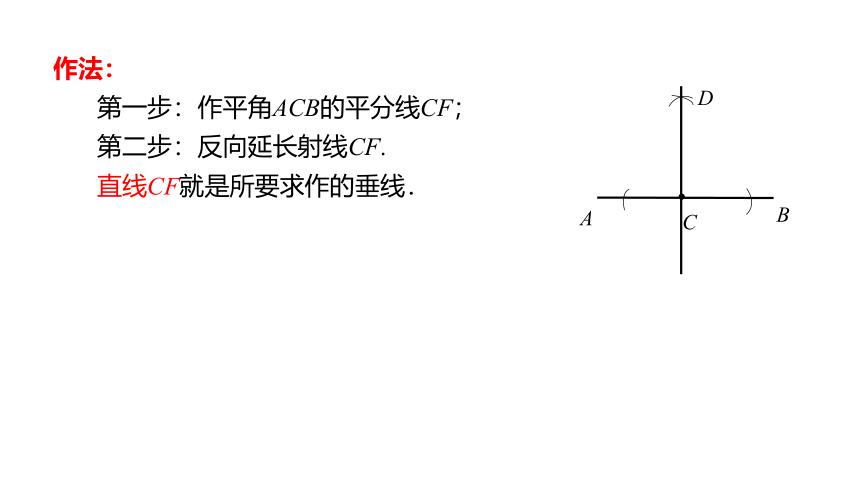
已知直线AB和AB上一点C,用直尺和圆规准确地经过点C作出直线AB的垂线。
分析:如图,由于点C在直线AB上,因此所求作的垂线正好是平角ACB的平分线所在的直线.
平角ACB的平分线所在的直线
转化
作法:
第一步:作平角ACB的平分线CF;
第二步:反向延长射线CF.
直线CF就是所要求作的垂线.
D
C
A
B
经过已知直线外一点作已知直线的垂线
A
B
C
D
E
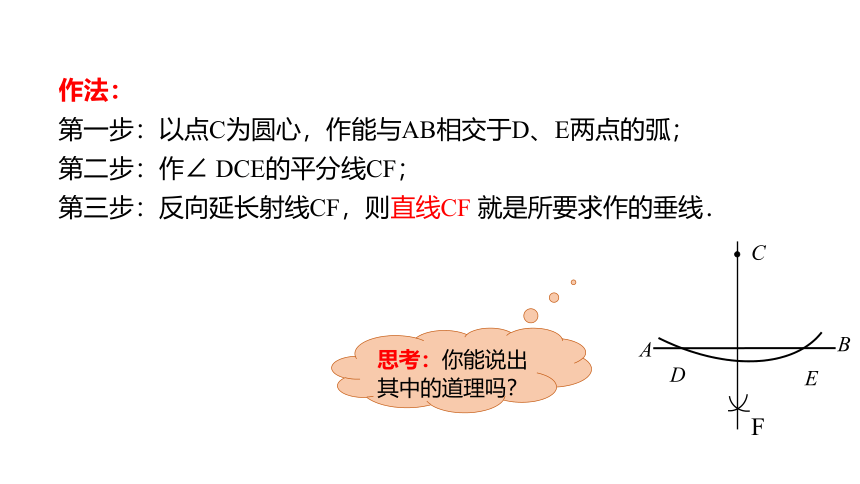
已知直线AB和AB外一点C,用直尺和圆规准确地经过点C作出直线AB的垂线.
分析:如图,若以点C为圆心,作能与直线AB相交于D E两点的弧,则CDE为等腰三角形,由“等腰三角形项角的平分线就是底边上的高”可知,只需作出∠DCE的平分线,则该平分线所在的直线就是要求作的垂线
作法:
第一步:以点C为圆心,作能与AB相交于D、E两点的弧;
第二步:作∠ DCE的平分线CF;
第三步:反向延长射线CF,则直线CF 就是所要求作的垂线.
A
B
C
D
E
思考:你能说出其中的道理吗?
F
作已知线段的垂直平分线
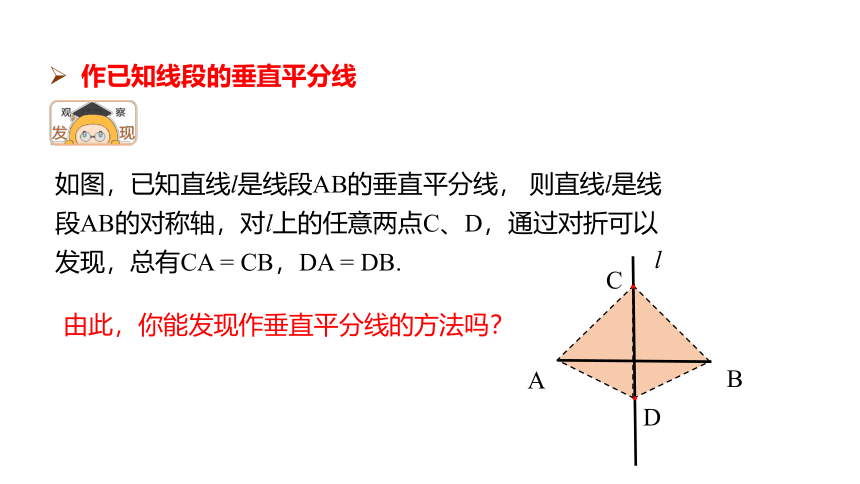
如图,已知直线l是线段AB的垂直平分线, 则直线l是线段AB的对称轴,对l上的任意两点C、D,通过对折可以发现,总有CA = CB,DA = DB.
C
A
D
B
l
.
.
由此,你能发现作垂直平分线的方法吗?
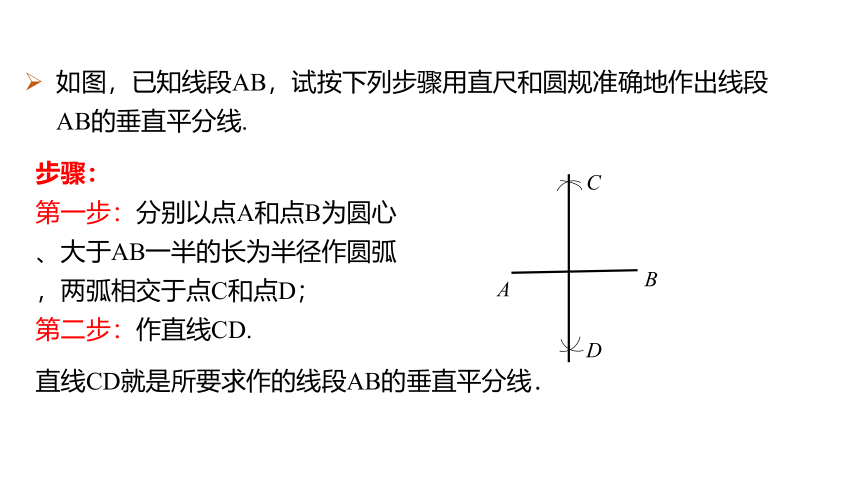
如图,已知线段AB,试按下列步骤用直尺和圆规准确地作出线段AB的垂直平分线.
步骤:
第一步:分别以点A和点B为圆心、大于AB一半的长为半径作圆弧,两弧相交于点C和点D;
第二步:作直线CD.
C
A
B
D
直线CD就是所要求作的线段AB的垂直平分线.
提示:作已知线段的垂直平分线的理论依据:三角形全等的判定方法——“S.S.S.”及等腰三角形的“三线合一”.
证明:如图,连结CA、CB、DA、DB.
∵AC=BC,AD=BD,CD=CD,∴△ACD≌△BCD(S.S.S.).
∴∠ACD=∠BCD(全等三角形的对应角相等).
∴CD垂直平分线段AB(等腰三角形的“三线合一”).
C
A
B
D
为什么CD是线段AB的垂直平分线呢?你能给出证明吗?
通过上面的作图,你还能发现什么?你会作任意一个三角形的三条中线吗?
通过作图,知道直线CD与线段AB的交点就是AB的中点,因此我们可以用这种方法作出线段AB的中点,从而可以作出任意一个三角形的的三条中线
例1 利用直尺和圆规作一个等于45°的角.
作法:
例题讲解
1. 作直线AB;
2. 过点A作直线AB的垂线AC ;
3. 作∠CAB 的平分线AD.
∠DAB就是要求作的角(如图所示)
例2 如图,点P在∠O的一边上,试过点P作∠O两边的垂线.
解:如图所示
作法:(1)以点P为圆心,适当长为半径画弧,交点P所在边于点A,B;(2)分别以A,B为圆心,大于 AB长为半径画弧,两弧相交于点A'; (3)过A',P两点作直线l1就是该边的垂线.
作法:
(4)以点P为圆心,适当长为半径画弧
交∠0的另一边于点C,D;
(5)分别以点C,D为圆心,大于 CD长为半径画弧,在不同于点P的一侧,两弧相交于点B';
(6)过P, B'两点作直线l2就是∠o另一边的垂线.
1.尺规作图:经过已知直线外一点作这条直线的垂线,下列作图中正确的是( )
B
随堂演练
2. 如图,在△AEF中,尺规作图如下:分别以点E,F为圆心,大于 EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连结AO,则下列结论正确的是( )
A.AO平分∠EAF B.AO垂直平分EF
C.GH垂直平分EF D.GH平分AF
C
3. 如图,已知钝角三角形ABC,其中∠A是钝角,求作AC边上的中线BD和高BH.
解:如图所示.
4. 如图,已知点P和直线l,求作点P关于直线l的对称点P′.
解:如图所示.
作法:(1)过点P作直线l的垂线,垂足为点O;
(2)在线段PO的延长线上截取OP′=OP,则点P′就是
点P关于直线l的对称点.
5. 如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站,使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?
分析:增设的公共汽车站要满足到两个小区的路程一样长,应在线段AB的垂直平分线上,又要在公路边上,所以找到AB的垂直平分线与公路的交点便是.
A
B
公共汽车站
经过一已知点作已知直线的垂线
经过已知直线上一点作已知直线的垂线,实质是作一个平角的平分线,并将角的平分线反向延长.
经过已知直线外一点作已知直线的垂线,实质是作以直线外这一点为顶点,底在直线上的等腰三角形的顶角的平分线.
线段垂直平分线的尺规作图
作已知线段的垂直平分线理论依据是:判定三角形全等的“边边边”
课堂小结
13.4 第2课时作垂线和垂直平分线
第13章 全等三角形
1.回顾已经学过的基本作图有哪几种?
(1)作一条线段等于已知线段;
(2)作一个角等于已知角;
(3)作已知角的平分线.
2.点与直线的位置关系有几种情况?
(1)点在直线上;(2)点在直线外.
知识回顾
经过一点作已知直线的垂线
获取新知
如何经过一已知点作已知直线的垂线呢?
可分为两种情况来讨论:
经过已知直线上一点作已知直线的垂线.
经过已知直线外一点作已知直线的垂线.
经过一已知点作已知直线的垂线有可以分为几种情况?
经过已知直线上一点作已知直线的垂线
求作的垂线 .
A
B
C
已知直线AB和AB上一点C,用直尺和圆规准确地经过点C作出直线AB的垂线。
分析:如图,由于点C在直线AB上,因此所求作的垂线正好是平角ACB的平分线所在的直线.
平角ACB的平分线所在的直线
转化
作法:
第一步:作平角ACB的平分线CF;
第二步:反向延长射线CF.
直线CF就是所要求作的垂线.
D
C
A
B
经过已知直线外一点作已知直线的垂线
A
B
C
D
E
已知直线AB和AB外一点C,用直尺和圆规准确地经过点C作出直线AB的垂线.
分析:如图,若以点C为圆心,作能与直线AB相交于D E两点的弧,则CDE为等腰三角形,由“等腰三角形项角的平分线就是底边上的高”可知,只需作出∠DCE的平分线,则该平分线所在的直线就是要求作的垂线
作法:
第一步:以点C为圆心,作能与AB相交于D、E两点的弧;
第二步:作∠ DCE的平分线CF;
第三步:反向延长射线CF,则直线CF 就是所要求作的垂线.
A
B
C
D
E
思考:你能说出其中的道理吗?
F
作已知线段的垂直平分线
如图,已知直线l是线段AB的垂直平分线, 则直线l是线段AB的对称轴,对l上的任意两点C、D,通过对折可以发现,总有CA = CB,DA = DB.
C
A
D
B
l
.
.
由此,你能发现作垂直平分线的方法吗?
如图,已知线段AB,试按下列步骤用直尺和圆规准确地作出线段AB的垂直平分线.
步骤:
第一步:分别以点A和点B为圆心、大于AB一半的长为半径作圆弧,两弧相交于点C和点D;
第二步:作直线CD.
C
A
B
D
直线CD就是所要求作的线段AB的垂直平分线.
提示:作已知线段的垂直平分线的理论依据:三角形全等的判定方法——“S.S.S.”及等腰三角形的“三线合一”.
证明:如图,连结CA、CB、DA、DB.
∵AC=BC,AD=BD,CD=CD,∴△ACD≌△BCD(S.S.S.).
∴∠ACD=∠BCD(全等三角形的对应角相等).
∴CD垂直平分线段AB(等腰三角形的“三线合一”).
C
A
B
D
为什么CD是线段AB的垂直平分线呢?你能给出证明吗?
通过上面的作图,你还能发现什么?你会作任意一个三角形的三条中线吗?
通过作图,知道直线CD与线段AB的交点就是AB的中点,因此我们可以用这种方法作出线段AB的中点,从而可以作出任意一个三角形的的三条中线
例1 利用直尺和圆规作一个等于45°的角.
作法:
例题讲解
1. 作直线AB;
2. 过点A作直线AB的垂线AC ;
3. 作∠CAB 的平分线AD.
∠DAB就是要求作的角(如图所示)
例2 如图,点P在∠O的一边上,试过点P作∠O两边的垂线.
解:如图所示
作法:(1)以点P为圆心,适当长为半径画弧,交点P所在边于点A,B;(2)分别以A,B为圆心,大于 AB长为半径画弧,两弧相交于点A'; (3)过A',P两点作直线l1就是该边的垂线.
作法:
(4)以点P为圆心,适当长为半径画弧
交∠0的另一边于点C,D;
(5)分别以点C,D为圆心,大于 CD长为半径画弧,在不同于点P的一侧,两弧相交于点B';
(6)过P, B'两点作直线l2就是∠o另一边的垂线.
1.尺规作图:经过已知直线外一点作这条直线的垂线,下列作图中正确的是( )
B
随堂演练
2. 如图,在△AEF中,尺规作图如下:分别以点E,F为圆心,大于 EF的长为半径作弧,两弧相交于G,H两点,作直线GH,交EF于点O,连结AO,则下列结论正确的是( )
A.AO平分∠EAF B.AO垂直平分EF
C.GH垂直平分EF D.GH平分AF
C
3. 如图,已知钝角三角形ABC,其中∠A是钝角,求作AC边上的中线BD和高BH.
解:如图所示.
4. 如图,已知点P和直线l,求作点P关于直线l的对称点P′.
解:如图所示.
作法:(1)过点P作直线l的垂线,垂足为点O;
(2)在线段PO的延长线上截取OP′=OP,则点P′就是
点P关于直线l的对称点.
5. 如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站,使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?
分析:增设的公共汽车站要满足到两个小区的路程一样长,应在线段AB的垂直平分线上,又要在公路边上,所以找到AB的垂直平分线与公路的交点便是.
A
B
公共汽车站
经过一已知点作已知直线的垂线
经过已知直线上一点作已知直线的垂线,实质是作一个平角的平分线,并将角的平分线反向延长.
经过已知直线外一点作已知直线的垂线,实质是作以直线外这一点为顶点,底在直线上的等腰三角形的顶角的平分线.
线段垂直平分线的尺规作图
作已知线段的垂直平分线理论依据是:判定三角形全等的“边边边”
课堂小结
