华师大版数学八年级上册同步课件:13.5 第2课时 线段垂直平分线(共24张PPT)
文档属性
| 名称 | 华师大版数学八年级上册同步课件:13.5 第2课时 线段垂直平分线(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 402.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
13.5 第2课时 线段垂直平分线
第13章 全等三角形
生活中的数学
在某高速公路l的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?你的方案是什么
高 速 公 路
B
l
情景导入
A
这要用到垂直平分线的知识.怎么用呢?
获取新知
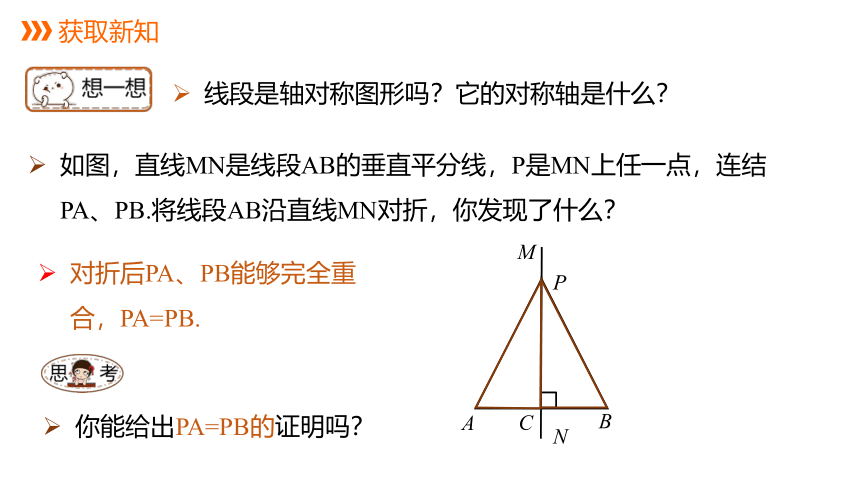
如图,直线MN是线段AB的垂直平分线,P是MN上任一点,连结PA、PB.将线段AB沿直线MN对折,你发现了什么?
M
N
P
A
C
B
对折后PA、PB能够完全重合,PA=PB.
线段是轴对称图形吗?它的对称轴是什么?
你能给出PA=PB的证明吗?
下面我们来证明刚才得到的结论:
段垂直平分线上的点到线段两端的距离相等.
M
N
P
A
C
B
已知:如图,MN丄AB,垂足为点C,AC =BC,点P是直线MN上的任意一点.
求证:PA=PB.
分析:图中有两个直角三角形APC和BPC,只要证明这两个三角形全等,便可证得PA=PB.
M
N
P
A
C
B
证明: ∵MN ⊥AB(已知),
∴∠ACP=∠BCP=90°(垂直的定义).
在△ACP和△BCP中,
∵
∴ △ACP≌△BCP(S.A.S.).
∴PA=PB(全等三角形的对应边相等).
AC=BC,
∠ACP=∠BCP,
PC=PC,
线段垂直平分线的性质定理:
线段垂直平分线上的点到线段两端的距离相等;
条件:点在线段的垂直平分线上;
结论:这个点到线段两端的距离相等.
表达方式:
如图,l ⊥ AB,AC=BC,点P在l上,则AP=BP.
作用:可用来证明两线段相等.
M
N
P
A
C
B
l
是三角形全等思路的简化升级版
线段垂直平分线的判定
写出性质定理及其逆命题的条件和结论,你有什么发现?
条 件 结 论
性质定理
逆命题
一个点在线段的垂直平分线上
这个点到线段两端的距离相等
一个点到线段两端的距离相等
这个点在线段的垂直平分线上
线段垂直平分线的性质定理,条件和结论反过来会有什么结果呢?
这个逆命题是不是一个真命题?你能证明吗?
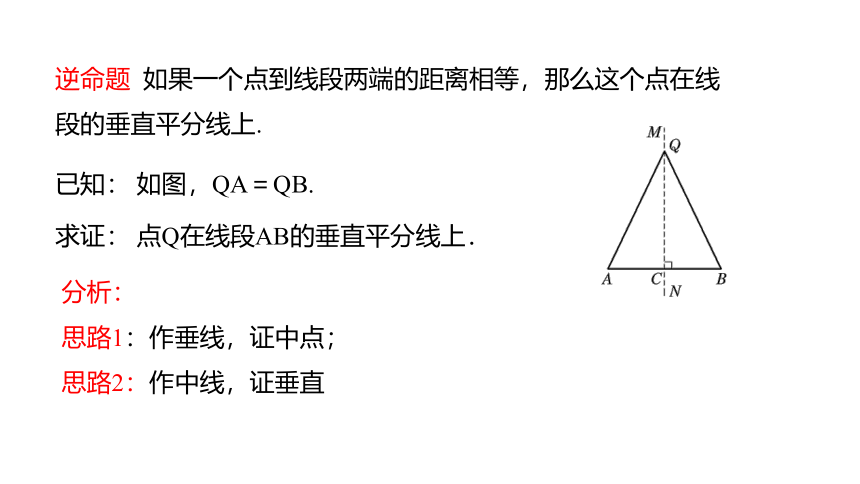
逆命题 如果一个点到线段两端的距离相等,那么这个点在线段的垂直平分线上.
已知: 如图,QA=QB.
求证: 点Q在线段AB的垂直平分线上.
分析:
思路1:作垂线,证中点;
思路2:作中线,证垂直
证明:过点Q作MN⊥AB,垂足为点C,
故∠QCA=∠QCB=90°.
在Rt△QCA 和Rt△QCB中,
∵QA=QB,QC=QC,
∴Rt△QCA≌Rt△QCB(H.L.).
∴AC=BC.
∴点Q在线段AB的垂直平分线上.
已知: 如图,QA=QB.
求证: 点Q在线段AB的垂直平分线上.
你能写出后一种添加辅助线的证明过程吗?
到线段两端距离相等的点在线段的垂直平分线上.
条件:点到线段两端距离相等;
结论:点在线段垂直平分线上.
表达方式:如图,∵PA=PB,
∴点P在线段AB的垂直平分线上.
作用:①作线段的垂直平分线的依据;
②可用来证线段垂直、相等.
线段垂直平分线的判定定理:
拓展:三角形三边的垂直平分线交于一点,这点到三角形的三个顶点的距离相等,这个点叫这个三角形的外心.
点拨:三线交于一点,只需证明第三条经过另外两条的交点思路可表示如下:
l是AB的垂直平分线
m是BC的垂直平分线
OA=OB
OB=OC
OA=OC
点O在AC的垂直平分线上
B
C
A
O
l
n
m
试试看,你会写出证明过程吗?
你能给出三角形三边的垂直平分线交于一点的证明吗?
证明:连接OA,OB,OC.
∵点O在AB,AC的垂直平分线上,
∴OA=OB,OA=OC (线段垂直平分线上 的点到线段两端距离相等).
∴OB=OC.
∴点O在BC的垂直平分线上 (到线段两端距离相等的点在线段的垂直平分线上).
B
C
A
O
l
n
m
例1 如图,在△ABC中,AC=5,AB的垂直平分线DE分别交
AB,AC于点E,D,
(1)若△BCD的周长为8,求BC的长;
(2)若BC=4,求△BCD的周长.
导引:由DE是AB的垂直平分线,得AD=BD,所以BD与CD的长度和等于AC的长,
例题讲解
解:∵DE是AB的垂直平分线,∴AD=BD,
∴BD+CD=AD+CD=AC=5.
(1)∵△BCD的周长为8,
∴BC=△BCD的周长-(BD+CD)=8-5=3.
(2)∵BC=4,
∴△BCD的周长=BC+BD+CD=5+4=9.
利用线段垂直平分 线的性质转化线段的位 置,是一种常用的解题 方法.本题中解题的关 键是利用线段垂直平分 线的性质将CD 的长转 化为BD的长,从而将 △ ACD 的周长转化为线 段AB+AC的长,进行求解.
例2 如图,在△ABC中,∠ACB=90°,AD平分
∠BAC,DE⊥AB于E.求证:直线AD是CE的垂直平分线.
只需要证明存在两点即可
证明:∵AD平分∠BAC,
∴∠DAE=∠DAC.
∵DE⊥AB,
∴∠AED=90°,
∴∠AED=∠ACB,
在△ADE和△ADC中
∠DAE=∠DAC.
∵ ∠AED=∠ACB,
AD=AD,
∴△ADE≌△ADC
∴CD=DE,AC=AE,
∴点D在CE的垂直平分线上;
点A也在CE的垂直平分线上,
∴直线AD是CE的垂直平分线.
判断线段垂直平分线的两种方法:
一是定义法,二是判定定理 . 一般习惯用定义法 进行判断,而利用判定定理 判断更简单 . 用判定定理判 定一条直线是线段的垂直平分线时,一定要证明直线上 有两点到线段两个端点的距离相等 .
1. 如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为( )
A.6
B.5
C.4
D.3
B
随堂演练
2. 如图,已知线段AB,BC的垂直平分线l1,l2交于点M,则线段AM,CM的大小关系是( )
A.AM>CM
B.AM=CM
C.AMD.无法确定
B
3. 如图,点D在△ABC的BC边上,且BC=BD+AD,则点D在线段( )的垂直平分线上.
A.AB
B.AC
C.BC
D.不确定
B
4.如图,△ABC中,AB=AC,AB的垂直平分线交交AC于E,连接BE,AB+BC=16cm,则△BCE的周长是 cm.
A
B
C
D
E
16
5. 如图,已知AB=AD,BC=DC,E是AC上一点,
求证:(1)BE=DE;(2)∠ABE=∠ADE.
证明:(1)连结BD,如图,
∵AB=AD,BC=CD,
∴A,C两点均在线段BD的垂直平分线上.
∴AC是线段BD的垂直平分线.
又∵E是AC上一点,
∴BE=DE.
证明:(2)在△ABE和△ADE中,
∵AB=AD,BE=DE,AE=AE,
∴△ABE≌△ADE,
∴∠ABE=∠ADE.
证明两条线段或两个角相等 常用方法:
1. 通过证明两条线段所在的 三角形全等;
2. 用线段垂直平分线的性质 证明两条线段相等;
3. 用轴对称图形的对应元素 证明 .
线段的垂直平分的性质和判定
性质
到线段两端点距离相等的点在线段的垂直平分线上
内容
判定
内容
作用
线段垂直平分线上的点到线段的两个端点的距离相等
作用
见垂直平分线,得线段相等
判断一个点是否在线段的垂直平分线上
课堂小结
13.5 第2课时 线段垂直平分线
第13章 全等三角形
生活中的数学
在某高速公路l的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?你的方案是什么
高 速 公 路
B
l
情景导入
A
这要用到垂直平分线的知识.怎么用呢?
获取新知
如图,直线MN是线段AB的垂直平分线,P是MN上任一点,连结PA、PB.将线段AB沿直线MN对折,你发现了什么?
M
N
P
A
C
B
对折后PA、PB能够完全重合,PA=PB.
线段是轴对称图形吗?它的对称轴是什么?
你能给出PA=PB的证明吗?
下面我们来证明刚才得到的结论:
段垂直平分线上的点到线段两端的距离相等.
M
N
P
A
C
B
已知:如图,MN丄AB,垂足为点C,AC =BC,点P是直线MN上的任意一点.
求证:PA=PB.
分析:图中有两个直角三角形APC和BPC,只要证明这两个三角形全等,便可证得PA=PB.
M
N
P
A
C
B
证明: ∵MN ⊥AB(已知),
∴∠ACP=∠BCP=90°(垂直的定义).
在△ACP和△BCP中,
∵
∴ △ACP≌△BCP(S.A.S.).
∴PA=PB(全等三角形的对应边相等).
AC=BC,
∠ACP=∠BCP,
PC=PC,
线段垂直平分线的性质定理:
线段垂直平分线上的点到线段两端的距离相等;
条件:点在线段的垂直平分线上;
结论:这个点到线段两端的距离相等.
表达方式:
如图,l ⊥ AB,AC=BC,点P在l上,则AP=BP.
作用:可用来证明两线段相等.
M
N
P
A
C
B
l
是三角形全等思路的简化升级版
线段垂直平分线的判定
写出性质定理及其逆命题的条件和结论,你有什么发现?
条 件 结 论
性质定理
逆命题
一个点在线段的垂直平分线上
这个点到线段两端的距离相等
一个点到线段两端的距离相等
这个点在线段的垂直平分线上
线段垂直平分线的性质定理,条件和结论反过来会有什么结果呢?
这个逆命题是不是一个真命题?你能证明吗?
逆命题 如果一个点到线段两端的距离相等,那么这个点在线段的垂直平分线上.
已知: 如图,QA=QB.
求证: 点Q在线段AB的垂直平分线上.
分析:
思路1:作垂线,证中点;
思路2:作中线,证垂直
证明:过点Q作MN⊥AB,垂足为点C,
故∠QCA=∠QCB=90°.
在Rt△QCA 和Rt△QCB中,
∵QA=QB,QC=QC,
∴Rt△QCA≌Rt△QCB(H.L.).
∴AC=BC.
∴点Q在线段AB的垂直平分线上.
已知: 如图,QA=QB.
求证: 点Q在线段AB的垂直平分线上.
你能写出后一种添加辅助线的证明过程吗?
到线段两端距离相等的点在线段的垂直平分线上.
条件:点到线段两端距离相等;
结论:点在线段垂直平分线上.
表达方式:如图,∵PA=PB,
∴点P在线段AB的垂直平分线上.
作用:①作线段的垂直平分线的依据;
②可用来证线段垂直、相等.
线段垂直平分线的判定定理:
拓展:三角形三边的垂直平分线交于一点,这点到三角形的三个顶点的距离相等,这个点叫这个三角形的外心.
点拨:三线交于一点,只需证明第三条经过另外两条的交点思路可表示如下:
l是AB的垂直平分线
m是BC的垂直平分线
OA=OB
OB=OC
OA=OC
点O在AC的垂直平分线上
B
C
A
O
l
n
m
试试看,你会写出证明过程吗?
你能给出三角形三边的垂直平分线交于一点的证明吗?
证明:连接OA,OB,OC.
∵点O在AB,AC的垂直平分线上,
∴OA=OB,OA=OC (线段垂直平分线上 的点到线段两端距离相等).
∴OB=OC.
∴点O在BC的垂直平分线上 (到线段两端距离相等的点在线段的垂直平分线上).
B
C
A
O
l
n
m
例1 如图,在△ABC中,AC=5,AB的垂直平分线DE分别交
AB,AC于点E,D,
(1)若△BCD的周长为8,求BC的长;
(2)若BC=4,求△BCD的周长.
导引:由DE是AB的垂直平分线,得AD=BD,所以BD与CD的长度和等于AC的长,
例题讲解
解:∵DE是AB的垂直平分线,∴AD=BD,
∴BD+CD=AD+CD=AC=5.
(1)∵△BCD的周长为8,
∴BC=△BCD的周长-(BD+CD)=8-5=3.
(2)∵BC=4,
∴△BCD的周长=BC+BD+CD=5+4=9.
利用线段垂直平分 线的性质转化线段的位 置,是一种常用的解题 方法.本题中解题的关 键是利用线段垂直平分 线的性质将CD 的长转 化为BD的长,从而将 △ ACD 的周长转化为线 段AB+AC的长,进行求解.
例2 如图,在△ABC中,∠ACB=90°,AD平分
∠BAC,DE⊥AB于E.求证:直线AD是CE的垂直平分线.
只需要证明存在两点即可
证明:∵AD平分∠BAC,
∴∠DAE=∠DAC.
∵DE⊥AB,
∴∠AED=90°,
∴∠AED=∠ACB,
在△ADE和△ADC中
∠DAE=∠DAC.
∵ ∠AED=∠ACB,
AD=AD,
∴△ADE≌△ADC
∴CD=DE,AC=AE,
∴点D在CE的垂直平分线上;
点A也在CE的垂直平分线上,
∴直线AD是CE的垂直平分线.
判断线段垂直平分线的两种方法:
一是定义法,二是判定定理 . 一般习惯用定义法 进行判断,而利用判定定理 判断更简单 . 用判定定理判 定一条直线是线段的垂直平分线时,一定要证明直线上 有两点到线段两个端点的距离相等 .
1. 如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为( )
A.6
B.5
C.4
D.3
B
随堂演练
2. 如图,已知线段AB,BC的垂直平分线l1,l2交于点M,则线段AM,CM的大小关系是( )
A.AM>CM
B.AM=CM
C.AM
B
3. 如图,点D在△ABC的BC边上,且BC=BD+AD,则点D在线段( )的垂直平分线上.
A.AB
B.AC
C.BC
D.不确定
B
4.如图,△ABC中,AB=AC,AB的垂直平分线交交AC于E,连接BE,AB+BC=16cm,则△BCE的周长是 cm.
A
B
C
D
E
16
5. 如图,已知AB=AD,BC=DC,E是AC上一点,
求证:(1)BE=DE;(2)∠ABE=∠ADE.
证明:(1)连结BD,如图,
∵AB=AD,BC=CD,
∴A,C两点均在线段BD的垂直平分线上.
∴AC是线段BD的垂直平分线.
又∵E是AC上一点,
∴BE=DE.
证明:(2)在△ABE和△ADE中,
∵AB=AD,BE=DE,AE=AE,
∴△ABE≌△ADE,
∴∠ABE=∠ADE.
证明两条线段或两个角相等 常用方法:
1. 通过证明两条线段所在的 三角形全等;
2. 用线段垂直平分线的性质 证明两条线段相等;
3. 用轴对称图形的对应元素 证明 .
线段的垂直平分的性质和判定
性质
到线段两端点距离相等的点在线段的垂直平分线上
内容
判定
内容
作用
线段垂直平分线上的点到线段的两个端点的距离相等
作用
见垂直平分线,得线段相等
判断一个点是否在线段的垂直平分线上
课堂小结
