华师大版数学八年级上册同步课件:14.2 第1课时 勾股定理在现实生活中的应用(共12张PPT)
文档属性
| 名称 | 华师大版数学八年级上册同步课件:14.2 第1课时 勾股定理在现实生活中的应用(共12张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 341.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 21:00:13 | ||
图片预览



文档简介
(共12张PPT)
14.2 第1课时 勾股定理在现实生活中的应用
第14章 勾股定理
情景导入
折竹抵地(源自《九章算术》):今有竹高一丈,风折抵地,去本三尺.问折者高几何
竹子折成的两段和地面上竹根和竹梢的接地点连接的线段构成一个什么样的三角形?
直角三角形
勾股定理能解决直角三角形的许多问题,因此在现实生活和数学中有着广泛的应用.
大意:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处距离原竹子底部3尺远.问原来的竹子有多高
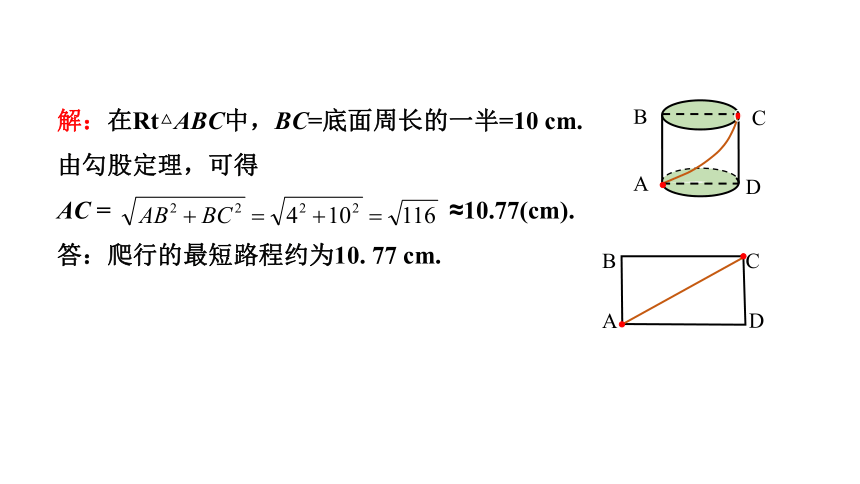
例1 如图,一圆柱体的底面周长为20 cm, 高AB为4 cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短 路程.(精确到0.01 cm)
最短距离问题
分析:蚂蚁实际上是在圆柱的半个侧面内爬动,如果将这半个侧面展开,得到长方形ABCD,根据“两点之间,线段最短”,所求的最短路程就是这一展开图——长方形ABCD的对角线AC之长.
例题讲解
B
C
A
D
C
A
B
0
D
解:在Rt△ABC中,BC=底面周长的一半=10 cm.
由勾股定理,可得
AC = ≈10.77(cm).
答:爬行的最短路程约为10. 77 cm.
B
C
A
D
C
A
B
0
D
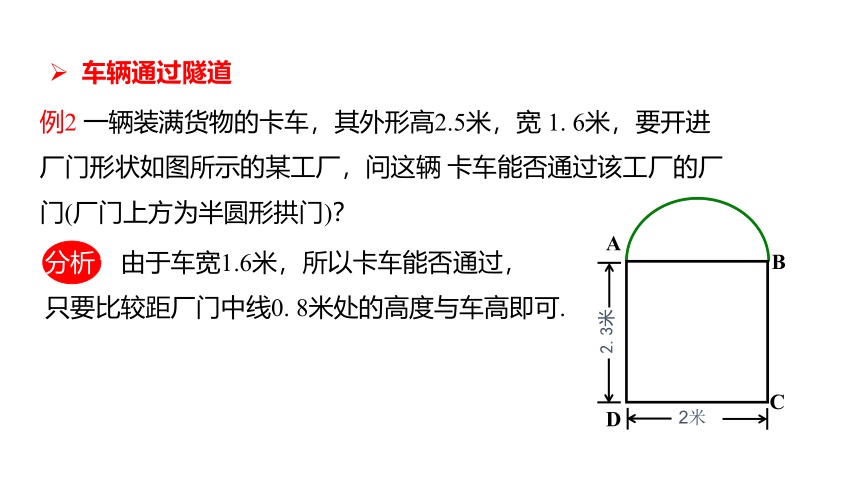
例2 一辆装满货物的卡车,其外形高2.5米,宽 1. 6米,要开进厂门形状如图所示的某工厂,问这辆 卡车能否通过该工厂的厂门(厂门上方为半圆形拱门)?
分析:由于车宽1.6米,所以卡车能否通过,
只要比较距厂门中线0. 8米处的高度与车高即可.
车辆通过隧道
A
B
C
D
2米
2.3米
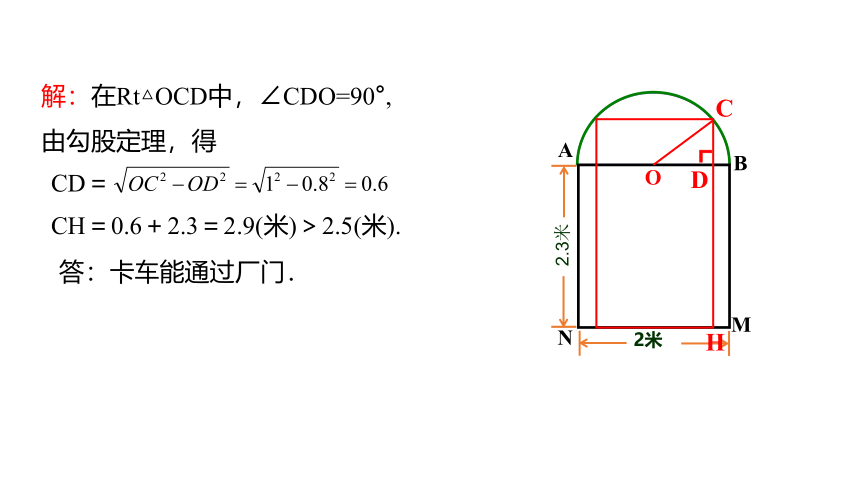
CD=
CH=0.6+2.3=2.9(米)>2.5(米).
答:卡车能通过厂门.
解:在Rt△OCD中,∠CDO=90°,
由勾股定理,得
A
B
M
N
O
C
┏
D
H
2米
2.3米
1. 如果梯子的底端离建筑物9m,那么15m长的梯子可以到达建筑物的高度是( )
A.10 m B.11 m C.12 m D.13 m
C
随堂演练
2. 如图,若圆柱的底面周长是30 cm,高是40 cm,从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处做装饰,则这条丝线的最小长度是( )
A.80 cm B.70 cm
C.60 cm D.50 cm
D
3. 某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境.已知这种草皮每平方米售价a元,则购买这种草皮至少需要______元.
60a
4. 假设小汽车在城市街道上的行驶速度不得超过70千米/时,如图,一辆小汽车在一条城市街道上沿直线行驶,某一时刻刚好行驶到路面车速检测仪A的正前方30米的C处,过了2秒后,测得小汽车在与车速检测仪距离为50米的B处,那么这辆小汽车超速了吗?
解:根据题意,得AC=30米,AB=50米,∠C=90°.
在Rt△ACB中,根据勾股定理,得BC= =40(米),
小汽车2秒行驶了40米,则1小时行驶40×30×60=72000(米),
即小汽车的行驶速度为72千米/时.
因为72>70,
所以这辆小汽车超速了.
勾股定理的应用
最短路程问题
过隧道问题
课堂小结
14.2 第1课时 勾股定理在现实生活中的应用
第14章 勾股定理
情景导入
折竹抵地(源自《九章算术》):今有竹高一丈,风折抵地,去本三尺.问折者高几何
竹子折成的两段和地面上竹根和竹梢的接地点连接的线段构成一个什么样的三角形?
直角三角形
勾股定理能解决直角三角形的许多问题,因此在现实生活和数学中有着广泛的应用.
大意:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处距离原竹子底部3尺远.问原来的竹子有多高
例1 如图,一圆柱体的底面周长为20 cm, 高AB为4 cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短 路程.(精确到0.01 cm)
最短距离问题
分析:蚂蚁实际上是在圆柱的半个侧面内爬动,如果将这半个侧面展开,得到长方形ABCD,根据“两点之间,线段最短”,所求的最短路程就是这一展开图——长方形ABCD的对角线AC之长.
例题讲解
B
C
A
D
C
A
B
0
D
解:在Rt△ABC中,BC=底面周长的一半=10 cm.
由勾股定理,可得
AC = ≈10.77(cm).
答:爬行的最短路程约为10. 77 cm.
B
C
A
D
C
A
B
0
D
例2 一辆装满货物的卡车,其外形高2.5米,宽 1. 6米,要开进厂门形状如图所示的某工厂,问这辆 卡车能否通过该工厂的厂门(厂门上方为半圆形拱门)?
分析:由于车宽1.6米,所以卡车能否通过,
只要比较距厂门中线0. 8米处的高度与车高即可.
车辆通过隧道
A
B
C
D
2米
2.3米
CD=
CH=0.6+2.3=2.9(米)>2.5(米).
答:卡车能通过厂门.
解:在Rt△OCD中,∠CDO=90°,
由勾股定理,得
A
B
M
N
O
C
┏
D
H
2米
2.3米
1. 如果梯子的底端离建筑物9m,那么15m长的梯子可以到达建筑物的高度是( )
A.10 m B.11 m C.12 m D.13 m
C
随堂演练
2. 如图,若圆柱的底面周长是30 cm,高是40 cm,从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处做装饰,则这条丝线的最小长度是( )
A.80 cm B.70 cm
C.60 cm D.50 cm
D
3. 某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境.已知这种草皮每平方米售价a元,则购买这种草皮至少需要______元.
60a
4. 假设小汽车在城市街道上的行驶速度不得超过70千米/时,如图,一辆小汽车在一条城市街道上沿直线行驶,某一时刻刚好行驶到路面车速检测仪A的正前方30米的C处,过了2秒后,测得小汽车在与车速检测仪距离为50米的B处,那么这辆小汽车超速了吗?
解:根据题意,得AC=30米,AB=50米,∠C=90°.
在Rt△ACB中,根据勾股定理,得BC= =40(米),
小汽车2秒行驶了40米,则1小时行驶40×30×60=72000(米),
即小汽车的行驶速度为72千米/时.
因为72>70,
所以这辆小汽车超速了.
勾股定理的应用
最短路程问题
过隧道问题
课堂小结
