华师大版数学八年级上册同步课件:14.2 第2课时 勾股定理在数学中的应用(共16张PPT)
文档属性
| 名称 | 华师大版数学八年级上册同步课件:14.2 第2课时 勾股定理在数学中的应用(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 303.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 21:01:35 | ||
图片预览






文档简介
(共16张PPT)
14.2 第2课时 勾股定理在数学中的应用
第14章 勾股定理
情景导入
一个三角形的三边长分别是15 cm, 20 cm,25 cm,则这个三角形的面积是( )
A.250cm2 B.150cm2 C.200cm2 D.不能确定
解析 : 152+ 202=252,.此三角形为直角三角形,S=15 ×20 = 150(cm2).
B
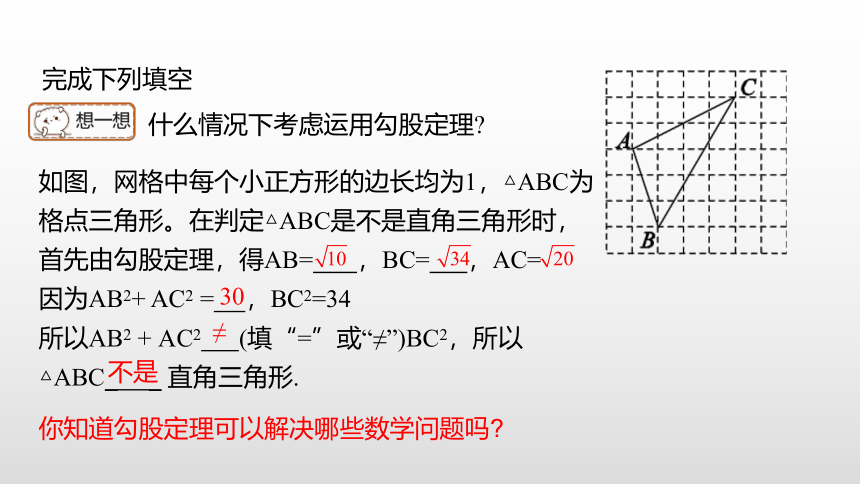
如图,网格中每个小正方形的边长均为1,△ABC为格点三角形。在判定△ABC是不是直角三角形时,首先由勾股定理,得AB= ,BC= ,AC= 因为AB2+ AC2 = ,BC2=34
所以AB2 + AC2 (填“=”或“≠”)BC2,所以△ABC_ _ 直角三角形.
完成下列填空
什么情况下考虑运用勾股定理
30
≠
不是
你知道勾股定理可以解决哪些数学问题吗
在直角三角形中,已知任意两边长,利用勾股定理可求第三边长.有时不是已知直角三角形的两边长,而是已知一边长和另两边长的关系,或者已知三边长的关系要求每一条边长,则常需要设未知数,再结合勾股定理列方程.
知识点一:常规计算型立即体验
获取新知
把勾股定理与平方差公式、两数和(差)的平方公式、方程和轴对称等相结合,运用数形结合思想可以解决许多难度较大的综合型题目,在几何图形中,创造条件,把非直角三角形转化为直角三角形则是解决问题之根本.
知识点二:综合型
获取新知
例1 如图,有一张直角三角形纸片,两直角边AC=6 cm,BC=8cm,现将直角边AC沿AD折叠,使点C落在斜边AB上的点E处,试求CD的长.
知识点一:常规计算型立即体验
例题讲解
在Rt△ABC中,∵AC=6 cm,BC=8 cm,
∴AB2=AC2+BC2=62+82=100,∴AB=10(cm).
由折叠的性质,可知∠C=∠DEA=90°,AC=AE=6 cm,
故BE=10-6=4(cm).
设CD=x cm,则DE=x cm,BD=(8-x) cm.
在Rt△BDE中,由勾股定理,得x2+42=(8-x)2,
解得x=3.∴CD的长为3 cm.
解:
知识点一:常规计算型立即体验
例题讲解
关于折叠问题,要紧扣折叠前后的对应边相等、对应角相等;其解题步骤为:
①利用重合的图形传递数据(一般不用重合的图形进行计算);②选择直角三角形,这个直角三角形一般已知一边,另两边可通过重合图形找到数量关系,利用勾股定理列方程求解.
方法点拨
例2 如图,已知CD=6cm,AD=8cm, ∠ADC=90o,BC=24cm,AB=26cm,求阴影部分面积.
知识点二:综合型
解:在 Rt △ADC中,
∵AC2 = AD2 + CD2 (勾股定理)
=82 + 62 = 100,
∴AC = 10.
∵ AC2 + BC2 = 102 + 242 = 676 = 262 = AB2,
∴ △ACB为直角三角形(勾股定理的逆定理),
∴ S阴影部分= S△ACB - S △ACD = ×10 ×24 - ×6×8 =96(m2).
知识点二:综合型
例3 如图,在3 ×3的方格图中,每个小方格的边长都为1,请在给定网格中按下列要求画出 图形:
(1)画出所有从点A出发,另一个端点在格点(即小正方形的顶点)上,且长度为 的线段;
(2) 画出所有以题(1)中所画线段为腰的等腰三 角形.
其他数学问题
A
解:(1)如图,AB、AC、AE、AD的长度均为
(2)图中,△ABC、 △ABE 、 △ABD 、
△ACE、 △ACD、△AED就是所要画的等腰三角形.
A
D
E
C
B
1. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,以点A为圆心,AC长为半径画弧,交AB于点D,则BD=_____.
4
随堂演练
2. 直角三角形的两条直角边的长分别为9 cm和12 cm,则它斜边上的高为 ( )
A.6 cm B.8 cm C. cm D. cm
D
3.如图所示,在△ABC中,AB=5cm,BC=6cm, BC边上的中线AD=4 cm,求△ABC的面积.
解:∵AD是BC边上的中线,∴BD= BC=3 cm.
∵AD2+BD2=42+32=25,AB2=52=25,
∴AD2+BD2=AB2,
∴△ABD是直角三角形,且∠ADB=90°,
∴S△ABC= BC·AD= ×6×4=12(cm2).
勾股定理在数学中的应用
求线段的长
利用勾股定理求面积
课堂小结
14.2 第2课时 勾股定理在数学中的应用
第14章 勾股定理
情景导入
一个三角形的三边长分别是15 cm, 20 cm,25 cm,则这个三角形的面积是( )
A.250cm2 B.150cm2 C.200cm2 D.不能确定
解析 : 152+ 202=252,.此三角形为直角三角形,S=15 ×20 = 150(cm2).
B
如图,网格中每个小正方形的边长均为1,△ABC为格点三角形。在判定△ABC是不是直角三角形时,首先由勾股定理,得AB= ,BC= ,AC= 因为AB2+ AC2 = ,BC2=34
所以AB2 + AC2 (填“=”或“≠”)BC2,所以△ABC_ _ 直角三角形.
完成下列填空
什么情况下考虑运用勾股定理
30
≠
不是
你知道勾股定理可以解决哪些数学问题吗
在直角三角形中,已知任意两边长,利用勾股定理可求第三边长.有时不是已知直角三角形的两边长,而是已知一边长和另两边长的关系,或者已知三边长的关系要求每一条边长,则常需要设未知数,再结合勾股定理列方程.
知识点一:常规计算型立即体验
获取新知
把勾股定理与平方差公式、两数和(差)的平方公式、方程和轴对称等相结合,运用数形结合思想可以解决许多难度较大的综合型题目,在几何图形中,创造条件,把非直角三角形转化为直角三角形则是解决问题之根本.
知识点二:综合型
获取新知
例1 如图,有一张直角三角形纸片,两直角边AC=6 cm,BC=8cm,现将直角边AC沿AD折叠,使点C落在斜边AB上的点E处,试求CD的长.
知识点一:常规计算型立即体验
例题讲解
在Rt△ABC中,∵AC=6 cm,BC=8 cm,
∴AB2=AC2+BC2=62+82=100,∴AB=10(cm).
由折叠的性质,可知∠C=∠DEA=90°,AC=AE=6 cm,
故BE=10-6=4(cm).
设CD=x cm,则DE=x cm,BD=(8-x) cm.
在Rt△BDE中,由勾股定理,得x2+42=(8-x)2,
解得x=3.∴CD的长为3 cm.
解:
知识点一:常规计算型立即体验
例题讲解
关于折叠问题,要紧扣折叠前后的对应边相等、对应角相等;其解题步骤为:
①利用重合的图形传递数据(一般不用重合的图形进行计算);②选择直角三角形,这个直角三角形一般已知一边,另两边可通过重合图形找到数量关系,利用勾股定理列方程求解.
方法点拨
例2 如图,已知CD=6cm,AD=8cm, ∠ADC=90o,BC=24cm,AB=26cm,求阴影部分面积.
知识点二:综合型
解:在 Rt △ADC中,
∵AC2 = AD2 + CD2 (勾股定理)
=82 + 62 = 100,
∴AC = 10.
∵ AC2 + BC2 = 102 + 242 = 676 = 262 = AB2,
∴ △ACB为直角三角形(勾股定理的逆定理),
∴ S阴影部分= S△ACB - S △ACD = ×10 ×24 - ×6×8 =96(m2).
知识点二:综合型
例3 如图,在3 ×3的方格图中,每个小方格的边长都为1,请在给定网格中按下列要求画出 图形:
(1)画出所有从点A出发,另一个端点在格点(即小正方形的顶点)上,且长度为 的线段;
(2) 画出所有以题(1)中所画线段为腰的等腰三 角形.
其他数学问题
A
解:(1)如图,AB、AC、AE、AD的长度均为
(2)图中,△ABC、 △ABE 、 △ABD 、
△ACE、 △ACD、△AED就是所要画的等腰三角形.
A
D
E
C
B
1. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,以点A为圆心,AC长为半径画弧,交AB于点D,则BD=_____.
4
随堂演练
2. 直角三角形的两条直角边的长分别为9 cm和12 cm,则它斜边上的高为 ( )
A.6 cm B.8 cm C. cm D. cm
D
3.如图所示,在△ABC中,AB=5cm,BC=6cm, BC边上的中线AD=4 cm,求△ABC的面积.
解:∵AD是BC边上的中线,∴BD= BC=3 cm.
∵AD2+BD2=42+32=25,AB2=52=25,
∴AD2+BD2=AB2,
∴△ABD是直角三角形,且∠ADB=90°,
∴S△ABC= BC·AD= ×6×4=12(cm2).
勾股定理在数学中的应用
求线段的长
利用勾股定理求面积
课堂小结
