勾股定理
图片预览


文档简介
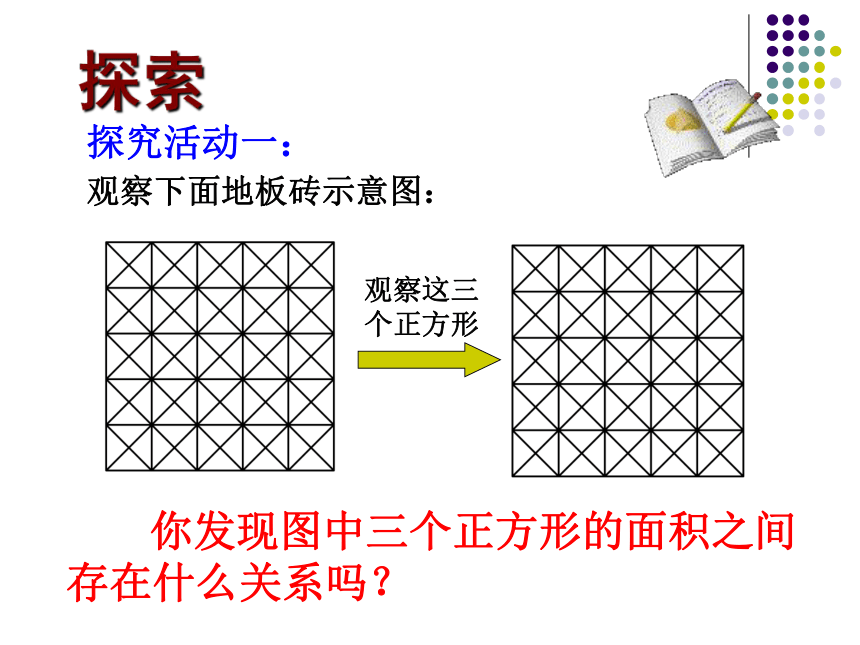
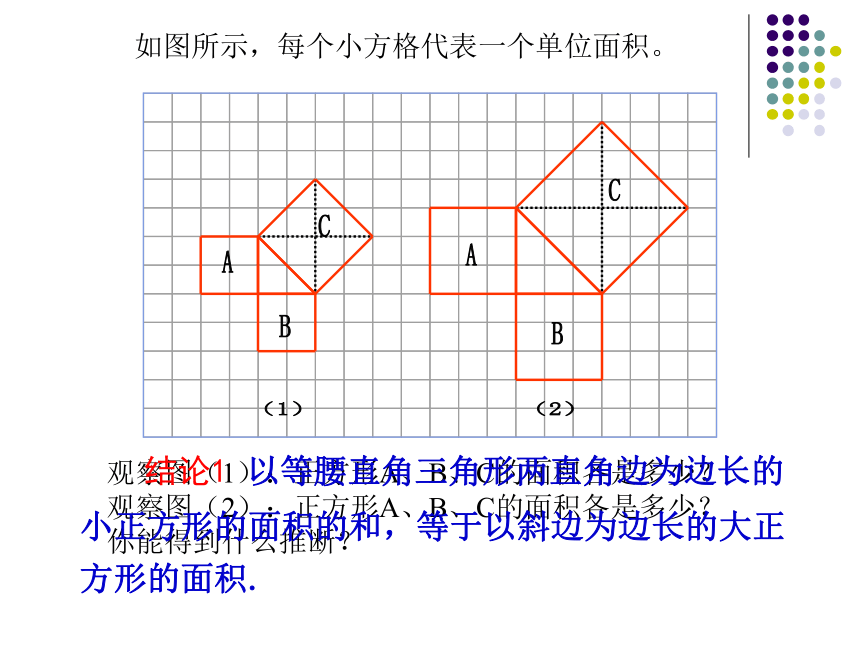
课件17张PPT。这就是本届大会会徽的图案.你见过这个图案吗?你听说过勾股定理吗? 这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”.八年级数学(下册)?人教版 18.1勾股定理第1课时探究活动一: 观察下面地板砖示意图:探索观察这三个正方形 你发现图中三个正方形的面积之间存在什么关系吗?如图所示,每个小方格代表一个单位面积。观察图(1):正方形A、B、C的面积各是多少?
观察图(2):正方形A、B、C的面积各是多少?
你能得到什么推断?
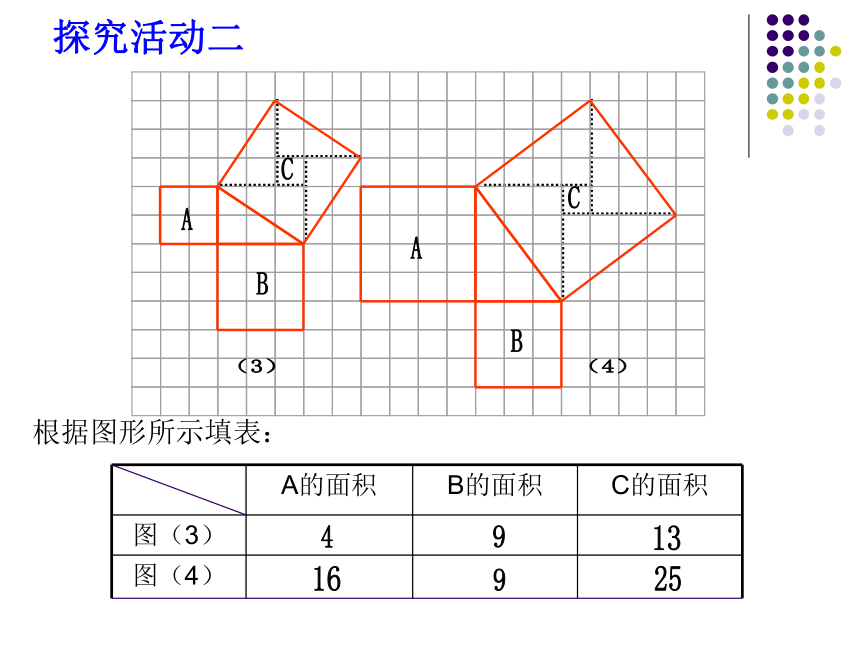
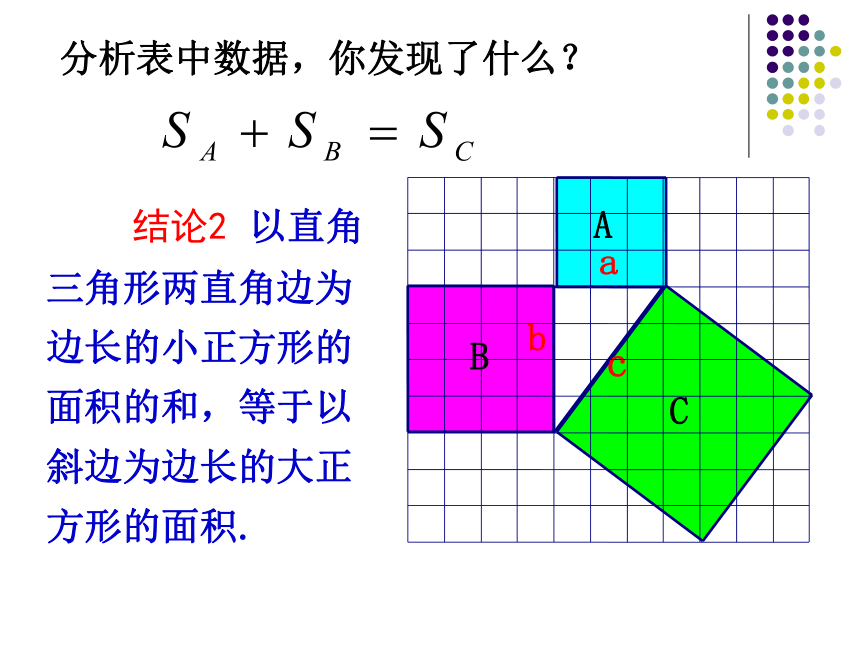
结论1 以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的大正方形的面积.根据图形所示填表:探究活动二分析表中数据,你发现了什么? 结论2 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的大正方形的面积.练习:
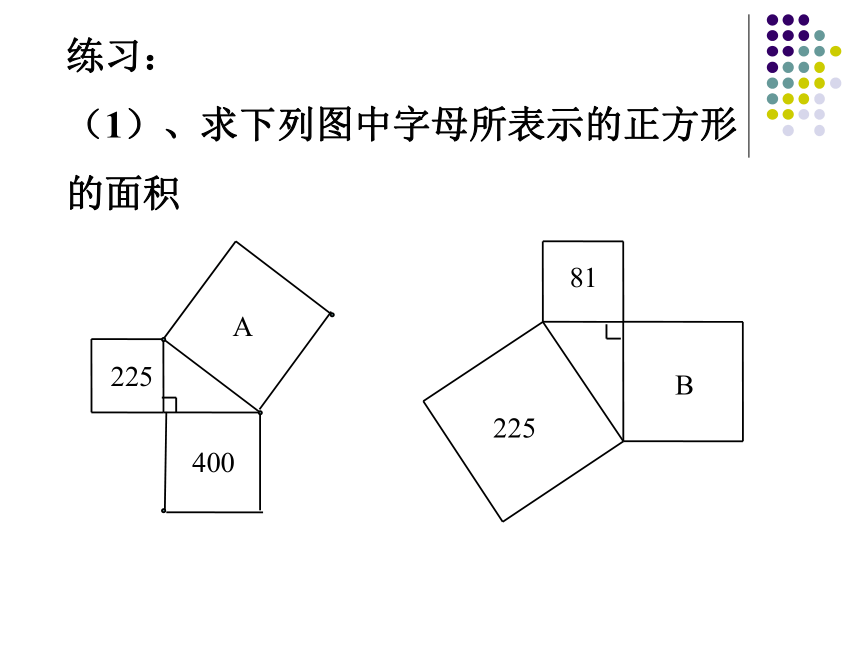
(1)、求下列图中字母所表示的正方形
的面积 (2)你能发现直角三角形三边长度之间
存在什么关系吗? (3)分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度. (2)中的规律对这个三角形仍然成立吗?动手实践 直角三角形两直角边的平方和等于斜边的平方. 如果直角三角形两直角边分别为a,b,斜边为c,那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方. 勾股定理a2 + b2 =c2
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦,“勾股定理”因此而得名. (在西方称为毕达哥拉斯定理)数学小史中国古代数学家——赵爽的验证方法 还可以认为是四个直角三角形与一个小正方形面积的和,即∴2002年在北京召开的国际数学家大会的会标就是依据我国古代数学家赵爽的弦图制作的。∴ ∵正方形ABCD的面积为c2例. 一架高为10米的木梯,架在高为8米的墙上(如图),这时梯脚与墙的距离是多少米? ABC解:∵在直角?ABC中,∠C=90°
∴ 根据勾股定理得
BC2 + AC2 = AB2
又∵AC=8 米 AB=10米
∴BC= AB2—AC2
= 102 — 82
= 6 米基础巩固练习:
1.填空: (1)直角?ABC的两条直角边a=3, b=4,则斜边c = 。 (2). 一个三角形的三个内角之比为1:2:3,则此三角形是___,若这三个角所对的边分别为a,b,c,则它们的关系是____. 2.求出下列直角三角形中未知边的长度收获的喜悦 勾股定理从边的角度刻画了直角三角形的又一个特征. 如果直角三角形的两直角边分别为a,
b ,斜边为c,那么即直角三角形两直角边的平方和等于斜边的平方。作业:
习题18.1第1、2、3题。 再见!
观察图(2):正方形A、B、C的面积各是多少?
你能得到什么推断?
结论1 以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的大正方形的面积.根据图形所示填表:探究活动二分析表中数据,你发现了什么? 结论2 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的大正方形的面积.练习:
(1)、求下列图中字母所表示的正方形
的面积 (2)你能发现直角三角形三边长度之间
存在什么关系吗? (3)分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度. (2)中的规律对这个三角形仍然成立吗?动手实践 直角三角形两直角边的平方和等于斜边的平方. 如果直角三角形两直角边分别为a,b,斜边为c,那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方. 勾股定理a2 + b2 =c2
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦,“勾股定理”因此而得名. (在西方称为毕达哥拉斯定理)数学小史中国古代数学家——赵爽的验证方法 还可以认为是四个直角三角形与一个小正方形面积的和,即∴2002年在北京召开的国际数学家大会的会标就是依据我国古代数学家赵爽的弦图制作的。∴ ∵正方形ABCD的面积为c2例. 一架高为10米的木梯,架在高为8米的墙上(如图),这时梯脚与墙的距离是多少米? ABC解:∵在直角?ABC中,∠C=90°
∴ 根据勾股定理得
BC2 + AC2 = AB2
又∵AC=8 米 AB=10米
∴BC= AB2—AC2
= 102 — 82
= 6 米基础巩固练习:
1.填空: (1)直角?ABC的两条直角边a=3, b=4,则斜边c = 。 (2). 一个三角形的三个内角之比为1:2:3,则此三角形是___,若这三个角所对的边分别为a,b,c,则它们的关系是____. 2.求出下列直角三角形中未知边的长度收获的喜悦 勾股定理从边的角度刻画了直角三角形的又一个特征. 如果直角三角形的两直角边分别为a,
b ,斜边为c,那么即直角三角形两直角边的平方和等于斜边的平方。作业:
习题18.1第1、2、3题。 再见!
