角的复习

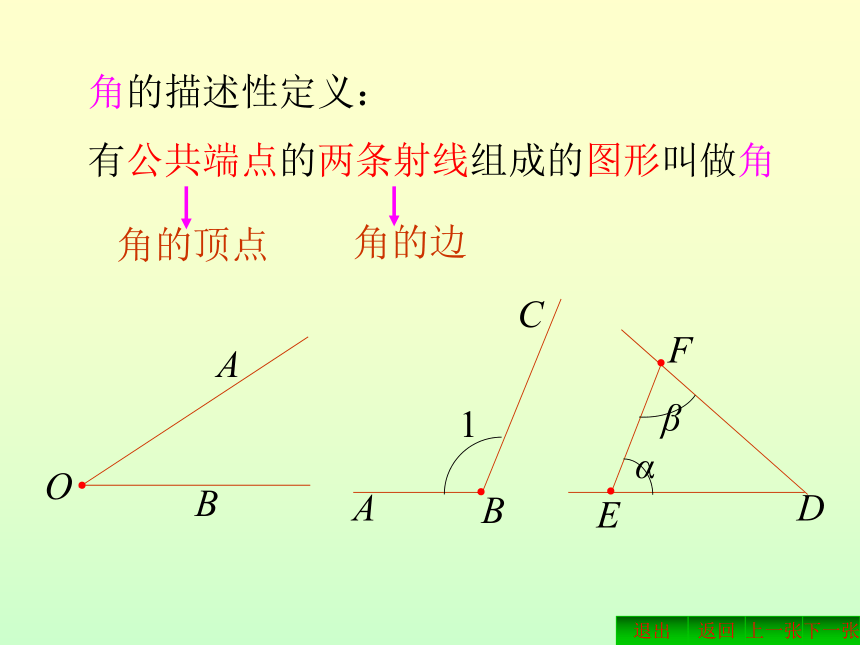
课件24张PPT。角复习返回下一张上一张退出角的描述性定义：
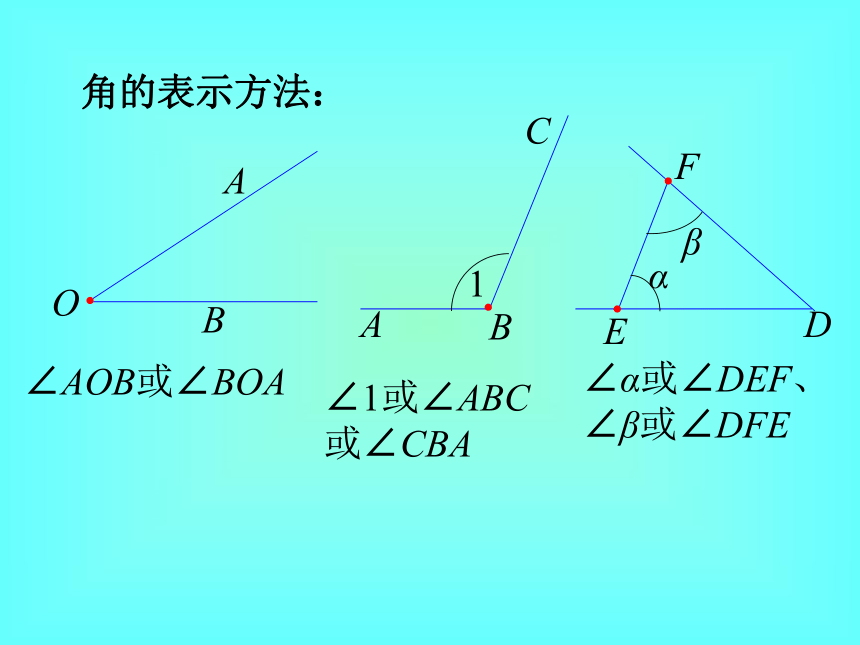
有公共端点的两条射线组成的图形叫做角角的顶点角的边OABABCFED1αβ●●●●角的表示方法：OABABCFED1αβ∠AOB或∠BOA∠1或∠ABC或∠CBA∠α或∠DEF、∠β或∠DFE●●●●角的平分线从一个角的顶点引一条
射线，如果把这个角分
成两个相等的角，那么
这条射线叫做这个角的
平分线
反 之 ，也 成 立∵OB是∠AOC的角平分线
∴ ∠AOB= ∠BOC= ∠AOC
或∠AOC= 2∠AOB= 2∠BOC
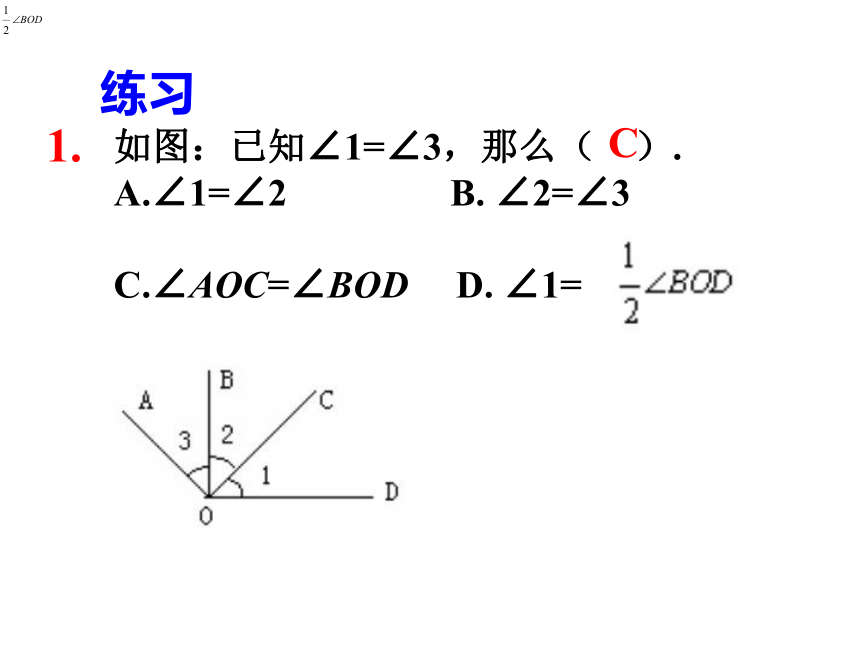
A BCO练习如图：已知∠1=∠3，那么（ ）.
A.∠1=∠2 B. ∠2=∠3

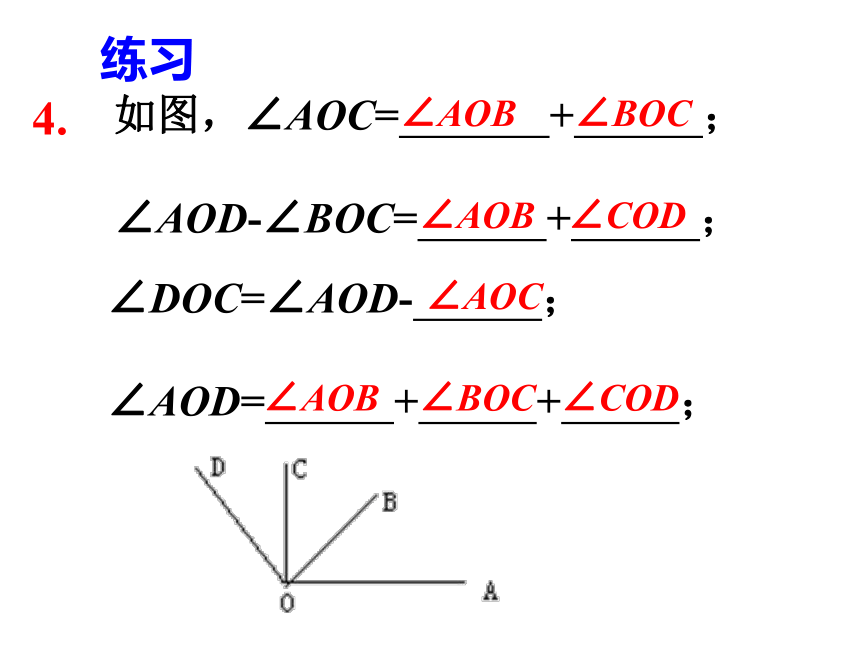
C.∠AOC=∠BOD D. ∠1=C1.练习4.如图，∠AOC= + ；
∠AOD-∠BOC= + ；∠DOC=∠AOD- ；
∠AOD= + + ；∠AOB∠BOC∠COD∠AOB∠AOC∠AOB∠BOC∠COD6. 用一副三角尺拼出下面度数的角。75° 105 ° 120° 135° 150° 180° P40 6、 一、角的度量单位角的度量单位是度、分、秒，是六十进制1°的60分之一为1分，记作“1′”，即1°＝60′1′的60分之一为1秒，记作“1″”，即1′＝60″1个周角的360分之一是1度的角，记作“1°”例 计算：
把18°25′12 ″化成用度表示的角.解：所以18°25′ 12″ =___________°.先把12″ 化成分，即12″ =（12? ）=0.2′再把（25+0.2）′化成度，即
（25+0.2）′=（25.2? ）°=0.42°，18.42°尝试练习四、余角和补角的性质1.余角和补角的定义如果两个角的和是90°，那么这两个角互为余角，简称“互余”.如果两个角的和是180°，那么这两个角互为补角，简称“互补”在图1、图2、图3中找出互余的角
和互补的角.1.余角和补角的性质同角或等角的余角相等同角或等角的补角相等已知，如图
∠AOC= ∠ BOD
= ∠COE=90 °，
找出（1）互余的角；
（2）互补的角；
（3）相等的角.
（直角均除外）（1） ∠1与∠3， ∠1与∠4， ∠1与∠3， ∠1与∠4；
（2） ∠1、 ∠2与∠AOD， ∠3、 ∠4与∠BOE；
（3） ∠1=∠2， ∠3= ∠4小组讨论：实验与探究一在两条直线相交所得的四个角中，每两个角在顶点、边上各有什么特点？O试一试BOA动动脑、动动手：
你能画出∠AOB的对顶角吗？))交流与发现ADClmOB概念1. 垂直２.垂线３.垂足表示法ＡＢ⊥ＣＤ　m⊥l垂直的定义与表示法是什么?当两条直线互相垂直时,所成的四个角都是直角吗?为什么?∠BOC=90° 在两条直线相交所成的四个角中,如果有一个角是直角,就说这两条直线互相垂直其中一条直线叫做另一条直线的垂线, 它们的交点叫做垂足返回例：如图直线AB与直线CD相交于点O，OE⊥AB.
已知∠BOD=45°，求∠COE的度数.解：∵OE⊥AB（已知）
∴∠AOE=90°（垂直定义）
∵∠AOC=∠BOD=45°（对顶角相等）
∴∠COE = ∠AOC+ ∠AOE
=45°+90°
= 135°
如何画一条线段或一条射线的垂线？画已知线段、射线的垂线其实就是经过已知点作已知线段、射线所在的直线的垂线.返回拓展返回通过上述方法画出的垂线有几条？ 从中你能发现什么结论？ 交流3.如图，分别过点B、C，画AD所在直线的垂线，垂足分别为M、NABCDMN返回如图，在灌溉时需要把河AB中的水引到C处，如何挖渠能使渠道最短？ ABCD探索与发现线段CD叫做点C到直线AB的垂线段我发现线段AD的长度叫做点A到直线l的距离