18.1勾股定理1课件
图片预览




文档简介
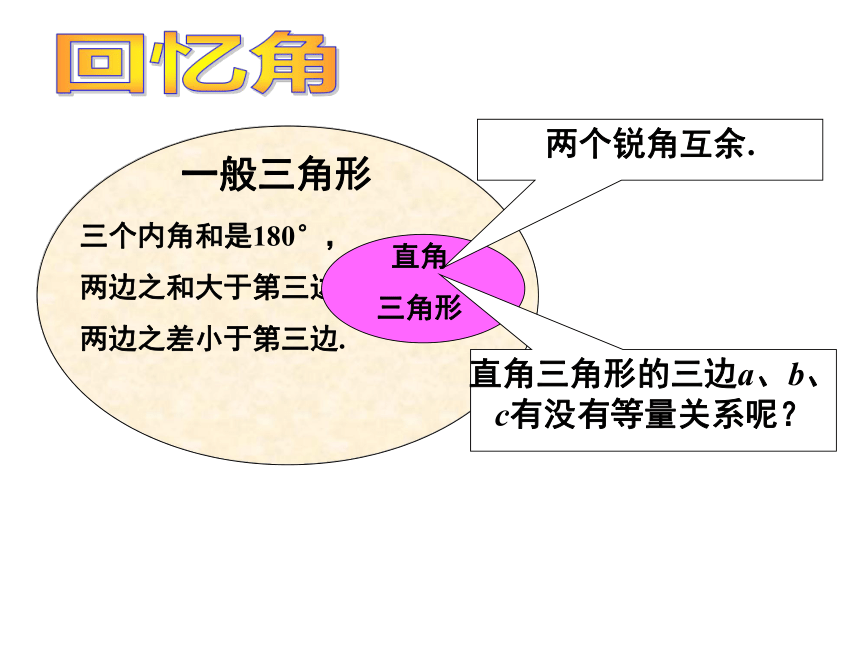
课件44张PPT。18.1 勾股定理(1)著名数学家华罗庚曾建议用这个图作为与“外星人”联系的信号.你知道这是为什么吗?你见过这个漂亮的图案吗?这个图案有什么意义?回忆角一般三角形三个内角和是180°,
两边之和大于第三边,
两边之差小于第三边.直角
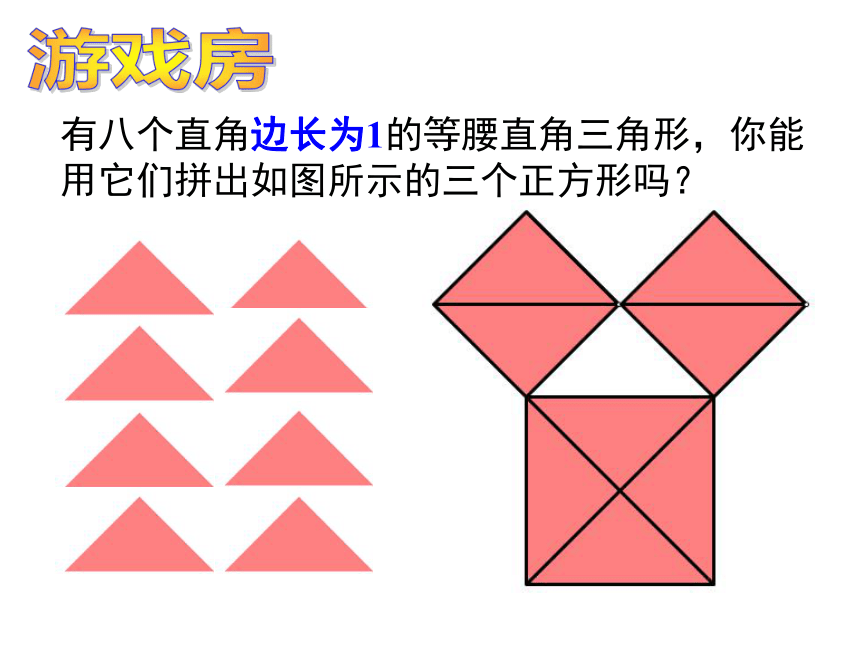
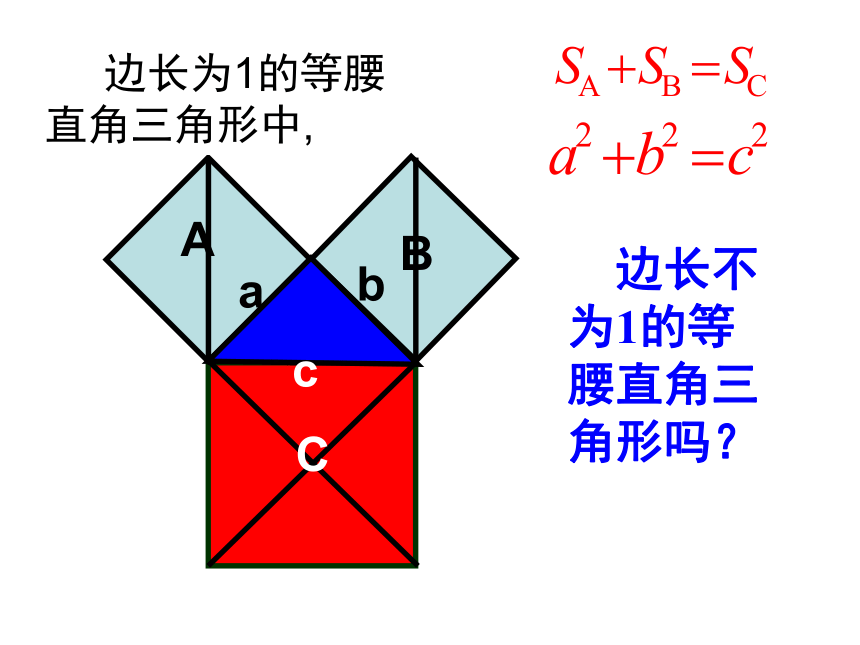
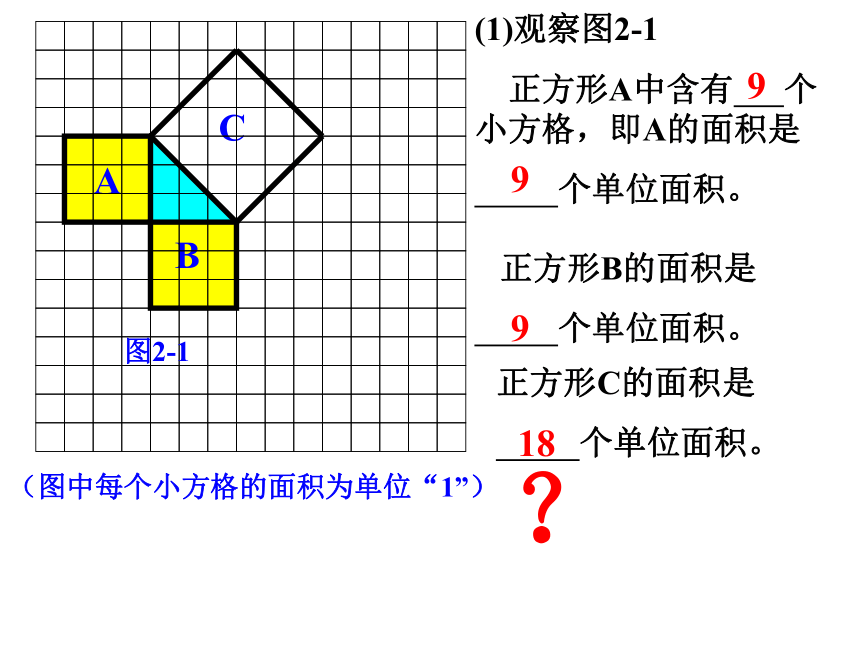
三角形两个锐角互余.直角三角形的三边a、b、c有没有等量关系呢?有八个直角边长为1的等腰直角三角形,你能用它们拼出如图所示的三个正方形吗? 游戏房 边长为1的等腰直角三角形中, 边长不为1的等腰直角三角形吗?CBAbcaABC(图中每个小方格的面积为单位“1”)图2-1(1)观察图2-1
正方形A中含有 个小方格,即A的面积是
个单位面积。 正方形B的面积是
个单位面积。正方形C的面积是
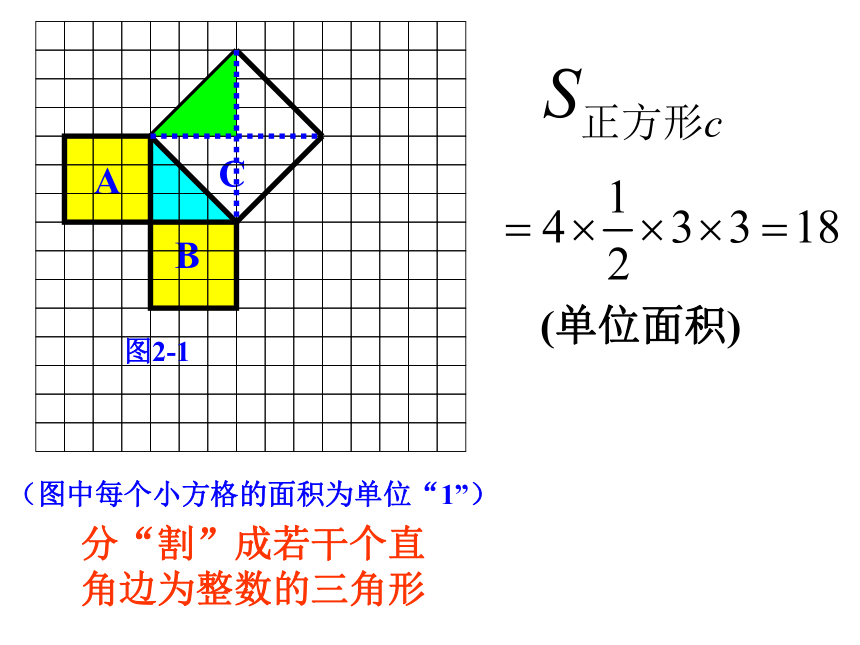
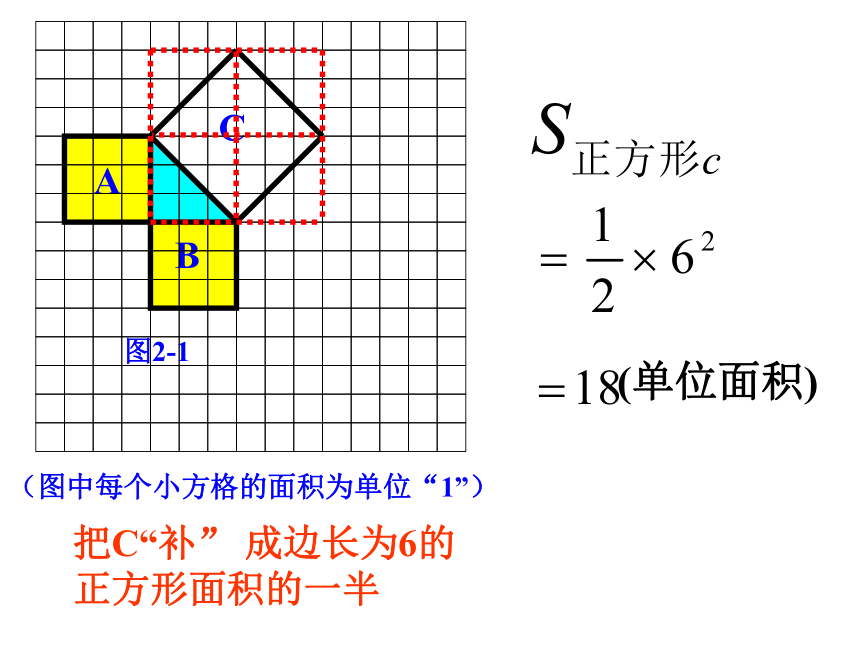
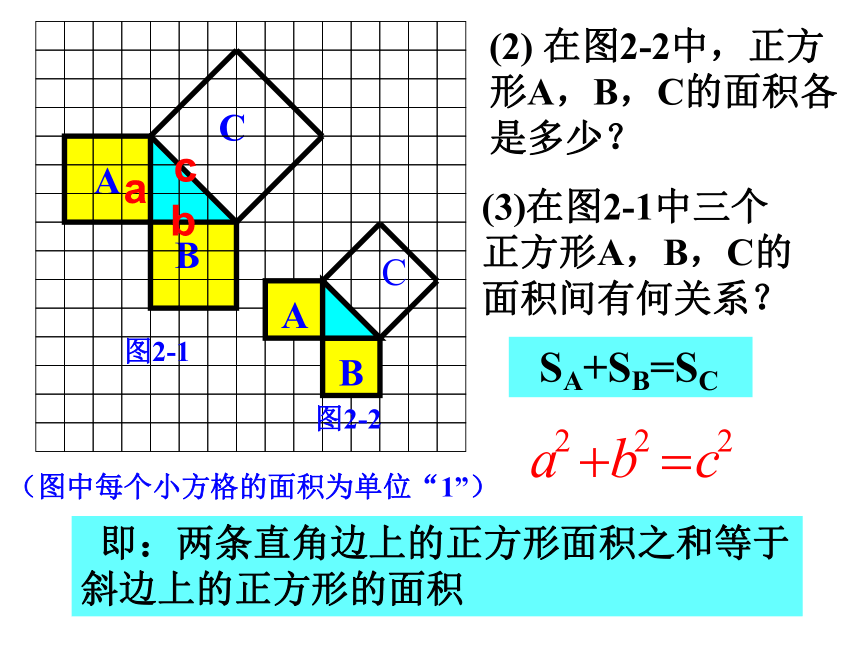
个单位面积。99918?AB C图2-1分“割”成若干个直角边为整数的三角形(单位面积)(图中每个小方格的面积为单位“1”)ABC图2-1(单位面积)把C“补” 成边长为6的正方形面积的一半(图中每个小方格的面积为单位“1”)ABC图2-1图2-2(2) 在图2-2中,正方形A,B,C的面积各是多少?(3)在图2-1中三个正方形A,B,C的面积间有何关系? SA+SB=SC 即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积bca(图中每个小方格的面积为单位“1”) 在等腰直角三角形中, 在一般的直角三角形中呢?CBAbca(1)观察右边两幅图: (2)填表(每个小正方形的面积为单位1):416 ??探究园(3) 怎样求正方形C的面积呢?99734SC = S大正方形 - 4×S小直角三角形 探究园“补”的方法15补 16割 17拼(3) 怎样求正方形C的面积呢?“割”的方法34SC = 4×S小直角三角形 + S小正方形探究园15补 16割 17拼“拼”的方法你知道是怎样拼的吗?Sc= 16+9=25探究园15补 16割 17拼“平移”“旋转”的方法(1) 观察右边两幅图: (2)填表(每个小正方形的面积为单位1):416 探究园 9 91325根据表中数据,你得到了什么? (1) 你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗? (2) 你能发现直角三角形三边长度之间存在什么关系吗?探究园画Rt⊿,
取直角边长为
3、4格(示范)
6、8格(生1)
9、12格(生2)
5、12格(生3)“量”的方法任意取两直角边长(生4)
再测量斜边长验证定理.探究园┏a2+b2=c2acb 命题1 如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.如何证明此命题呢?猜想归纳勾股弦探究园 我国对勾股定理的证明采取的是割补法,最早的形式见于公元三、四世纪赵爽的《勾股圆方图注》在这篇短文中,赵爽画了一张他所谓的“弦图”,其中
每一个直角三角形称为
“朱实”,中间的一个
正方形称为“黄实”,
以弦为边的大正方形叫
“弦实”,所以,如果
以a、b、c 分别表示勾、股、弦之长.如何证明?知识窗赵爽给出的勾股定理的证明cabc2ba= a2+b2ba探究园Ca+bcba赵爽给出的勾股定理的证明下 勾股定理探究园如果直角三角形两直角边长分别为a、b,斜边长为c,那么勾 股 定 理 命题1 即 直角三角形两直角边的平方和等于
斜边的平方.应用:Rt△ABC中, ∠C=90°, 则 满足a2 +b2=c2的三个正整数,称为勾股数。下会徽 “赵爽弦图”表现了我国古代数学家对数学的钻研精神, 它是我国古代数学的骄傲. 因此这个图案被选为2002年在北京召开的国际数学家大会的会徽.知
识
窗下 其他传说中毕达哥拉斯证法知识窗美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 人们为了纪念他对勾股定理直观、简捷、易懂、明了的 证明,就把这一证法称为“总统”证法.有趣的总统证法知识窗例1.求出下列直角三角形中的x.5x13解:(1)在Rt△ABC中,由勾股定理得:AB2=AC2+BC2X2 =36+64x2 =100x2=62+82∴ x=10 ∵x>0 x2+52=132 x2=132-52x2=144∴ x=12(2)在Rt△ABC中,由勾股定理:AB2+AC2=BC2∵x>0ACBACB勾股数方程 练习例练厅P625400P的面积 =____225BACAB =_____AC =_____BC =_____251520演练台1.2.求下列图中表示边的未知数x、y、z的值.①81144xyz②③x = 25y = 5z = 7x2 =144+81
= 225y2 =169-144
= 25z2 = 625-576
= 49比一比看看谁算得快!3.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x结294. 在⊿ABC中, ∠C=900,(1) 若a=8, b=6, 则 c=____,(2) 若c=20, b=12, 则 a=___,(3) 若c=13, a=5, 则 b=____,1016127. 在Rt⊿ABC中, 若a=3, b=4, 则
c=________.55. 在Rt△ABC中,∠C=900,a=2, c=5, 则b=___.6. 在Rt△ABC中, ∠B=900,a=3, b=4, 则c=___.1.成立条件: 在直角三角形中;3.作用:已知直角三角形任意两边长,
求第三边长.2.公式变形:如果直角三角形两直角边长分别为a、b,斜边长为c,那么勾 股 定 理(注意:哪条边是斜边)即 直角三角形两直角边的平方和等于斜边的平方.作 36815A49B258.求下列图中字母所代表的正方形的面积:演练台结论:S1+S2+S3+S4=S5+S6=S7演练台解: ∵ SE= 49S1=SA+SBS2=SC+SD∴ SA+SB+SC+S
= S1+S2
= SE
= 49求 SA+SB+SC+SD=? 演练台美丽的勾股树(一)美丽的勾股树(二)美丽的勾股树(三)作业快餐必做题:1. P70第1,2,3
选做题:P71 第11、12题.2. 查阅、收集与勾股定理有关的知识, 证明方法和应用等, 然后小组交流、展示. 一个门框的尺寸如图所示,一块长 3m,宽2.2m的薄板能否从门框内通过?为什么?探究1 如图一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子低端B也外移0.5m 吗?ACDBO探究2
两边之和大于第三边,
两边之差小于第三边.直角
三角形两个锐角互余.直角三角形的三边a、b、c有没有等量关系呢?有八个直角边长为1的等腰直角三角形,你能用它们拼出如图所示的三个正方形吗? 游戏房 边长为1的等腰直角三角形中, 边长不为1的等腰直角三角形吗?CBAbcaABC(图中每个小方格的面积为单位“1”)图2-1(1)观察图2-1
正方形A中含有 个小方格,即A的面积是
个单位面积。 正方形B的面积是
个单位面积。正方形C的面积是
个单位面积。99918?AB C图2-1分“割”成若干个直角边为整数的三角形(单位面积)(图中每个小方格的面积为单位“1”)ABC图2-1(单位面积)把C“补” 成边长为6的正方形面积的一半(图中每个小方格的面积为单位“1”)ABC图2-1图2-2(2) 在图2-2中,正方形A,B,C的面积各是多少?(3)在图2-1中三个正方形A,B,C的面积间有何关系? SA+SB=SC 即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积bca(图中每个小方格的面积为单位“1”) 在等腰直角三角形中, 在一般的直角三角形中呢?CBAbca(1)观察右边两幅图: (2)填表(每个小正方形的面积为单位1):416 ??探究园(3) 怎样求正方形C的面积呢?99734SC = S大正方形 - 4×S小直角三角形 探究园“补”的方法15补 16割 17拼(3) 怎样求正方形C的面积呢?“割”的方法34SC = 4×S小直角三角形 + S小正方形探究园15补 16割 17拼“拼”的方法你知道是怎样拼的吗?Sc= 16+9=25探究园15补 16割 17拼“平移”“旋转”的方法(1) 观察右边两幅图: (2)填表(每个小正方形的面积为单位1):416 探究园 9 91325根据表中数据,你得到了什么? (1) 你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗? (2) 你能发现直角三角形三边长度之间存在什么关系吗?探究园画Rt⊿,
取直角边长为
3、4格(示范)
6、8格(生1)
9、12格(生2)
5、12格(生3)“量”的方法任意取两直角边长(生4)
再测量斜边长验证定理.探究园┏a2+b2=c2acb 命题1 如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.如何证明此命题呢?猜想归纳勾股弦探究园 我国对勾股定理的证明采取的是割补法,最早的形式见于公元三、四世纪赵爽的《勾股圆方图注》在这篇短文中,赵爽画了一张他所谓的“弦图”,其中
每一个直角三角形称为
“朱实”,中间的一个
正方形称为“黄实”,
以弦为边的大正方形叫
“弦实”,所以,如果
以a、b、c 分别表示勾、股、弦之长.如何证明?知识窗赵爽给出的勾股定理的证明cabc2ba= a2+b2ba探究园Ca+bcba赵爽给出的勾股定理的证明下 勾股定理探究园如果直角三角形两直角边长分别为a、b,斜边长为c,那么勾 股 定 理 命题1 即 直角三角形两直角边的平方和等于
斜边的平方.应用:Rt△ABC中, ∠C=90°, 则 满足a2 +b2=c2的三个正整数,称为勾股数。下会徽 “赵爽弦图”表现了我国古代数学家对数学的钻研精神, 它是我国古代数学的骄傲. 因此这个图案被选为2002年在北京召开的国际数学家大会的会徽.知
识
窗下 其他传说中毕达哥拉斯证法知识窗美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 人们为了纪念他对勾股定理直观、简捷、易懂、明了的 证明,就把这一证法称为“总统”证法.有趣的总统证法知识窗例1.求出下列直角三角形中的x.5x13解:(1)在Rt△ABC中,由勾股定理得:AB2=AC2+BC2X2 =36+64x2 =100x2=62+82∴ x=10 ∵x>0 x2+52=132 x2=132-52x2=144∴ x=12(2)在Rt△ABC中,由勾股定理:AB2+AC2=BC2∵x>0ACBACB勾股数方程 练习例练厅P625400P的面积 =____225BACAB =_____AC =_____BC =_____251520演练台1.2.求下列图中表示边的未知数x、y、z的值.①81144xyz②③x = 25y = 5z = 7x2 =144+81
= 225y2 =169-144
= 25z2 = 625-576
= 49比一比看看谁算得快!3.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x结294. 在⊿ABC中, ∠C=900,(1) 若a=8, b=6, 则 c=____,(2) 若c=20, b=12, 则 a=___,(3) 若c=13, a=5, 则 b=____,1016127. 在Rt⊿ABC中, 若a=3, b=4, 则
c=________.55. 在Rt△ABC中,∠C=900,a=2, c=5, 则b=___.6. 在Rt△ABC中, ∠B=900,a=3, b=4, 则c=___.1.成立条件: 在直角三角形中;3.作用:已知直角三角形任意两边长,
求第三边长.2.公式变形:如果直角三角形两直角边长分别为a、b,斜边长为c,那么勾 股 定 理(注意:哪条边是斜边)即 直角三角形两直角边的平方和等于斜边的平方.作 36815A49B258.求下列图中字母所代表的正方形的面积:演练台结论:S1+S2+S3+S4=S5+S6=S7演练台解: ∵ SE= 49S1=SA+SBS2=SC+SD∴ SA+SB+SC+S
= S1+S2
= SE
= 49求 SA+SB+SC+SD=? 演练台美丽的勾股树(一)美丽的勾股树(二)美丽的勾股树(三)作业快餐必做题:1. P70第1,2,3
选做题:P71 第11、12题.2. 查阅、收集与勾股定理有关的知识, 证明方法和应用等, 然后小组交流、展示. 一个门框的尺寸如图所示,一块长 3m,宽2.2m的薄板能否从门框内通过?为什么?探究1 如图一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子低端B也外移0.5m 吗?ACDBO探究2
