华师大版数学九年级下册同步课件:26.3 第2课时 二次函数与一元二次方程及一元二次不等式的关系(共20张PPT)
文档属性
| 名称 | 华师大版数学九年级下册同步课件:26.3 第2课时 二次函数与一元二次方程及一元二次不等式的关系(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 513.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 08:54:30 | ||
图片预览






文档简介
(共20张PPT)
26.3 第2课时
二次函数与一元二次方程及一元二次不等式的关系
第26章 二次函数
复习导入
1.求一次函数y=2x-4的图象与x轴交点的坐标.
x=2
2.一次函数与一元一次方程、一元一次不等式之间的关系是什么
一次函数每一个确定函数值就对应一个一元一次方程,一次函数值的确定区间对应一个一元一次不等式(组)
函数值y=0时x的值,即函数图象与x轴交点的横坐标。
3.下列方程与函数形式上有何联系
x2-2x-3=0,y=x2-2x-3
方程左边的式子就是函数表达式
4.方程的根是函数的什么值
你已具备学习新知的能力,让我们开始今天的学习!
获取新知
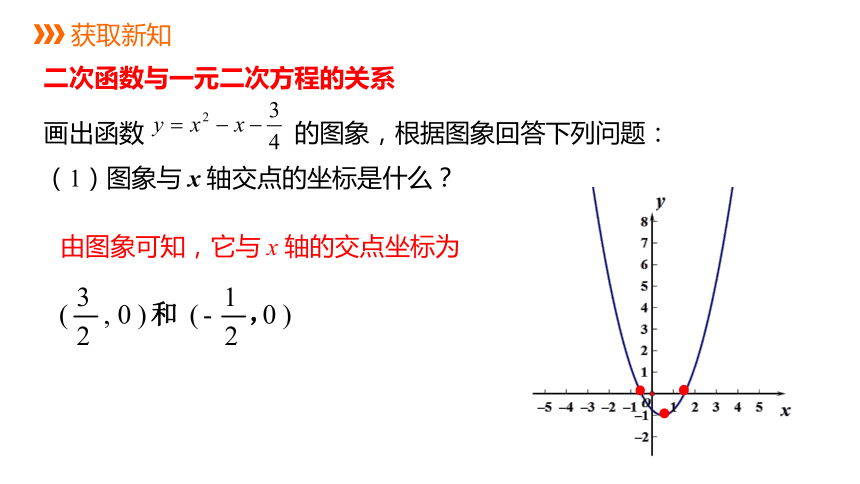
画出函数 的图象,根据图象回答下列问题:
(1)图象与 x 轴交点的坐标是什么?
由图象可知,它与 x 轴的交点坐标为
二次函数与一元二次方程的关系
(2)当x取何值时y=0 ?这里x的取值与方程有什么关系?
由(1)可知:当 时,y=0;解这个一元二次方程可知:这里的x的值是一元二次方程的两个根.
二次函数与x轴交点的横坐标即为对应的一元二次方程的解。
(3)你能从中得到什么启发?
2.二次函数y=ax2+bx+c的图象与轴的交点情况有三种:
有两个交点,有一个交点,没有交点.
如果抛物线y=ax2+bx+c与x轴交于两点(x1,0) (x2,0)则x1,x2是一元二 次方程ax2+bx+c=0的两个不等实根,反之亦成立.
二次函数与一元二次方程是紧密联系又相互渗透的,两者经常综合命题
1.二次函数y=ax2+bx+c,当y=0(或其他数值m)时,就变成了一元二次方程ax2+bx+c=0(或m).
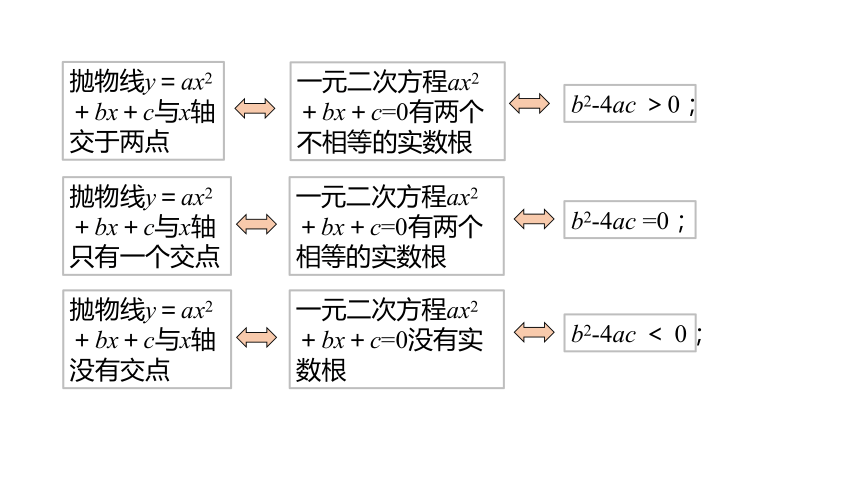
抛物线y=ax2+bx+c与x轴交于两点
一元二次方程ax2+bx+c=0有两个不相等的实数根
b2-4ac >0;
抛物线y=ax2+bx+c与x轴只有一个交点
一元二次方程ax2+bx+c=0有两个相等的实数根
b2-4ac =0;
抛物线y=ax2+bx+c与x轴没有交点
一元二次方程ax2+bx+c=0没有实数根
b2-4ac < 0;
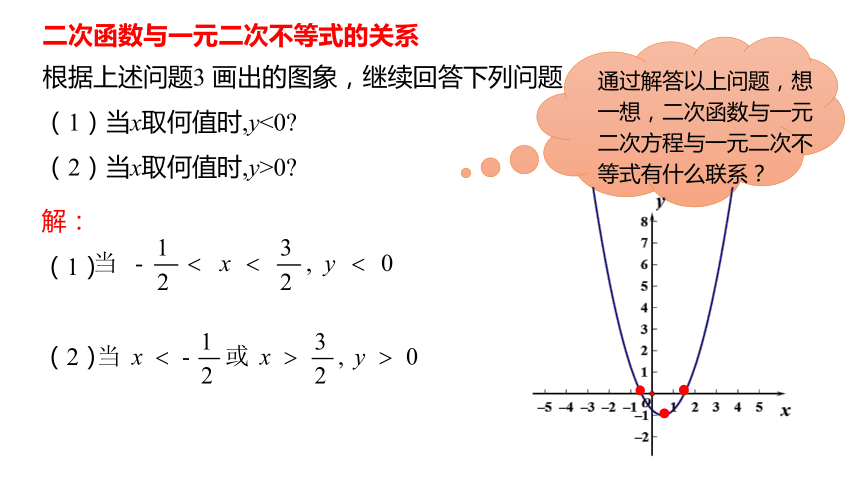
根据上述问题3 画出的图象,继续回答下列问题:
(1)当x取何值时,y<0
(2)当x取何值时,y>0
通过解答以上问题,想一想,二次函数与一元二次方程与一元二次不等式有什么联系?
解:
(1)
(2)
二次函数与一元二次不等式的关系
问题4
育才中学九年级(3)班的学生在上节课的练习中出 现了争论:解方程
时,几乎所有学生都是将方程化为 画出函数 的图象,观察它与x轴的交点,得出方程的根.唯独小刘没有将方程移项,而是分别画出了函数 y=x2和
y = 的图象,如图,认为它们的交点
A、B的横坐标 和2就是原方程的根.
你认为小刘的解法对吗?
运用小刘的方法求下列方程的根,并检验小刘的方法是否合理。
(1)x2+x-1=0(精确到0.1)
由图象可知:
方程的根为x1≈0.6,x2≈-1.6
(2)2x2-3x-2=0
由图象可知:
方程的根为x1=2,x2=
例1 求抛物线 y=3x2-8x+4与x轴的两个公共点的坐标.
例题讲解
令y=0,则3x2-8x+4=0,
解方程得:x1= x2=2.
∴抛物线y=3x2-8x+4与x轴的两个公共点的坐标
为 (2,0).
解:
例2:求一元二次方程 的根的近似值(精确到0.1).
分析:一元二次方程 x -2x-1=0 的根就是抛物线 y=x -2x-1 与x轴的交点的横坐标,因此我们可以先画出这条抛物线,然后从图上找出它与x轴的交点的横坐标,这种解一元二次方程的方法叫作图象法.
解:画出函数 y=x -2x-1 的图象(如下图),由图象可知,方程有两个实数根,一个在-1与0之间,另一个在2与3之间.
先求位于-1到0之间的根,由图象可估计这个根是-0.4或-0.5,利用计算器进行探索,见下表:
x … -0.4 -0.5 …
y … -0.04 0.25 …
观察上表可以发现,当x分别取-0.4和-0.5时,对应的y由负变正,可见在-0.5与-0.4之间肯定有一个x使y=0,即有y=x2-2x-1的一个根,题目只要求精确到0.1,这时取x=-0.4或x=-0.5都符合要求.但当x=-0.4时更为接近0.故x1≈-0.4.同理可得另一近似值为x2≈2.4.
一元二次方程的图象解法
利用二次函数的图象求一元二次方程ax2+bx+c=0的近似根.
(1)用描点法作二次函数 y= ax2+bx+c的图象;
(2)观察估计二次函数 y= ax2+bx+c的图象与x轴的交点的横坐标;
(3)确定方程ax2+bx+c=0的解;
1.抛物线y=-x 2 +4x-4与坐标轴的交点个数为( )
A.0 B.1 C.2 D.3
随堂演练
C
2.二次函数y=x2-2x-3的图象如图所示,则当函数值y<0时, x的取值范围是( )
A.x<-1 B.x>3
C.-13
C
3.在平面直角坐标系中,二次函数y1=-x2+4x和一次函数y2=2x的图象如图所示,那么不等式-x2+4x>2x的解集是 ( )
A.x<0 B.0C.0C
4.已知二次函数y=2x2-2和一次函数y=5x+1.
(1)你能用图象法求出方程2x2-2=5x+1的解吗 试试看;
(2)请通过解方程的方法验证(1)中的答案.
解:(1)如图,在平面直角坐标系内画出函数y=2x2-2和函数y=5x+1的图象,
两图象交点的横坐标是- ,3,
∴方程2x2-2=5x+1的解是x1=-,x2=3.
(2)整理得2x2-5x-3=0,
因式分解,得(2x+1)(x-3)=0.
解得x1=- ,x2=3.
课堂小结
判别式△=b2-4ac
二次函数y=ax2+bx+c (a>0) 的图象
一元二次方程ax2+bx+c=0 (a≠0)的根
不等式ax2+bx+c>0(a>0)的解集
不等式ax2+bx+c<0(a>0)的解集
x2
x1
x
y
O
O
x1= x2
x
y
x
O
y
△>0
△=0
△<0
x1 ; x2
x1 =x2
=-b/2a
没有实数根
xx2
x ≠ x1的一切实数
所有实数
x1无解
无解
26.3 第2课时
二次函数与一元二次方程及一元二次不等式的关系
第26章 二次函数
复习导入
1.求一次函数y=2x-4的图象与x轴交点的坐标.
x=2
2.一次函数与一元一次方程、一元一次不等式之间的关系是什么
一次函数每一个确定函数值就对应一个一元一次方程,一次函数值的确定区间对应一个一元一次不等式(组)
函数值y=0时x的值,即函数图象与x轴交点的横坐标。
3.下列方程与函数形式上有何联系
x2-2x-3=0,y=x2-2x-3
方程左边的式子就是函数表达式
4.方程的根是函数的什么值
你已具备学习新知的能力,让我们开始今天的学习!
获取新知
画出函数 的图象,根据图象回答下列问题:
(1)图象与 x 轴交点的坐标是什么?
由图象可知,它与 x 轴的交点坐标为
二次函数与一元二次方程的关系
(2)当x取何值时y=0 ?这里x的取值与方程有什么关系?
由(1)可知:当 时,y=0;解这个一元二次方程可知:这里的x的值是一元二次方程的两个根.
二次函数与x轴交点的横坐标即为对应的一元二次方程的解。
(3)你能从中得到什么启发?
2.二次函数y=ax2+bx+c的图象与轴的交点情况有三种:
有两个交点,有一个交点,没有交点.
如果抛物线y=ax2+bx+c与x轴交于两点(x1,0) (x2,0)则x1,x2是一元二 次方程ax2+bx+c=0的两个不等实根,反之亦成立.
二次函数与一元二次方程是紧密联系又相互渗透的,两者经常综合命题
1.二次函数y=ax2+bx+c,当y=0(或其他数值m)时,就变成了一元二次方程ax2+bx+c=0(或m).
抛物线y=ax2+bx+c与x轴交于两点
一元二次方程ax2+bx+c=0有两个不相等的实数根
b2-4ac >0;
抛物线y=ax2+bx+c与x轴只有一个交点
一元二次方程ax2+bx+c=0有两个相等的实数根
b2-4ac =0;
抛物线y=ax2+bx+c与x轴没有交点
一元二次方程ax2+bx+c=0没有实数根
b2-4ac < 0;
根据上述问题3 画出的图象,继续回答下列问题:
(1)当x取何值时,y<0
(2)当x取何值时,y>0
通过解答以上问题,想一想,二次函数与一元二次方程与一元二次不等式有什么联系?
解:
(1)
(2)
二次函数与一元二次不等式的关系
问题4
育才中学九年级(3)班的学生在上节课的练习中出 现了争论:解方程
时,几乎所有学生都是将方程化为 画出函数 的图象,观察它与x轴的交点,得出方程的根.唯独小刘没有将方程移项,而是分别画出了函数 y=x2和
y = 的图象,如图,认为它们的交点
A、B的横坐标 和2就是原方程的根.
你认为小刘的解法对吗?
运用小刘的方法求下列方程的根,并检验小刘的方法是否合理。
(1)x2+x-1=0(精确到0.1)
由图象可知:
方程的根为x1≈0.6,x2≈-1.6
(2)2x2-3x-2=0
由图象可知:
方程的根为x1=2,x2=
例1 求抛物线 y=3x2-8x+4与x轴的两个公共点的坐标.
例题讲解
令y=0,则3x2-8x+4=0,
解方程得:x1= x2=2.
∴抛物线y=3x2-8x+4与x轴的两个公共点的坐标
为 (2,0).
解:
例2:求一元二次方程 的根的近似值(精确到0.1).
分析:一元二次方程 x -2x-1=0 的根就是抛物线 y=x -2x-1 与x轴的交点的横坐标,因此我们可以先画出这条抛物线,然后从图上找出它与x轴的交点的横坐标,这种解一元二次方程的方法叫作图象法.
解:画出函数 y=x -2x-1 的图象(如下图),由图象可知,方程有两个实数根,一个在-1与0之间,另一个在2与3之间.
先求位于-1到0之间的根,由图象可估计这个根是-0.4或-0.5,利用计算器进行探索,见下表:
x … -0.4 -0.5 …
y … -0.04 0.25 …
观察上表可以发现,当x分别取-0.4和-0.5时,对应的y由负变正,可见在-0.5与-0.4之间肯定有一个x使y=0,即有y=x2-2x-1的一个根,题目只要求精确到0.1,这时取x=-0.4或x=-0.5都符合要求.但当x=-0.4时更为接近0.故x1≈-0.4.同理可得另一近似值为x2≈2.4.
一元二次方程的图象解法
利用二次函数的图象求一元二次方程ax2+bx+c=0的近似根.
(1)用描点法作二次函数 y= ax2+bx+c的图象;
(2)观察估计二次函数 y= ax2+bx+c的图象与x轴的交点的横坐标;
(3)确定方程ax2+bx+c=0的解;
1.抛物线y=-x 2 +4x-4与坐标轴的交点个数为( )
A.0 B.1 C.2 D.3
随堂演练
C
2.二次函数y=x2-2x-3的图象如图所示,则当函数值y<0时, x的取值范围是( )
A.x<-1 B.x>3
C.-1
C
3.在平面直角坐标系中,二次函数y1=-x2+4x和一次函数y2=2x的图象如图所示,那么不等式-x2+4x>2x的解集是 ( )
A.x<0 B.0
4.已知二次函数y=2x2-2和一次函数y=5x+1.
(1)你能用图象法求出方程2x2-2=5x+1的解吗 试试看;
(2)请通过解方程的方法验证(1)中的答案.
解:(1)如图,在平面直角坐标系内画出函数y=2x2-2和函数y=5x+1的图象,
两图象交点的横坐标是- ,3,
∴方程2x2-2=5x+1的解是x1=-,x2=3.
(2)整理得2x2-5x-3=0,
因式分解,得(2x+1)(x-3)=0.
解得x1=- ,x2=3.
课堂小结
判别式△=b2-4ac
二次函数y=ax2+bx+c (a>0) 的图象
一元二次方程ax2+bx+c=0 (a≠0)的根
不等式ax2+bx+c>0(a>0)的解集
不等式ax2+bx+c<0(a>0)的解集
x2
x1
x
y
O
O
x1= x2
x
y
x
O
y
△>0
△=0
△<0
x1 ; x2
x1 =x2
=-b/2a
没有实数根
x
x ≠ x1的一切实数
所有实数
x1
无解
