华师大版数学九年级下册同步课件:27.2.1 点与圆的位置关系(共21张PPT)
文档属性
| 名称 | 华师大版数学九年级下册同步课件:27.2.1 点与圆的位置关系(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 09:13:06 | ||
图片预览




文档简介
(共21张PPT)
27.2.1 点与圆的位置关系
课堂小结
例题讲解
获取新知
随堂演练
情景导入
第27章 圆
情境导入
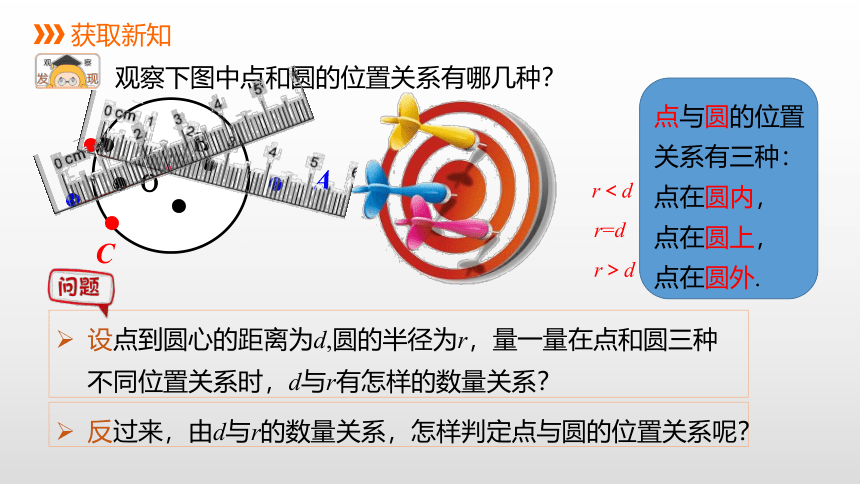
你玩过飞镖吗?它的靶子是由一些圆组成的,你知道击中靶子上不同位置的成绩是如何计算的吗?
.
o
.
C
.
.
.
. B
.
.A
.
点与圆的位置关系有三种:
点在圆内,
点在圆上,
点在圆外.
观察下图中点和圆的位置关系有哪几种?
设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?
反过来,由d与r的数量关系,怎样判定点与圆的位置关系呢?
r=d
r<d
r>d
获取新知
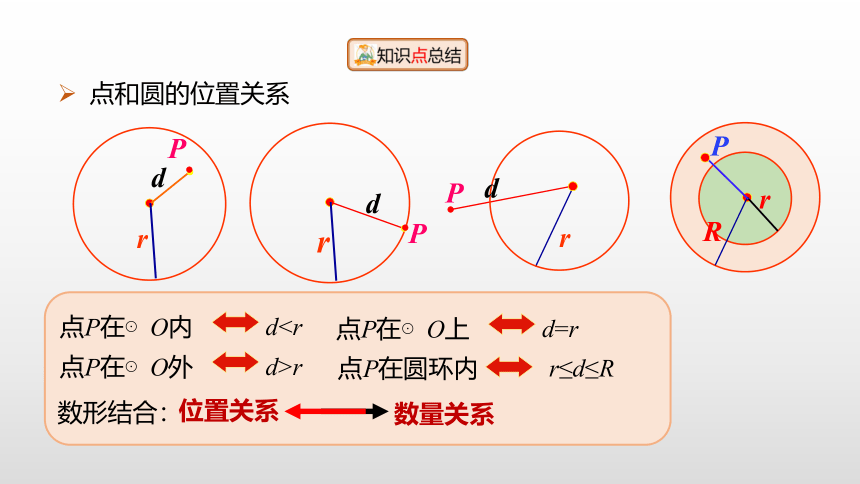
点和圆的位置关系
r
P
d
P
r
d
P
r
d
R
r
P
点P在⊙O内
d点P在⊙O上
d=r
点P在⊙O外
d>r
点P在圆环内
r≤d≤R
数形结合:
位置关系
数量关系
⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
圆内
圆上
圆外
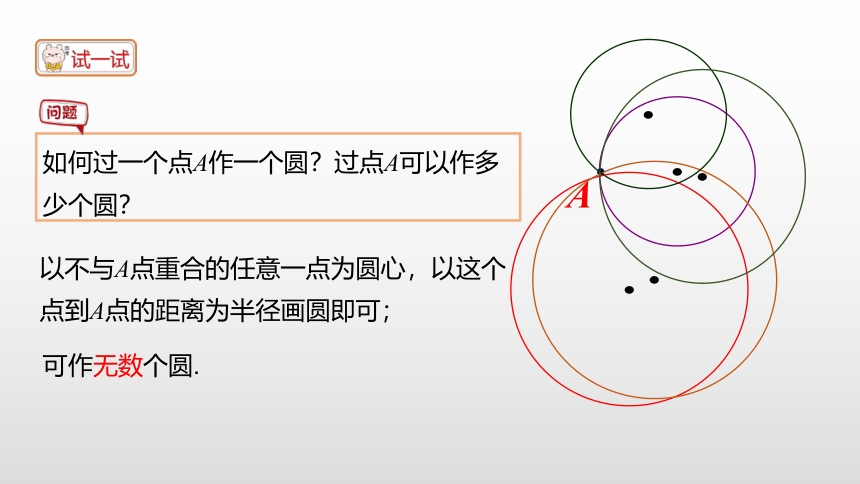
如何过一个点A作一个圆?过点A可以作多少个圆?
·
·
·
·
·
以不与A点重合的任意一点为圆心,以这个点到A点的距离为半径画圆即可;
A
可作无数个圆.
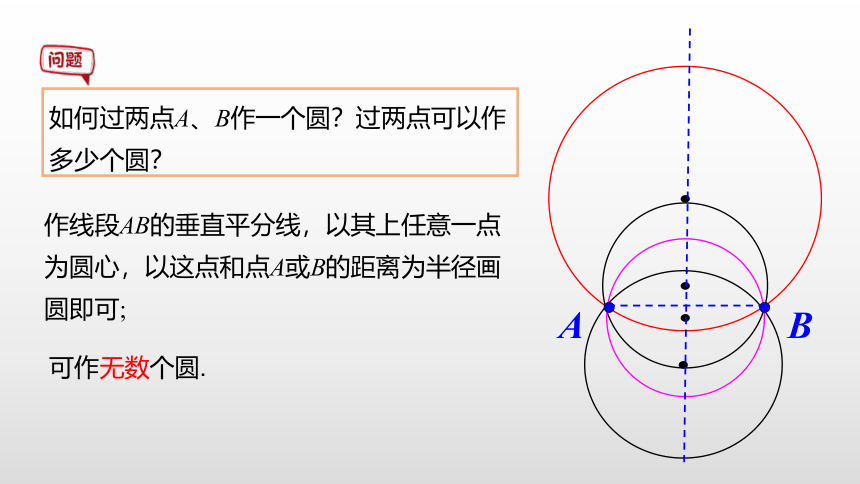
如何过两点A、B作一个圆?过两点可以作多少个圆?
·
·
·
·
A
B
作线段AB的垂直平分线,以其上任意一点为圆心,以这点和点A或B的距离为半径画圆即可;
可作无数个圆.
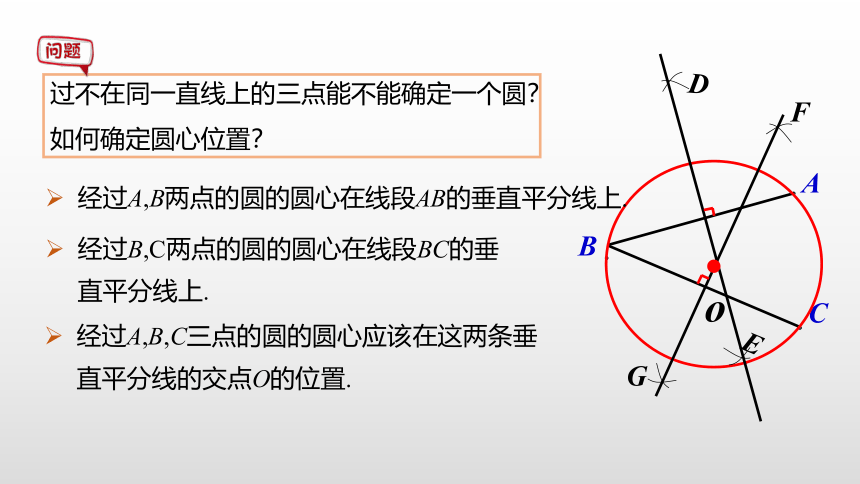
过不在同一直线上的三点能不能确定一个圆?
如何确定圆心位置?
A
B
C
D
E
G
F
●o
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
思考:如果A、B、C在同一条直线上,能画出经过这三点的圆吗?
l1
l2
A
B
C
P
如图,假设过同一条直线l上三点A、B、C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
有且只有
位置关系
定理:不在同一直线上的三个点确定一个圆.
已知:不在同一直线上的三点A、B、C.
求作: ⊙O,使它经过点A、B、C.
作法:
1、连结AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆。
所以⊙O就是所求作的圆.
O
N
M
F
E
A
B
C
已知△ABC,用直尺与圆规作出过A、B、C三点的圆.
A
B
C
O
三角形外接圆的作法:
(1)作三角形任意两边的垂直平分线,确定其交点;
(2)以该交点为圆心,以交点到三个顶点中任意一点的距离为半径作圆即可.
(1)任何一个三角形都有一个外接圆,而一个圆有无数个
内接三角形.一个三角形的外接圆是唯一的.
(2)锐角三角形的外心在三角形的内部;直角三角形的外
心在斜边中点处;钝角三角形的外心在三角形的外部.
(3)三角形的外心是三角形三条边的垂直平分线的交点,
它到三角形三个顶点的距离相等.
经过三角形三个顶点的圆就是这个三角形的外接圆,
三角形外接圆的圆心叫做这个三角形的外心.这个三角形叫做这个圆的内接三角形.
例题讲解
例1 如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以点A为圆心、3cm为半径画圆,并判断:
(1)点C与⊙A的位置关系;
(2)点B与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.
●
B
A
D
C
解:已知⊙A的半径r=3 cm.
(1) 因为 ,所以点C在⊙A上.
(2) 因为AB=5 cm>3 cm=r, 所以点B在⊙A外.
(3)因为 ,所以点D在⊙A内.
例2 如图,△ABC内接于⊙O,∠C=45°,AB=4,求⊙O 的半径.
解::如图,连接OA,OB,设⊙O的半径为r,
∵∠C=45°,∴∠AOB=2∠C=90°.
∴OA2+OB2=AB2,即r2+r2=42.
解得r1=2 ,r2=-2 (不符合题意,舍去).
∴⊙O的半径为2 .
还有其他的思路吗?
1.圆心为O的两个同心圆,半径分别为1和2,若OP= ,则点P在( )
A.大圆内 B.小圆内
C.小圆外 D.大圆内,小圆外
随堂演练
o
D
2.三角形的外心具有的性质是( )
A.到三边的距离相等. B.到三个顶点的距离相等.
C.外心在三角形的外. D.外心在三角形内.
3.等腰三角形底边上的高与一腰的垂直平分线的交点是( )
A.重心 B.垂心 C.外心 D.无法确定.
B
C
4.已知AB=4 cm,则过点A,B且半径为3 cm的圆有( )
A.1个 B.2个 C.3个 D.4个
B
5.如图,在△ABC中,点O在边AB上,且点O为△ABC的外心,求∠ACB的度数.
解:∵点O为△ABC的外心,
∴OA=OB=OC,
∴∠OAC=∠OCA,∠OCB=∠OBC.
∵∠OAC+∠OCA+∠OCB+∠OBC=180°,
∴∠OCA+∠OCB=90°,
即∠ACB=90°.
课堂小结
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d位置关系数量化
作圆
过一点可以作无数个圆
过两点可以作无数个圆
定理:过不在同一直线上的三个点确定一个圆
一个三角形的外接圆是唯一的.
注意:同一直线上的三个点不能作圆
点P在圆环内
r≤d≤R
R
r
P
作业:
《全品作业本》
27.2.1 点与圆的位置关系
27.2.1 点与圆的位置关系
课堂小结
例题讲解
获取新知
随堂演练
情景导入
第27章 圆
情境导入
你玩过飞镖吗?它的靶子是由一些圆组成的,你知道击中靶子上不同位置的成绩是如何计算的吗?
.
o
.
C
.
.
.
. B
.
.A
.
点与圆的位置关系有三种:
点在圆内,
点在圆上,
点在圆外.
观察下图中点和圆的位置关系有哪几种?
设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?
反过来,由d与r的数量关系,怎样判定点与圆的位置关系呢?
r=d
r<d
r>d
获取新知
点和圆的位置关系
r
P
d
P
r
d
P
r
d
R
r
P
点P在⊙O内
d
d=r
点P在⊙O外
d>r
点P在圆环内
r≤d≤R
数形结合:
位置关系
数量关系
⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
圆内
圆上
圆外
如何过一个点A作一个圆?过点A可以作多少个圆?
·
·
·
·
·
以不与A点重合的任意一点为圆心,以这个点到A点的距离为半径画圆即可;
A
可作无数个圆.
如何过两点A、B作一个圆?过两点可以作多少个圆?
·
·
·
·
A
B
作线段AB的垂直平分线,以其上任意一点为圆心,以这点和点A或B的距离为半径画圆即可;
可作无数个圆.
过不在同一直线上的三点能不能确定一个圆?
如何确定圆心位置?
A
B
C
D
E
G
F
●o
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
思考:如果A、B、C在同一条直线上,能画出经过这三点的圆吗?
l1
l2
A
B
C
P
如图,假设过同一条直线l上三点A、B、C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
有且只有
位置关系
定理:不在同一直线上的三个点确定一个圆.
已知:不在同一直线上的三点A、B、C.
求作: ⊙O,使它经过点A、B、C.
作法:
1、连结AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆。
所以⊙O就是所求作的圆.
O
N
M
F
E
A
B
C
已知△ABC,用直尺与圆规作出过A、B、C三点的圆.
A
B
C
O
三角形外接圆的作法:
(1)作三角形任意两边的垂直平分线,确定其交点;
(2)以该交点为圆心,以交点到三个顶点中任意一点的距离为半径作圆即可.
(1)任何一个三角形都有一个外接圆,而一个圆有无数个
内接三角形.一个三角形的外接圆是唯一的.
(2)锐角三角形的外心在三角形的内部;直角三角形的外
心在斜边中点处;钝角三角形的外心在三角形的外部.
(3)三角形的外心是三角形三条边的垂直平分线的交点,
它到三角形三个顶点的距离相等.
经过三角形三个顶点的圆就是这个三角形的外接圆,
三角形外接圆的圆心叫做这个三角形的外心.这个三角形叫做这个圆的内接三角形.
例题讲解
例1 如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以点A为圆心、3cm为半径画圆,并判断:
(1)点C与⊙A的位置关系;
(2)点B与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.
●
B
A
D
C
解:已知⊙A的半径r=3 cm.
(1) 因为 ,所以点C在⊙A上.
(2) 因为AB=5 cm>3 cm=r, 所以点B在⊙A外.
(3)因为 ,所以点D在⊙A内.
例2 如图,△ABC内接于⊙O,∠C=45°,AB=4,求⊙O 的半径.
解::如图,连接OA,OB,设⊙O的半径为r,
∵∠C=45°,∴∠AOB=2∠C=90°.
∴OA2+OB2=AB2,即r2+r2=42.
解得r1=2 ,r2=-2 (不符合题意,舍去).
∴⊙O的半径为2 .
还有其他的思路吗?
1.圆心为O的两个同心圆,半径分别为1和2,若OP= ,则点P在( )
A.大圆内 B.小圆内
C.小圆外 D.大圆内,小圆外
随堂演练
o
D
2.三角形的外心具有的性质是( )
A.到三边的距离相等. B.到三个顶点的距离相等.
C.外心在三角形的外. D.外心在三角形内.
3.等腰三角形底边上的高与一腰的垂直平分线的交点是( )
A.重心 B.垂心 C.外心 D.无法确定.
B
C
4.已知AB=4 cm,则过点A,B且半径为3 cm的圆有( )
A.1个 B.2个 C.3个 D.4个
B
5.如图,在△ABC中,点O在边AB上,且点O为△ABC的外心,求∠ACB的度数.
解:∵点O为△ABC的外心,
∴OA=OB=OC,
∴∠OAC=∠OCA,∠OCB=∠OBC.
∵∠OAC+∠OCA+∠OCB+∠OBC=180°,
∴∠OCA+∠OCB=90°,
即∠ACB=90°.
课堂小结
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d
作圆
过一点可以作无数个圆
过两点可以作无数个圆
定理:过不在同一直线上的三个点确定一个圆
一个三角形的外接圆是唯一的.
注意:同一直线上的三个点不能作圆
点P在圆环内
r≤d≤R
R
r
P
作业:
《全品作业本》
27.2.1 点与圆的位置关系
