湖北省七市2013届高三4月联考数学(理)试题
文档属性
| 名称 | 湖北省七市2013届高三4月联考数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 423.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-22 20:34:00 | ||
图片预览




文档简介
秘密★启用前
2013年湖北荆州、黄冈、襄阳、十堰、宜昌、孝感、恩施七市(州)
高三联合考试
数学(理工类)
本科目考试时间:2013年4月18日下午15:00-17:00
★祝考试顺利★
一、选择题:本大题共10小题,每小题5分,共50分.在每小题列出的四个选项中,只有一项是符合题目要求的.
1.设复数,其中a为实数,若z的实部为2,则z的虚部为
A.-i B.i C.-1 D.1
2.已知向量a=(2,1),b=(x,-2),若a∥b,则a+b=
A.(-2,-1) B.(2,1) C.(3,-1) D.(-3,1)
3.下列说法中不正确的个数是
①命题“x∈R,≤0”的否定是“∈R,>0”;
②若“pq”为假命题,则p、q均为假命题;
③“三个数a,b,c成等比数列”是“b=”的既不充分也不必要条件
A.O B.1 C.2 D.3
4.函数f(x)=2x-sinx的零点个数为
A.1 B.2 C.3 D.4
5.一个几何体的三视图如下左图所示,则此几何体的体积是
A.112 B.80 C.72 D.64
6.已知全集U=Z,Z为整数集,如上右图程序框图所示,集合A={x|框图中输出的x值},B={y|框图中输出的y值};当x=-1时,(CuA)B=
A.{-3,-1,5} B.{-3,-1,5,7} C.{-3,-1,7} D.{-3,-1,7,9}
7.我国第一艘航母“辽宁舰”在某次舰载机起降飞行训练中,有5架舰载机准备着舰.如果甲、乙两机必须相邻着舰,而丙、丁不能相邻着舰,那么不同的着舰方法有
A.12种 B.18种 C.24种 D.48种
8.如右图,矩形OABC内的阴影部分由曲线f(x)=sinx(x∈(0,))及直线x=a(a∈(0,))与x轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为,则a的值为
A. B. C. D.
9.如右图,一单位正方体形积木,平放于桌面上,并且在其上方放置若干个小正方体形积木摆成塔形,其中上面正方体中下底面的四个顶点是下面相邻正方体中上底面各边的中点,如果所有正方体暴露在外面部分的面积之和超过8.8,则正方体的个数至少是
A.6 8.7 C.8 D. 10
10.已知直线l:y=ax+1-a(a∈R).若存在实数a使得一条曲线与直线l有两个不同的交点,且以这两个交点为端点的线段长度恰好等于|a|,则称此曲线为直线l的“绝对曲线”.下面给出四条曲线方程:①y=-2 |x-1|;②y=;③(x-1)2+(y-1)2=1;④x2+3y2=4;则其中直线l的“绝对曲线”有
A.①④ B.②③ C.②④ D.②③④
二、填空题:本大题共6小题,考生共需作答5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清.模棱两可均不得分.
(一)必考题:(11-14题)
11.若tan=,∈(0,),则sin(2+)= .
12.点P(x,y)在不等式组表示的平面区域内,若点P(x,y)到直线y=kx-1(k>0)的最大距离为2,则k= .
13.已知抛物线y2=4x的焦点为F,过点P(2,0)的直线交抛物线于A(x1,y1)和B(x2,y2)两点.则:(I) y1 y2= ;(Ⅱ)三角形ABF面积的最小值是 .
14.挪威数学家阿贝尔,曾经根据阶梯形图形的两种不同分割(如下图),利用它们的面积关系发现了一个重要的恒等式一阿贝尔公式:
a1b1+a2b2+a3b3+…+anbn=a1(b1-b2)+L2(b2-b3)+L3(b3-b4)+…+Ln-1(bn-1-bn) +Lnbn
则其中:(I)L3= ;(Ⅱ)Ln= .
(二)选考题:请考生在第15、16两题中任选一题作答.如果全选,则按第15题作答结果计分.
15.(几何证明选讲)如右图,AB是⊙O的直径,P是AB延长线上的一点,过P作⊙O的切线,切点为C,PC=2,若∠CAP=30°,则⊙O的直径AB= .
16.(坐标系与参数方程)在直角坐标平面内,以坐标原点0为极点,x轴的非负半轴为极轴建立极坐标系,已知点M的极坐标为(4,),曲线C的参数方程为(为参数),则点M到曲线C上的点的距离的最小值为 .
三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)已知向量=(sin2x+2,cosx),=(1,2cosx),设函数
f(x)= ·.
(I)求f(x)的最小正周期与单调递增区间;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,若a=,f(A)=4,求b+c的最大值.
18.(本小题满分12分)数列{an}是公比为的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n·bn+1(为常数,且≠1).
(I)求数列{an}的通项公式及的值;
(Ⅱ)比较+++…+与了Sn的大小.
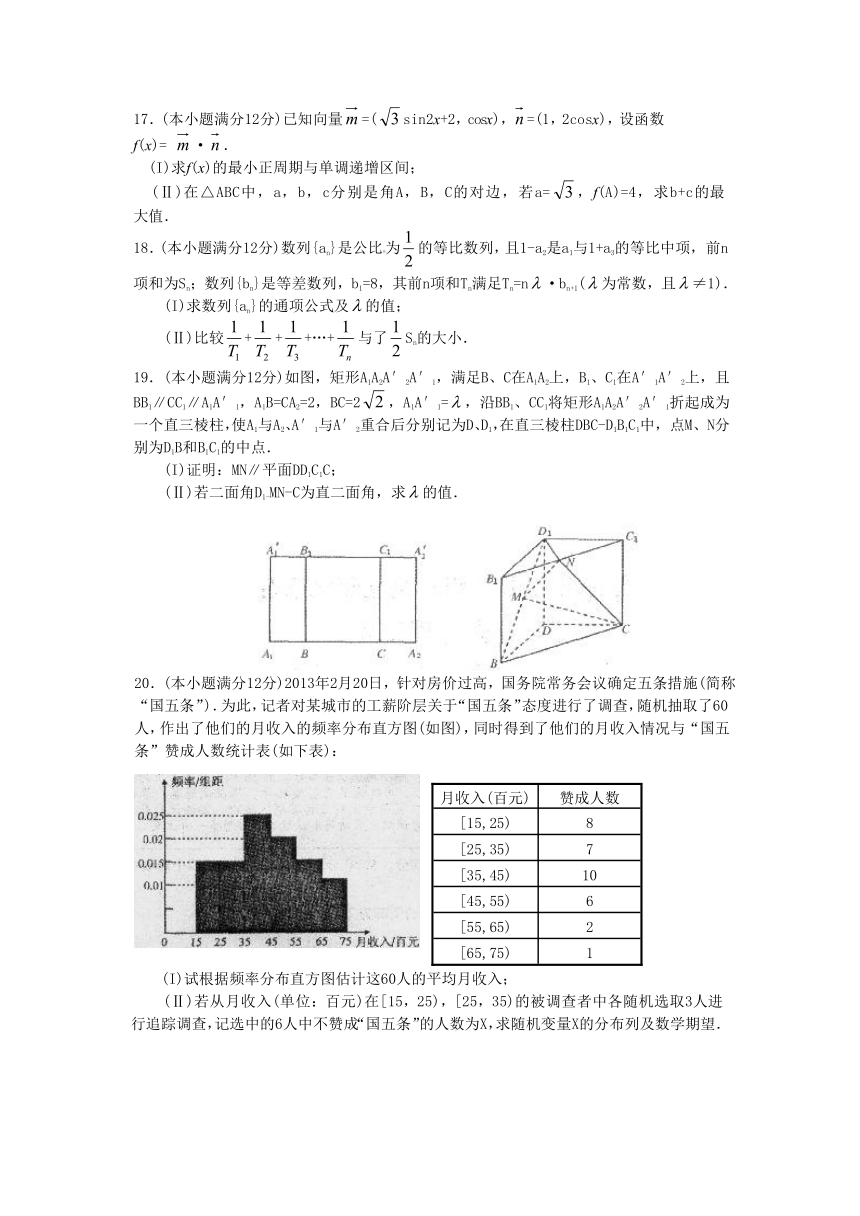
19.(本小题满分12分)如图,矩形A1A2A′2A′1,满足B、C在A1A2上,B1、C1在A′1A′2上,且BB1∥CC1∥A1A′1,A1B=CA2=2,BC=2,A1A′1=,沿BB1、CC1将矩形A1A2A′2A′1折起成为一个直三棱柱,使A1与A2、A′1与A′2重合后分别记为D、D1,在直三棱柱DBC-D1B1C1中,点M、N分别为D1B和B1C1的中点.
(I)证明:MN∥平面DD1C1C;
(Ⅱ)若二面角D1-MN-C为直二面角,求的值.
20.(本小题满分12分)2013年2月20日,针对房价过高,国务院常务会议确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了60人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如下表):
月收入(百元) 赞成人数
[15,25) 8
[25,35) 7
[35,45) 10
[45,55) 6
[55,65) 2
[65,75) 1
(I)试根据频率分布直方图估计这60人的平均月收入;
(Ⅱ)若从月收入(单位:百元)在[15,25),[25,35)的被调查者中各随机选取3人进行追踪调查,记选中的6人中不赞成“国五条”的人数为X,求随机变量X的分布列及数学期望.
21.(本小题满分13分)在矩形ABCD中,|AB|=2,|AD|=2,E、F、G、H分别为矩形四条边的中点,以HF、GE所在直线分别为x,y轴建立直角坐标系(如图所示).若R、R′分别在线段0F、CF上,且==.
(Ⅰ)求证:直线ER与GR′的交点P在椭圆:+=1上;
(Ⅱ)若M、N为椭圆上的两点,且直线GM与直线GN的斜率之积为,求证:直线MN过定点;并求△GMN面积的最大值.
22.(本小题满分14分)已知函数f(x)=lnx,g(x)=k·.
(I)求函数F(x)= f(x)- g(x)的单调区间;
(Ⅱ)当x>1时,函数f(x)> g(x)恒成立,求实数k的取值范围;
(Ⅲ)设正实数a1,a2,a3,…,an满足a1+a2+a3+…+an=1,
求证:ln(1+)+ln(1+)+…+ln(1+)>.
2013年七市联考数学试题(理工类)(B卷)
参考答案
一、选择题: CABAB DCBAD
二、填空题:11. 12. 13.(Ⅰ) (Ⅱ)
14.(Ⅰ)(Ⅱ) 15. 16.
(注:填空题中有两个空的,第一个空2分,第二个空3分)
三、解答题
17.解:(Ⅰ)
……………3分
∴的最小正周期 ……………4分
由得
∴的单调递增区间为 ……………6分
(Ⅱ)由得,
∵ ∴ ∴ , ……………8分
法一:又 ,
∴当时,最大为 ……………12分
法二:即
;当且仅当时等号成立。 ……………12分
18.解:(Ⅰ)由题意,即
解得,∴ ……………2分
又,即 ……………4分
解得 或(舍)∴ ……………6分
(Ⅱ)由(Ⅰ)知
∴ ① ……………8分
又,
∴ ②…11分
由①②可知 ……………12分
19.解:(Ⅰ)证:连结DB1 、DC1 ∵四边形DBB1D1为矩形,M为D1B的中点 ……2分
∴M是DB1与D1B的交点,且M为DB1的中点
∴MN∥DC1,∴MN∥平面DD1C1C ……………4分
(Ⅱ)解:四边形为矩形,B.C在A1A2上,B1.C1在上,
且BB1∥CC1∥,A1B = CA2 = 2,,
∴∠BDC = 90° ……………6分
以DB、DC、DD1所在直线分别为x.y.z轴建立直角坐标系,则
D(0,0,0),B(2,0,0),C(0,2,0),D1(0,0,),B1(2,0,),C1(0,2,)
点M、N分别为D1B和B1C1的中点,∴
设平面D1MN的法向量为m = (x,y,z),则
,
令x = 1得:
即 ……………8分
设平面MNC的法向量为n = (x,y,z),则
,令z = 1得:
即 ……………10分
∵二面角D1-MN-C为直二面角 ∴m⊥n,故,解得:
∴二面角D1-MN-C为直二面角时,. ……………12分
20.解:(Ⅰ)这人的月平均收入为
(百元) ……………4分
(Ⅱ)根据频率分布直方图可知
的人数为人
的人数为人 ……………6分
的所有取值可能为
…… ……10分
∴的分布列为
∴ ……………12分
21.解:(Ⅰ)∵,∴, ……………1分
又 则直线的方程为 ① ……………2分
又 则直线的方程为 ②
由①②得
∵
∴直线与的交点在椭圆上 ……………4分
(Ⅱ)①当直线的斜率不存在时,设
不妨取 ∴ ,不合题意……………5分
②当直线的斜率存在时,设
联立方程 得
则
…………7分
又
即
将代入上式得
解得或(舍)
∴直线过定点 ……………10分
∴,点到直线的距离为
∴
由及知:,令 即
∴ 当且仅当时,……13分
22、解:(Ⅰ) --- 1分
由的判别式
①当即时,恒成立,则在单调递增 ……2分
②当时,在恒成立,则在单调递增 ……3分
③当时,方程的两正根为
则在单调递增,单调递减,单调递增
综上,当时,只有单调递增区间
当时,单调递增区间为,
单调递减区间为 …… 5分
(Ⅱ)即时,恒成立
当时,在单调递增 ∴当时,满足条件 …7分
当时,在单调递减
则在单调递减
此时不满足条件
故实数的取值范围为 …… 9分
(Ⅲ)由(2)知,在恒成立
令 则 …… 10分
∴ …… 11分
又
∴ ……13分
∴ …… 14分
注:解答题中,若有不同解法,只要思路清晰,解法正确,请酌情给分。
2013年湖北荆州、黄冈、襄阳、十堰、宜昌、孝感、恩施七市(州)
高三联合考试
数学(理工类)
本科目考试时间:2013年4月18日下午15:00-17:00
★祝考试顺利★
一、选择题:本大题共10小题,每小题5分,共50分.在每小题列出的四个选项中,只有一项是符合题目要求的.
1.设复数,其中a为实数,若z的实部为2,则z的虚部为
A.-i B.i C.-1 D.1
2.已知向量a=(2,1),b=(x,-2),若a∥b,则a+b=
A.(-2,-1) B.(2,1) C.(3,-1) D.(-3,1)
3.下列说法中不正确的个数是
①命题“x∈R,≤0”的否定是“∈R,>0”;
②若“pq”为假命题,则p、q均为假命题;
③“三个数a,b,c成等比数列”是“b=”的既不充分也不必要条件
A.O B.1 C.2 D.3
4.函数f(x)=2x-sinx的零点个数为
A.1 B.2 C.3 D.4
5.一个几何体的三视图如下左图所示,则此几何体的体积是
A.112 B.80 C.72 D.64
6.已知全集U=Z,Z为整数集,如上右图程序框图所示,集合A={x|框图中输出的x值},B={y|框图中输出的y值};当x=-1时,(CuA)B=
A.{-3,-1,5} B.{-3,-1,5,7} C.{-3,-1,7} D.{-3,-1,7,9}
7.我国第一艘航母“辽宁舰”在某次舰载机起降飞行训练中,有5架舰载机准备着舰.如果甲、乙两机必须相邻着舰,而丙、丁不能相邻着舰,那么不同的着舰方法有
A.12种 B.18种 C.24种 D.48种
8.如右图,矩形OABC内的阴影部分由曲线f(x)=sinx(x∈(0,))及直线x=a(a∈(0,))与x轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为,则a的值为
A. B. C. D.
9.如右图,一单位正方体形积木,平放于桌面上,并且在其上方放置若干个小正方体形积木摆成塔形,其中上面正方体中下底面的四个顶点是下面相邻正方体中上底面各边的中点,如果所有正方体暴露在外面部分的面积之和超过8.8,则正方体的个数至少是
A.6 8.7 C.8 D. 10
10.已知直线l:y=ax+1-a(a∈R).若存在实数a使得一条曲线与直线l有两个不同的交点,且以这两个交点为端点的线段长度恰好等于|a|,则称此曲线为直线l的“绝对曲线”.下面给出四条曲线方程:①y=-2 |x-1|;②y=;③(x-1)2+(y-1)2=1;④x2+3y2=4;则其中直线l的“绝对曲线”有
A.①④ B.②③ C.②④ D.②③④
二、填空题:本大题共6小题,考生共需作答5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清.模棱两可均不得分.
(一)必考题:(11-14题)
11.若tan=,∈(0,),则sin(2+)= .
12.点P(x,y)在不等式组表示的平面区域内,若点P(x,y)到直线y=kx-1(k>0)的最大距离为2,则k= .
13.已知抛物线y2=4x的焦点为F,过点P(2,0)的直线交抛物线于A(x1,y1)和B(x2,y2)两点.则:(I) y1 y2= ;(Ⅱ)三角形ABF面积的最小值是 .
14.挪威数学家阿贝尔,曾经根据阶梯形图形的两种不同分割(如下图),利用它们的面积关系发现了一个重要的恒等式一阿贝尔公式:
a1b1+a2b2+a3b3+…+anbn=a1(b1-b2)+L2(b2-b3)+L3(b3-b4)+…+Ln-1(bn-1-bn) +Lnbn
则其中:(I)L3= ;(Ⅱ)Ln= .
(二)选考题:请考生在第15、16两题中任选一题作答.如果全选,则按第15题作答结果计分.
15.(几何证明选讲)如右图,AB是⊙O的直径,P是AB延长线上的一点,过P作⊙O的切线,切点为C,PC=2,若∠CAP=30°,则⊙O的直径AB= .
16.(坐标系与参数方程)在直角坐标平面内,以坐标原点0为极点,x轴的非负半轴为极轴建立极坐标系,已知点M的极坐标为(4,),曲线C的参数方程为(为参数),则点M到曲线C上的点的距离的最小值为 .
三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)已知向量=(sin2x+2,cosx),=(1,2cosx),设函数
f(x)= ·.
(I)求f(x)的最小正周期与单调递增区间;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,若a=,f(A)=4,求b+c的最大值.
18.(本小题满分12分)数列{an}是公比为的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n·bn+1(为常数,且≠1).
(I)求数列{an}的通项公式及的值;
(Ⅱ)比较+++…+与了Sn的大小.
19.(本小题满分12分)如图,矩形A1A2A′2A′1,满足B、C在A1A2上,B1、C1在A′1A′2上,且BB1∥CC1∥A1A′1,A1B=CA2=2,BC=2,A1A′1=,沿BB1、CC1将矩形A1A2A′2A′1折起成为一个直三棱柱,使A1与A2、A′1与A′2重合后分别记为D、D1,在直三棱柱DBC-D1B1C1中,点M、N分别为D1B和B1C1的中点.
(I)证明:MN∥平面DD1C1C;
(Ⅱ)若二面角D1-MN-C为直二面角,求的值.
20.(本小题满分12分)2013年2月20日,针对房价过高,国务院常务会议确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了60人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如下表):
月收入(百元) 赞成人数
[15,25) 8
[25,35) 7
[35,45) 10
[45,55) 6
[55,65) 2
[65,75) 1
(I)试根据频率分布直方图估计这60人的平均月收入;
(Ⅱ)若从月收入(单位:百元)在[15,25),[25,35)的被调查者中各随机选取3人进行追踪调查,记选中的6人中不赞成“国五条”的人数为X,求随机变量X的分布列及数学期望.
21.(本小题满分13分)在矩形ABCD中,|AB|=2,|AD|=2,E、F、G、H分别为矩形四条边的中点,以HF、GE所在直线分别为x,y轴建立直角坐标系(如图所示).若R、R′分别在线段0F、CF上,且==.
(Ⅰ)求证:直线ER与GR′的交点P在椭圆:+=1上;
(Ⅱ)若M、N为椭圆上的两点,且直线GM与直线GN的斜率之积为,求证:直线MN过定点;并求△GMN面积的最大值.
22.(本小题满分14分)已知函数f(x)=lnx,g(x)=k·.
(I)求函数F(x)= f(x)- g(x)的单调区间;
(Ⅱ)当x>1时,函数f(x)> g(x)恒成立,求实数k的取值范围;
(Ⅲ)设正实数a1,a2,a3,…,an满足a1+a2+a3+…+an=1,
求证:ln(1+)+ln(1+)+…+ln(1+)>.
2013年七市联考数学试题(理工类)(B卷)
参考答案
一、选择题: CABAB DCBAD
二、填空题:11. 12. 13.(Ⅰ) (Ⅱ)
14.(Ⅰ)(Ⅱ) 15. 16.
(注:填空题中有两个空的,第一个空2分,第二个空3分)
三、解答题
17.解:(Ⅰ)
……………3分
∴的最小正周期 ……………4分
由得
∴的单调递增区间为 ……………6分
(Ⅱ)由得,
∵ ∴ ∴ , ……………8分
法一:又 ,
∴当时,最大为 ……………12分
法二:即
;当且仅当时等号成立。 ……………12分
18.解:(Ⅰ)由题意,即
解得,∴ ……………2分
又,即 ……………4分
解得 或(舍)∴ ……………6分
(Ⅱ)由(Ⅰ)知
∴ ① ……………8分
又,
∴ ②…11分
由①②可知 ……………12分
19.解:(Ⅰ)证:连结DB1 、DC1 ∵四边形DBB1D1为矩形,M为D1B的中点 ……2分
∴M是DB1与D1B的交点,且M为DB1的中点
∴MN∥DC1,∴MN∥平面DD1C1C ……………4分
(Ⅱ)解:四边形为矩形,B.C在A1A2上,B1.C1在上,
且BB1∥CC1∥,A1B = CA2 = 2,,
∴∠BDC = 90° ……………6分
以DB、DC、DD1所在直线分别为x.y.z轴建立直角坐标系,则
D(0,0,0),B(2,0,0),C(0,2,0),D1(0,0,),B1(2,0,),C1(0,2,)
点M、N分别为D1B和B1C1的中点,∴
设平面D1MN的法向量为m = (x,y,z),则
,
令x = 1得:
即 ……………8分
设平面MNC的法向量为n = (x,y,z),则
,令z = 1得:
即 ……………10分
∵二面角D1-MN-C为直二面角 ∴m⊥n,故,解得:
∴二面角D1-MN-C为直二面角时,. ……………12分
20.解:(Ⅰ)这人的月平均收入为
(百元) ……………4分
(Ⅱ)根据频率分布直方图可知
的人数为人
的人数为人 ……………6分
的所有取值可能为
…… ……10分
∴的分布列为
∴ ……………12分
21.解:(Ⅰ)∵,∴, ……………1分
又 则直线的方程为 ① ……………2分
又 则直线的方程为 ②
由①②得
∵
∴直线与的交点在椭圆上 ……………4分
(Ⅱ)①当直线的斜率不存在时,设
不妨取 ∴ ,不合题意……………5分
②当直线的斜率存在时,设
联立方程 得
则
…………7分
又
即
将代入上式得
解得或(舍)
∴直线过定点 ……………10分
∴,点到直线的距离为
∴
由及知:,令 即
∴ 当且仅当时,……13分
22、解:(Ⅰ) --- 1分
由的判别式
①当即时,恒成立,则在单调递增 ……2分
②当时,在恒成立,则在单调递增 ……3分
③当时,方程的两正根为
则在单调递增,单调递减,单调递增
综上,当时,只有单调递增区间
当时,单调递增区间为,
单调递减区间为 …… 5分
(Ⅱ)即时,恒成立
当时,在单调递增 ∴当时,满足条件 …7分
当时,在单调递减
则在单调递减
此时不满足条件
故实数的取值范围为 …… 9分
(Ⅲ)由(2)知,在恒成立
令 则 …… 10分
∴ …… 11分
又
∴ ……13分
∴ …… 14分
注:解答题中,若有不同解法,只要思路清晰,解法正确,请酌情给分。
同课章节目录
