华师大版数学八年级下册同步课件:16.3 可化为一元一次方程的分式方程(共23张PPT)
文档属性
| 名称 | 华师大版数学八年级下册同步课件:16.3 可化为一元一次方程的分式方程(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 839.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 16:16:35 | ||
图片预览








文档简介
(共23张PPT)
第16章 分式
16.3 可化为一元一次方程的分式方程
情景导入
轮船顺水航行80千米所需的时
间和逆水航行60千米所需的时
间相同.已知水流的速度是3千
米/时,求轮船在静水中的速度.设轮船在静水中的速度x千米/时,根据题意可列方程 .
这个方程是我们以前学过的方程吗?它与一元一次方程有什么区别?
获取新知
为了帮助遭受自然灾害的地区重建家园,某校团总支号召同学们自愿捐款.已知第一次捐款总额为4800元,第二次捐款总额为5000元,第二次捐款人数比第一次多20人,而且两次人均捐款
额恰好相等.如果设第一次捐
款人数为x人,那么x应满足
怎样的方程?
由上面的问题,我们得到了2个方程,它们有什么共同特点?
分母中都含有未知数.
分式方程的概念
分式方程的特征
分母中含有未知数的方程叫做分式方程.
(1)是等式;
(2)方程中含有分母;
(3)分母中含有未知数.
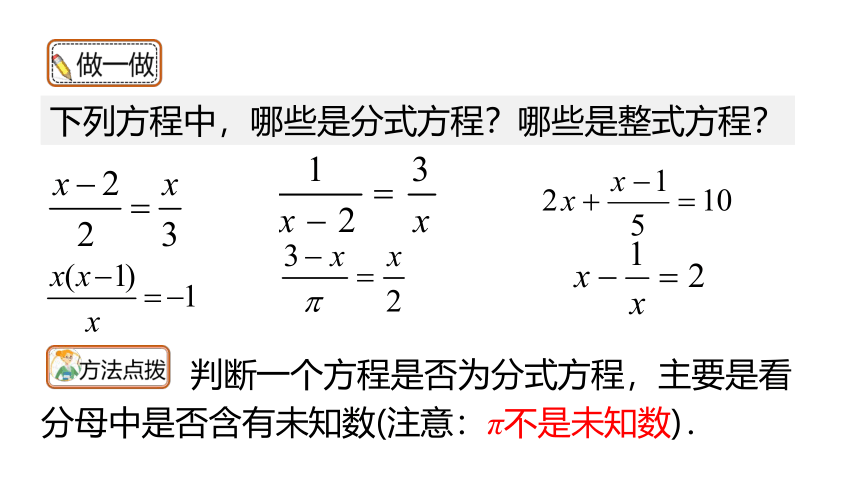
下列方程中,哪些是分式方程?哪些是整式方程?
判断一个方程是否为分式方程,主要是看分母中是否含有未知数(注意:π不是未知数).
怎样解分式方程呢?有没有办法可以去掉分式方程中的分母把它转化为整式方程呢?
试动手求解方程 .
解:方程两边同乘以(x+3)(x-3),约去分母得80(x-3)=60(x+3).
解这个整式方程,得x=21.
所以轮船在静水中的速度为21千米/时.
求解方程 .
上述解分式方程的过程,实质上是将方程的两边都乘以同一个整式,约去分母,把分式方程转化为整式方程来解.所乘的整式通常取方程中出现的各分式的最简公分母.
例1
解方程:
解:方程两边同乘以 ,约去分母,得x+1=2.
解得: x=1.
能不能说x=1就是原分式方程的解呢?
例题讲解
当x=1时,原分式方程左边和右边的分母都是0,方程中出现的两个分式都没意义,因此,x=1不是原分式方程的解,应当舍去,所以原分式方程无解.
分析:
在将分式方程变形为整式方程时,方程两边同乘以一个含未知数的整式,并约去了分母,有时可能产生不适合原分式方程的解,这种根通常叫增根,因此在解分式方程时必须进行检验.
因为我们在去分母时,方程的两边都乘以公分母时,我们并没有考虑公分母是否是为0,所以使方程有了产生了增根的可能。 所以我们检验时不一定代入方程的左右两边,只要代入最简公分母检验就可,值为0时为增根,不为0时则是方程的解。
为何一定要检验呢?
例2 解方程:
解:方程两边同乘以x(x-7),约去分母,
得:100(x-7)=30x.
解得x=10.
检验:把x=10代入x(x-7),得
10×(10-7)≠0.
所以,x=10是原方程的解.
解分式方程的步骤
①去分母:先确定最简公分母,它是指方程两边所有分母的最简公分母,确定方法与通分时确定最简公分母的方法一致;
②解方程:解去分母后得到的整式方程;
③验根:验根是解分式方程的必要步骤,把整式方程的根代入最简公分母,值为零时,为增根,否则为原方程的根。
④下结论:写出分式方程根的情况。
例3 用计算机处理数据,为了防止数据输入出错,某研究室安排两位程序操作员各输入一遍,比较两人的输入是否一致.两人各输入2640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完.这两个操作员每分钟各能输入多少个数据?
设乙每分钟能输入x个数据,则甲每分钟能 输入2x个数据,根据题意,得
解得 x=11.
经检验,x= 11是原方程的解.
当x=11时,2x=22.所以乙用了240分钟,甲用了120分钟,甲比乙少用了120分钟,符合题意.
答:甲每分钟能输入22个数据,乙每分钟能输入11 个数据.
解:
随堂演练
A
A
1.下列关于x的方程中,是分式方程的有( )
2.若x=4是分式方程 的根则a的值为 ( )
A.1个 B.2个 C.3个 D.4个
A.6 B.-6 C.4 D.-4
解:去分母,得 .
去括号,得 .
解得x= .
检验:把x= 代入2(x+2),得 .
所以,原方程的解是x= .
2(2x+5)-1=2x+4
4x+10-1=2x+4
3.解方程:
2×( +2)≠0
解:(1)方程两边同乘以x(x-1),
得x2-2(x-1)=x(x-1).
解得x=2.
检验:当x=2时,x(x-1)≠0,
所以x=2是原分式方程的解.
4.解方程:(1) (2)
解:
4.解方程:(1) (2)
(2)将原方程整理得:
方程两边同乘以3x-1,
得3(3x-1)-1=2.
去括号,得9x-3-1=2.
解得x=
检验:把x= 代入3x-1,
得3× -1=1≠0.所以x= 是原方程的解.
x=-18(不合题意,舍去),
解:设船在静水中的速度为x千米/小时,根据题意得
解得 x=±18.
经检验x=18是原方程的解且符合题意.
答:船在静水中的速度为18千米/小时.
方程两边同乘(x-2)(x+2)得
80x+160 -80x+160=x2 -4.
5.一轮船往返于A、B两地之间,顺水比逆水快1小时到达.已知A、B两地相距80千米,水流速度是2千米/小时,求轮船在静水中的速度.
课堂小结
分式方程
整式方程
去分母转化
1.化成整式方程
2.解整式方程
3.验根
4.下结论
分式方程
定义
解法
基本思路
步 骤
分母中含有未知数的方程
应用
根据实际问题构建对应的分式方程
第16章 分式
16.3 可化为一元一次方程的分式方程
情景导入
轮船顺水航行80千米所需的时
间和逆水航行60千米所需的时
间相同.已知水流的速度是3千
米/时,求轮船在静水中的速度.设轮船在静水中的速度x千米/时,根据题意可列方程 .
这个方程是我们以前学过的方程吗?它与一元一次方程有什么区别?
获取新知
为了帮助遭受自然灾害的地区重建家园,某校团总支号召同学们自愿捐款.已知第一次捐款总额为4800元,第二次捐款总额为5000元,第二次捐款人数比第一次多20人,而且两次人均捐款
额恰好相等.如果设第一次捐
款人数为x人,那么x应满足
怎样的方程?
由上面的问题,我们得到了2个方程,它们有什么共同特点?
分母中都含有未知数.
分式方程的概念
分式方程的特征
分母中含有未知数的方程叫做分式方程.
(1)是等式;
(2)方程中含有分母;
(3)分母中含有未知数.
下列方程中,哪些是分式方程?哪些是整式方程?
判断一个方程是否为分式方程,主要是看分母中是否含有未知数(注意:π不是未知数).
怎样解分式方程呢?有没有办法可以去掉分式方程中的分母把它转化为整式方程呢?
试动手求解方程 .
解:方程两边同乘以(x+3)(x-3),约去分母得80(x-3)=60(x+3).
解这个整式方程,得x=21.
所以轮船在静水中的速度为21千米/时.
求解方程 .
上述解分式方程的过程,实质上是将方程的两边都乘以同一个整式,约去分母,把分式方程转化为整式方程来解.所乘的整式通常取方程中出现的各分式的最简公分母.
例1
解方程:
解:方程两边同乘以 ,约去分母,得x+1=2.
解得: x=1.
能不能说x=1就是原分式方程的解呢?
例题讲解
当x=1时,原分式方程左边和右边的分母都是0,方程中出现的两个分式都没意义,因此,x=1不是原分式方程的解,应当舍去,所以原分式方程无解.
分析:
在将分式方程变形为整式方程时,方程两边同乘以一个含未知数的整式,并约去了分母,有时可能产生不适合原分式方程的解,这种根通常叫增根,因此在解分式方程时必须进行检验.
因为我们在去分母时,方程的两边都乘以公分母时,我们并没有考虑公分母是否是为0,所以使方程有了产生了增根的可能。 所以我们检验时不一定代入方程的左右两边,只要代入最简公分母检验就可,值为0时为增根,不为0时则是方程的解。
为何一定要检验呢?
例2 解方程:
解:方程两边同乘以x(x-7),约去分母,
得:100(x-7)=30x.
解得x=10.
检验:把x=10代入x(x-7),得
10×(10-7)≠0.
所以,x=10是原方程的解.
解分式方程的步骤
①去分母:先确定最简公分母,它是指方程两边所有分母的最简公分母,确定方法与通分时确定最简公分母的方法一致;
②解方程:解去分母后得到的整式方程;
③验根:验根是解分式方程的必要步骤,把整式方程的根代入最简公分母,值为零时,为增根,否则为原方程的根。
④下结论:写出分式方程根的情况。
例3 用计算机处理数据,为了防止数据输入出错,某研究室安排两位程序操作员各输入一遍,比较两人的输入是否一致.两人各输入2640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完.这两个操作员每分钟各能输入多少个数据?
设乙每分钟能输入x个数据,则甲每分钟能 输入2x个数据,根据题意,得
解得 x=11.
经检验,x= 11是原方程的解.
当x=11时,2x=22.所以乙用了240分钟,甲用了120分钟,甲比乙少用了120分钟,符合题意.
答:甲每分钟能输入22个数据,乙每分钟能输入11 个数据.
解:
随堂演练
A
A
1.下列关于x的方程中,是分式方程的有( )
2.若x=4是分式方程 的根则a的值为 ( )
A.1个 B.2个 C.3个 D.4个
A.6 B.-6 C.4 D.-4
解:去分母,得 .
去括号,得 .
解得x= .
检验:把x= 代入2(x+2),得 .
所以,原方程的解是x= .
2(2x+5)-1=2x+4
4x+10-1=2x+4
3.解方程:
2×( +2)≠0
解:(1)方程两边同乘以x(x-1),
得x2-2(x-1)=x(x-1).
解得x=2.
检验:当x=2时,x(x-1)≠0,
所以x=2是原分式方程的解.
4.解方程:(1) (2)
解:
4.解方程:(1) (2)
(2)将原方程整理得:
方程两边同乘以3x-1,
得3(3x-1)-1=2.
去括号,得9x-3-1=2.
解得x=
检验:把x= 代入3x-1,
得3× -1=1≠0.所以x= 是原方程的解.
x=-18(不合题意,舍去),
解:设船在静水中的速度为x千米/小时,根据题意得
解得 x=±18.
经检验x=18是原方程的解且符合题意.
答:船在静水中的速度为18千米/小时.
方程两边同乘(x-2)(x+2)得
80x+160 -80x+160=x2 -4.
5.一轮船往返于A、B两地之间,顺水比逆水快1小时到达.已知A、B两地相距80千米,水流速度是2千米/小时,求轮船在静水中的速度.
课堂小结
分式方程
整式方程
去分母转化
1.化成整式方程
2.解整式方程
3.验根
4.下结论
分式方程
定义
解法
基本思路
步 骤
分母中含有未知数的方程
应用
根据实际问题构建对应的分式方程
