华师大版数学八年级下册同步课件:17.2.2 函数的图象(共16张PPT)
文档属性
| 名称 | 华师大版数学八年级下册同步课件:17.2.2 函数的图象(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 526.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 11:18:28 | ||
图片预览





文档简介
(共16张PPT)
第17章 函数及其图象
17.2.2 函数的图象
情境导入
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
气温T( C)
2
4
6
8
-2
0
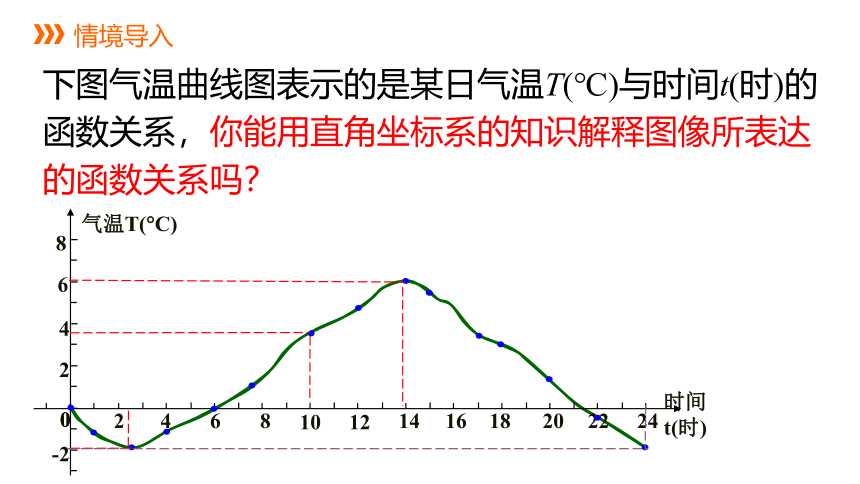
下图气温曲线图表示的是某日气温T(℃)与时间t(时)的函数关系,你能用直角坐标系的知识解释图像所表达的函数关系吗?
在上面的图形中,有一个直角坐标系,它的横轴表示时间,它的纵轴表示气温,这一气温曲线图实质上给出某日气温T(℃)与时间t(时)的函数关系,因为对于一日24小时的任何一刻,都有唯一的温度与之对应.
获取新知
例如,上午10时的气温是2 ℃,表现在曲线上,就是可以找到这样的对应点,它的坐标是(10,2),也就是说,当t=10时时,对应的函数值T=2 ℃.由于坐标平面上的点与有序实数对是一一对应的关系,因此,气温曲线图是由许许多多的点(t,T)组成的.
从上面的气温曲线图我们可以看出,图象可以非常直观、非常形象地表示出函数关系,利用函数图象上提供的信息我们可以方便地解决一些问题。
你能根据上面讲解给出函数图象的定义吗?
定义:一般来说,函数的图象是由平面直角坐标系中一系列的点组成的,图象上每一点的坐标(x,y)代表了函数的一对对应值,它的横坐标x表示自变量的某一个值,纵坐标y表示与该自变量的值对应的函数值.
如何画出一个函数的图像呢?
例题讲解
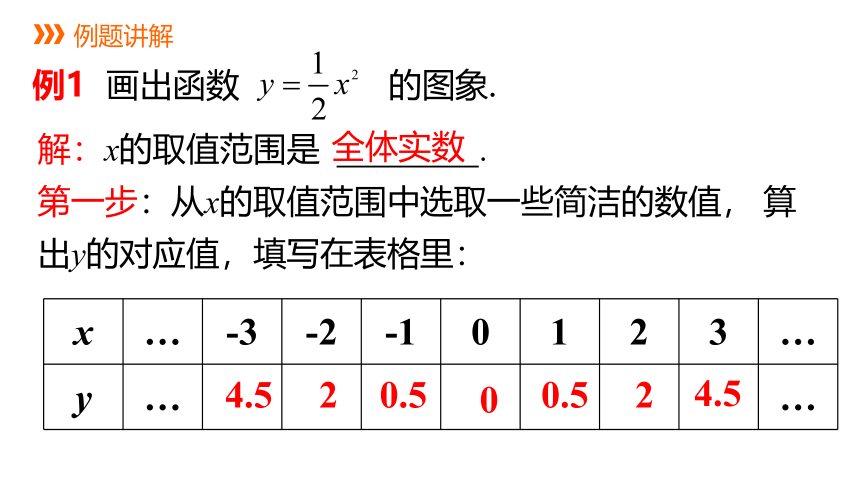
例1 画出函数 的图象.
x … -3 -2 -1 0 1 2 3 …
y … …
4.5
2
0.5
0.5
2
4.5
0
解:x的取值范围是 .
第一步:从x的取值范围中选取一些简洁的数值, 算出y的对应值,填写在表格里:
全体实数
第二步:根据表中数值描点(x,y);
第三步:用光滑的曲线依次把这些点连起来,便可以得到这个函数的图像。
第一步,列表——表中给出一些自变量的值及
其 ;
第二步,描点——在平面直角坐标系中,以自
变量的值为 ,相应的函数值为 ,
描出表格中各数对对应的各点;
第三步:连线——按照横坐标 的顺序,
把所描出的各点用 连接起来.
对应的函数值
横坐标
纵坐标
平滑曲线
由小到大
画函数图象的一般步骤:
例2 王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时),
看图回答下列问题:
解:由图象可知:(1)小强出发0分钟时,爷爷已经爬山60米,因此小强让爷爷先上60米.
解:山顶离山脚的距离是 300米,小强先爬上山顶.
(1)小强让爷爷先上多少米?
(2)山顶高多少米?谁先爬上山顶?
解:因为小强和爷爷路程相等时是8分钟,所以小强用了8分钟追上爷爷.
(3)小强需多少时间追上爷爷?
O
1.已知点A(2,3)在函数y=ax2-x+1的图象上,则a=( )
A.1 B.-1 C.2 D.-2
A
随堂演练
2.把下面画函数y=-x+2的图象的过程补充完整.
解:(1)列表为:
(2)画出的函数图象为:
x … -2 -1 0 1 2 3 …
y=-x+2 … …
4 3 2 1 0 -1
y=-x+2
3.下图反映的过程是小明从家去菜地浇水,又去玉米地锄草,然后回家.其中x表示时间,y表示小明离家的距离.小明家、菜地、玉米地在同一条直线上.
(1)小明从家到菜地用了_____分钟;菜地离小明家有_____千米.
(2)小明给菜地浇水用了_____分钟.
(3)小明从菜地到玉米地用了____分钟;菜地离玉米地有____千米.
(4)小明给玉米地锄草用了_____分钟.
(5)玉米地离小明家有___千米;小明从玉米地回家的
平均速度是____千米/分.
15
1.1
10
12
0.9
18
2
课堂小结
函数图象的定义
函数的图象
从图象获取信息
函数图象的画法:
列表、描点、连线
第17章 函数及其图象
17.2.2 函数的图象
情境导入
时间t(时)
8
10
2
4
6
12
14
16
18
20
22
24
0
气温T( C)
2
4
6
8
-2
0
下图气温曲线图表示的是某日气温T(℃)与时间t(时)的函数关系,你能用直角坐标系的知识解释图像所表达的函数关系吗?
在上面的图形中,有一个直角坐标系,它的横轴表示时间,它的纵轴表示气温,这一气温曲线图实质上给出某日气温T(℃)与时间t(时)的函数关系,因为对于一日24小时的任何一刻,都有唯一的温度与之对应.
获取新知
例如,上午10时的气温是2 ℃,表现在曲线上,就是可以找到这样的对应点,它的坐标是(10,2),也就是说,当t=10时时,对应的函数值T=2 ℃.由于坐标平面上的点与有序实数对是一一对应的关系,因此,气温曲线图是由许许多多的点(t,T)组成的.
从上面的气温曲线图我们可以看出,图象可以非常直观、非常形象地表示出函数关系,利用函数图象上提供的信息我们可以方便地解决一些问题。
你能根据上面讲解给出函数图象的定义吗?
定义:一般来说,函数的图象是由平面直角坐标系中一系列的点组成的,图象上每一点的坐标(x,y)代表了函数的一对对应值,它的横坐标x表示自变量的某一个值,纵坐标y表示与该自变量的值对应的函数值.
如何画出一个函数的图像呢?
例题讲解
例1 画出函数 的图象.
x … -3 -2 -1 0 1 2 3 …
y … …
4.5
2
0.5
0.5
2
4.5
0
解:x的取值范围是 .
第一步:从x的取值范围中选取一些简洁的数值, 算出y的对应值,填写在表格里:
全体实数
第二步:根据表中数值描点(x,y);
第三步:用光滑的曲线依次把这些点连起来,便可以得到这个函数的图像。
第一步,列表——表中给出一些自变量的值及
其 ;
第二步,描点——在平面直角坐标系中,以自
变量的值为 ,相应的函数值为 ,
描出表格中各数对对应的各点;
第三步:连线——按照横坐标 的顺序,
把所描出的各点用 连接起来.
对应的函数值
横坐标
纵坐标
平滑曲线
由小到大
画函数图象的一般步骤:
例2 王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时),
看图回答下列问题:
解:由图象可知:(1)小强出发0分钟时,爷爷已经爬山60米,因此小强让爷爷先上60米.
解:山顶离山脚的距离是 300米,小强先爬上山顶.
(1)小强让爷爷先上多少米?
(2)山顶高多少米?谁先爬上山顶?
解:因为小强和爷爷路程相等时是8分钟,所以小强用了8分钟追上爷爷.
(3)小强需多少时间追上爷爷?
O
1.已知点A(2,3)在函数y=ax2-x+1的图象上,则a=( )
A.1 B.-1 C.2 D.-2
A
随堂演练
2.把下面画函数y=-x+2的图象的过程补充完整.
解:(1)列表为:
(2)画出的函数图象为:
x … -2 -1 0 1 2 3 …
y=-x+2 … …
4 3 2 1 0 -1
y=-x+2
3.下图反映的过程是小明从家去菜地浇水,又去玉米地锄草,然后回家.其中x表示时间,y表示小明离家的距离.小明家、菜地、玉米地在同一条直线上.
(1)小明从家到菜地用了_____分钟;菜地离小明家有_____千米.
(2)小明给菜地浇水用了_____分钟.
(3)小明从菜地到玉米地用了____分钟;菜地离玉米地有____千米.
(4)小明给玉米地锄草用了_____分钟.
(5)玉米地离小明家有___千米;小明从玉米地回家的
平均速度是____千米/分.
15
1.1
10
12
0.9
18
2
课堂小结
函数图象的定义
函数的图象
从图象获取信息
函数图象的画法:
列表、描点、连线
