华师大版数学八年级下册同步课件:17.1 第2课时 自变量的取值范围及函数值(共19张PPT)
文档属性
| 名称 | 华师大版数学八年级下册同步课件:17.1 第2课时 自变量的取值范围及函数值(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 883.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 16:18:41 | ||
图片预览



文档简介
(共19张PPT)
第17章 函数及其图象
17.1 第2课时 自变量的取值范围及函数值
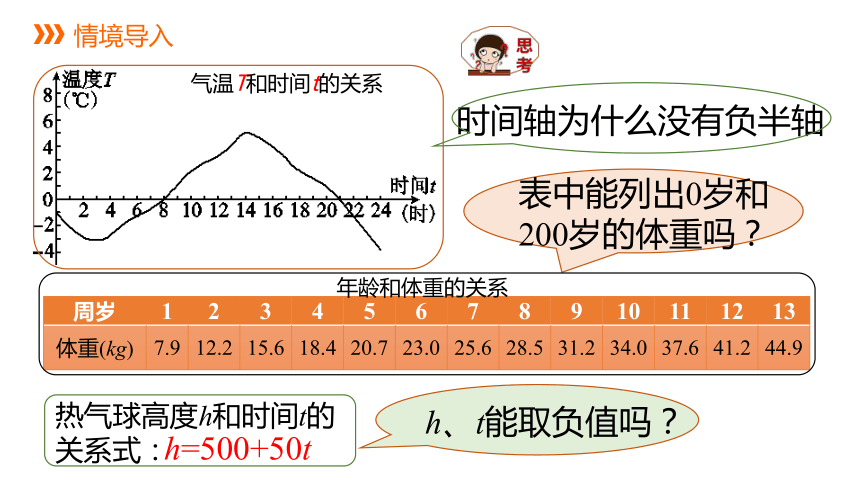
情境导入
周岁 1 2 3 4 5 6 7 8 9 10 11 12 13
体重(kg) 7.9 12.2 15.6 18.4 20.7 23.0 25.6 28.5 31.2 34.0 37.6 41.2 44.9
h=500+50t
热气球高度h和时间t的
关系式:
气温T和时间t的关系
年龄和体重的关系
表中能列出0岁和200岁的体重吗?
h、t能取负值吗?
时间轴为什么没有负半轴
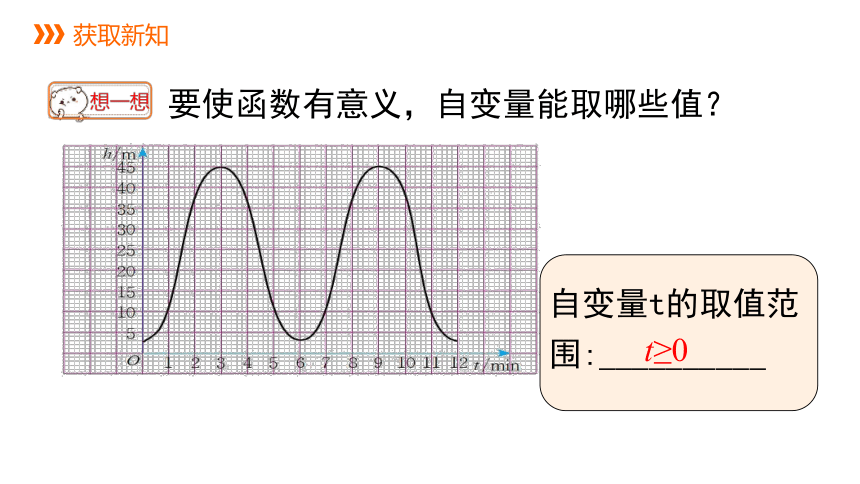
获取新知
要使函数有意义,自变量能取哪些值?
自变量t的取值范围:__________
t≥0
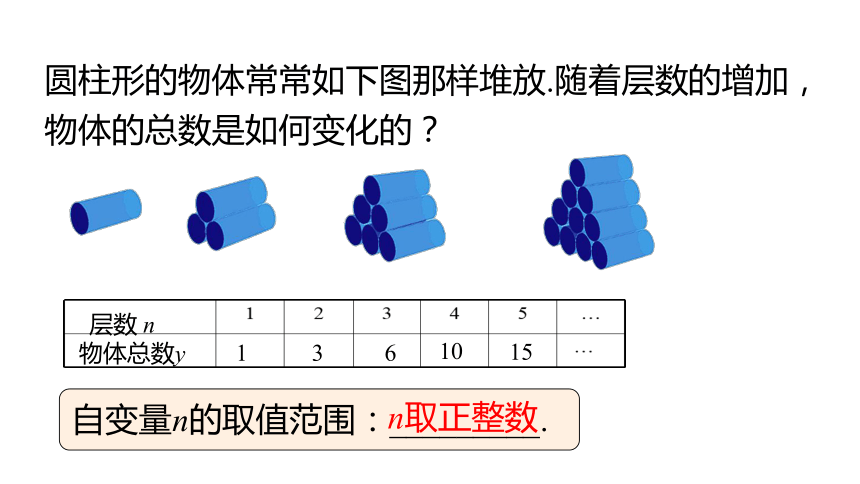
1
3
6
10
15
层数 n
物体总数y
圆柱形的物体常常如下图那样堆放.随着层数的增加,物体的总数是如何变化的?
自变量n的取值范围:_________.
n取正整数
一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
自变量t的取值范围:___________.
t≥-273
你认为函数的自变量可以取任意值吗?
在实际问题中,函数的自变量取值范围往往是有限制的,在限制的范围内,函数才有实际意义;超出这个范围,函数没有实际意义,我们把这种自变量可以取的数值范围叫函数的自变量取值范围.
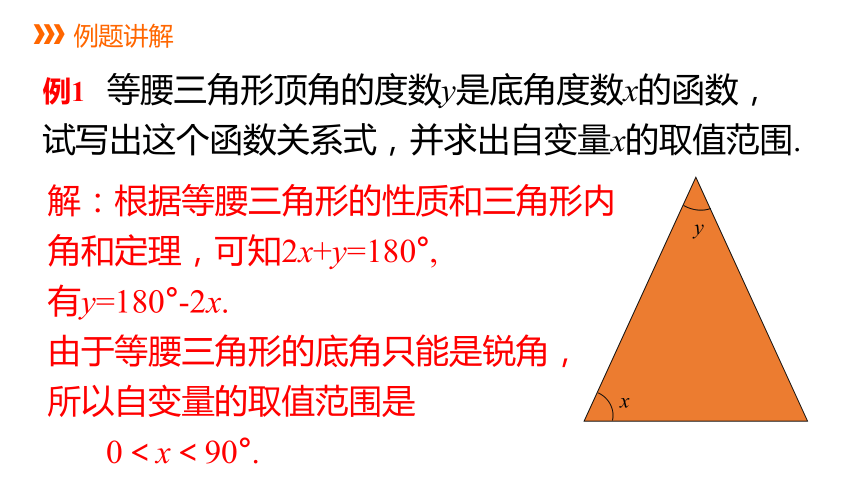
例题讲解
解:根据等腰三角形的性质和三角形内
角和定理,可知2x+y=180°,
有y=180°-2x.
由于等腰三角形的底角只能是锐角,
所以自变量的取值范围是
0<x<90°.
y
x
例1 等腰三角形顶角的度数y是底角度数x的函数,试写出这个函数关系式,并求出自变量x的取值范围.
下列函数中自变量x的取值范围是什么?
-2
x取全体实数
① 函数表达式有意义
求函数自变量的取值范围时,需要考虑:
1.表达式是整式时,自变量取全体实数;
2.表达式是分式时,自变量的取值要使分母不为0;
②符合实际背景
4.表达式是复合式时,自变量的取值是使各式成立的公共解.
3.表达式是偶次根式时,自变量的取值必须使被开方数为非负数.表达式是奇次根式时,自变量取全体实数;
函数值
对于自变量在可取值范围内的一个确定的值a,函数有唯一确定的对应值,这个对应值称为当自变量等于a时的函数值.
即:如果y是x的函数,当x=a时,y=b,那么b叫做当x=a时的函数值.
获取新知
例2 等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,CA与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.
(1)试写出重叠部分面积y cm2与
MA长度x cm之间的函数关系式.
解 :
y与x之间的函数关系式为
例题讲解
(2)当A点向右移动1 cm时,重叠部分的面积是多少
答:MA=1cm时,重叠部分的
面积是 cm2
解 :点A向右移动1 cm,即x=1时.
例3 已知函数
(1)求当x=2,3,-3时,函数的值;
(2)求当x取什么值时,函数的值为0.
解:(1)当x=2时,y= ;
当x=3时,y= ;
当x=-3时,y=7;
把自变量x的值代入关系式中,即可求出函数的值.
(2)令 解得x=
即当x= 时,y=0.
1.函数 y= 中自变量x的取值范围是( )
A.x>2 B.x≥2
C.x≤2 D.x≠2
随堂演练
B
2.已知函数y=2x2-1,当x=2时,函数值y为( )
A.5 B.6
C.7 D.8
C
3.我市白天乘坐出租车收费标准如下:乘坐里程不超过3公里,一律收费8元;超过3公里时,超过3公里的部分,每公里加收1.8元;设乘坐出租车的里程为x(公里)(x为整数),相对应的收费为y(元).
(1)请分别写出当0<x≤3和x>3时,表示y与x的关系式,并直接写出当x=2和x=6时对应的y值;
(2)当0<x≤3和x>3时,y都是x的函数吗?为什么?
解:(1)当0<x≤3时,y=8;
当x>3时,y=8+1.8(x-3)=1.8x+2.6.
当x=2时,y=8;x=6时,y=1.8×6+2.6=13.4.
(2)当0<x≤3和x>3时,y都是x的函数,因为对于x的每一个确定的值,y都有唯一确定的值与其对应.
课堂小结
函数
(1)把自变量的取值代入函数关系式;
(2)计算求值.
①使含自变量的函关系式有数意义;
②涉及实际问题时, 保证实际问题有意义。
函数值
自变量的取值范围
函数关系式
①审清题意; ②找准相等关系;
③选用适当的字母表示自变量和因变量列出相等关系的式子.
第17章 函数及其图象
17.1 第2课时 自变量的取值范围及函数值
情境导入
周岁 1 2 3 4 5 6 7 8 9 10 11 12 13
体重(kg) 7.9 12.2 15.6 18.4 20.7 23.0 25.6 28.5 31.2 34.0 37.6 41.2 44.9
h=500+50t
热气球高度h和时间t的
关系式:
气温T和时间t的关系
年龄和体重的关系
表中能列出0岁和200岁的体重吗?
h、t能取负值吗?
时间轴为什么没有负半轴
获取新知
要使函数有意义,自变量能取哪些值?
自变量t的取值范围:__________
t≥0
1
3
6
10
15
层数 n
物体总数y
圆柱形的物体常常如下图那样堆放.随着层数的增加,物体的总数是如何变化的?
自变量n的取值范围:_________.
n取正整数
一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
自变量t的取值范围:___________.
t≥-273
你认为函数的自变量可以取任意值吗?
在实际问题中,函数的自变量取值范围往往是有限制的,在限制的范围内,函数才有实际意义;超出这个范围,函数没有实际意义,我们把这种自变量可以取的数值范围叫函数的自变量取值范围.
例题讲解
解:根据等腰三角形的性质和三角形内
角和定理,可知2x+y=180°,
有y=180°-2x.
由于等腰三角形的底角只能是锐角,
所以自变量的取值范围是
0<x<90°.
y
x
例1 等腰三角形顶角的度数y是底角度数x的函数,试写出这个函数关系式,并求出自变量x的取值范围.
下列函数中自变量x的取值范围是什么?
-2
x取全体实数
① 函数表达式有意义
求函数自变量的取值范围时,需要考虑:
1.表达式是整式时,自变量取全体实数;
2.表达式是分式时,自变量的取值要使分母不为0;
②符合实际背景
4.表达式是复合式时,自变量的取值是使各式成立的公共解.
3.表达式是偶次根式时,自变量的取值必须使被开方数为非负数.表达式是奇次根式时,自变量取全体实数;
函数值
对于自变量在可取值范围内的一个确定的值a,函数有唯一确定的对应值,这个对应值称为当自变量等于a时的函数值.
即:如果y是x的函数,当x=a时,y=b,那么b叫做当x=a时的函数值.
获取新知
例2 等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,CA与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.
(1)试写出重叠部分面积y cm2与
MA长度x cm之间的函数关系式.
解 :
y与x之间的函数关系式为
例题讲解
(2)当A点向右移动1 cm时,重叠部分的面积是多少
答:MA=1cm时,重叠部分的
面积是 cm2
解 :点A向右移动1 cm,即x=1时.
例3 已知函数
(1)求当x=2,3,-3时,函数的值;
(2)求当x取什么值时,函数的值为0.
解:(1)当x=2时,y= ;
当x=3时,y= ;
当x=-3时,y=7;
把自变量x的值代入关系式中,即可求出函数的值.
(2)令 解得x=
即当x= 时,y=0.
1.函数 y= 中自变量x的取值范围是( )
A.x>2 B.x≥2
C.x≤2 D.x≠2
随堂演练
B
2.已知函数y=2x2-1,当x=2时,函数值y为( )
A.5 B.6
C.7 D.8
C
3.我市白天乘坐出租车收费标准如下:乘坐里程不超过3公里,一律收费8元;超过3公里时,超过3公里的部分,每公里加收1.8元;设乘坐出租车的里程为x(公里)(x为整数),相对应的收费为y(元).
(1)请分别写出当0<x≤3和x>3时,表示y与x的关系式,并直接写出当x=2和x=6时对应的y值;
(2)当0<x≤3和x>3时,y都是x的函数吗?为什么?
解:(1)当0<x≤3时,y=8;
当x>3时,y=8+1.8(x-3)=1.8x+2.6.
当x=2时,y=8;x=6时,y=1.8×6+2.6=13.4.
(2)当0<x≤3和x>3时,y都是x的函数,因为对于x的每一个确定的值,y都有唯一确定的值与其对应.
课堂小结
函数
(1)把自变量的取值代入函数关系式;
(2)计算求值.
①使含自变量的函关系式有数意义;
②涉及实际问题时, 保证实际问题有意义。
函数值
自变量的取值范围
函数关系式
①审清题意; ②找准相等关系;
③选用适当的字母表示自变量和因变量列出相等关系的式子.
