华师大版数学八年级下册同步课件:17.5 第2课时 一次函数与一元一次方程、一元一次不等式(共16张PPT)
文档属性
| 名称 | 华师大版数学八年级下册同步课件:17.5 第2课时 一次函数与一元一次方程、一元一次不等式(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 658.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 11:25:04 | ||
图片预览



文档简介
(共16张PPT)
第17章 函数及其图象
17.5 第2课时 一次函数与一元一次
方程(不等式)
x=-2
x>-2
情景导入
我没看出来!
搞定!
谁能看图象说出一元一次方程的解、一元一次不等式的解集
x+3=0
x+3>0
怎么做到的呢?我们一起探究!
获取新知
画出函数y= x+3的图象,根据图象,说明:
(1)x取什么值时,函数值y等于0?
(2) x取什么值时,函数值y大于0?
x>-2
x=-2
一元一次方程 x+3 =0的解、不等式 x+ 3 > 0的解集与函数y = x+ 3的图象有什么关系?
一元一次方程 x+3 =0的解就是对应一次函数y= x+3函数值为0时,自变量的值;或一次函数y= x+3的图像与x轴交点的横坐标。
不等式 x+ 3 > 0的解集就是对应一次函数y= x+3函数值大于0时,自变量的取值;或一次函数y= x+ 3的图像在x轴上方的点的横坐标。
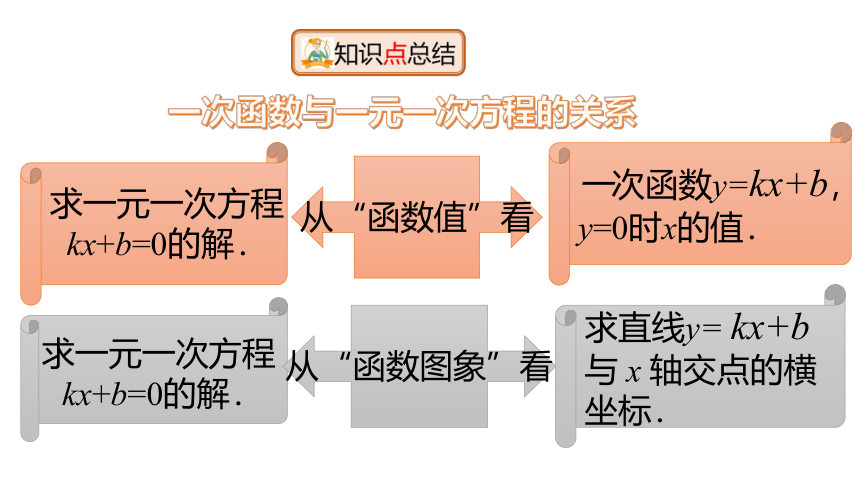
求一元一次方程
kx+b=0的解.
一次函数与一元一次方程的关系
一次函数y=kx+b,
y=0时x的值.
从“函数值”看
求一元一次方程
kx+b=0的解.
求直线y= kx+b
与 x 轴交点的横
坐标.
从“函数图象”看
例题讲解
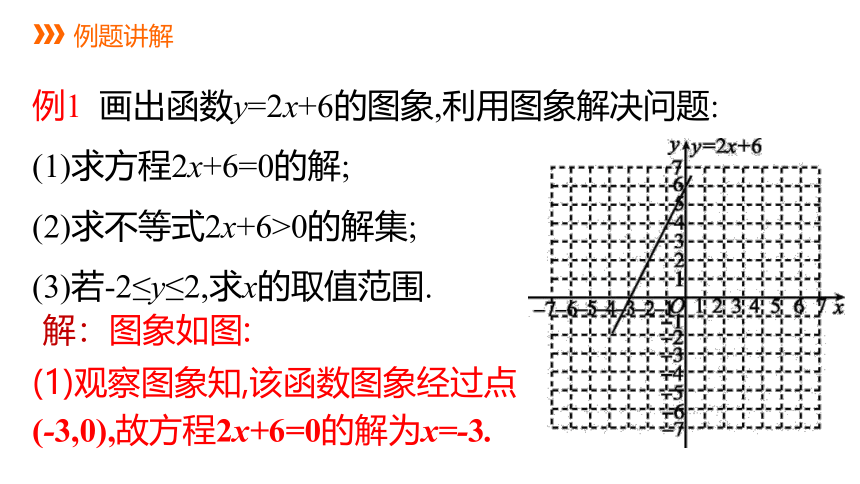
例1 画出函数y=2x+6的图象,利用图象解决问题:
(1)求方程2x+6=0的解;
(2)求不等式2x+6>0的解集;
(3)若-2≤y≤2,求x的取值范围.
解:图象如图:
(1)观察图象知,该函数图象经过点
(-3,0),故方程2x+6=0的解为x=-3.
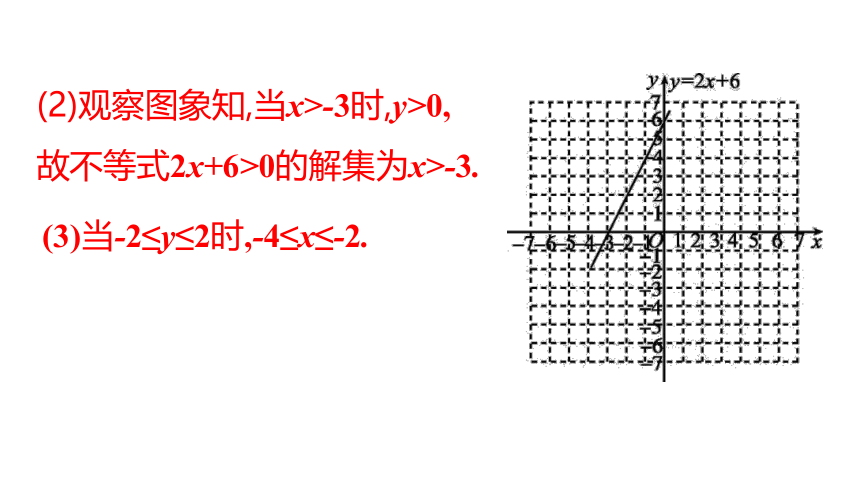
(2)观察图象知,当x>-3时,y>0,
故不等式2x+6>0的解集为x>-3.
(3)当-2≤y≤2时,-4≤x≤-2.
一次函数与一元一次方程、一元一次不等式的关系:
(1)使一次函数y=kx+b的函数值为零的自变量x的值是方程kx+b=0的解;
(2)使一次函数y=kx+b的函数值大于零的自变量的取值范围是不等式kx+b>0的解集;
(3)使一次函数y=kx+b的函数值小于零的自变量的取值范围是不等式kx+b<0的解集.
例2 已知两直线y1=2x-3,y2=6-x.
(1)在同一直角坐标系中作出这两条直线.
(2)求它们的交点A的坐标.
(3)根据图象指出:x为何值时,y1>y2;x为何值时,y1解:(1)如图.
(2)解方程组 得
所以点A的坐标为(3,3).
(3)当x>3时,y1>y2;当x<3时,y11.方程x+1=0的解就是函数y=x+1的图象
与( )
A.x轴交点的横坐标
B.y轴交点的横坐标
C.y轴交点的纵坐标
D.x轴交点的纵坐标
随堂演练
A
2.如图,直线y=ax+b过点A(0,2)和点
B(-3,0),则方程ax+b=0的解是( )
A.x=2
B.x=0
C.x=-1
D.x=-3
D
3.一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为 ( )
A.x=2 B.y=2
C.x=-1 D.y=-1
C
4.如图,直线y1=-x+a与y2=bx-4相交于点P,已知点P的坐标为(1,-3),则关于x的不等式-x+ax >1
5.已知一次函数y1=kx+b与反比例函数y2 的图象如图所示,则当y1>y2时,自变量x满足的条件是 ( )
A. x<-1或0<x<3
B. -1<x<0或x>3
C. -1<x<0
D. x>3
=
A
课堂小结
一次函数与一元一次方程、不等式
解一元一次方程 对应一次函数的值为0时,求相应的自变量的值,即一次函数与x轴交点的横坐标.
解一元一次不等式 对应一次函数的函数值大(小)于0时,求自变量的取值范围,即在x轴上方(或下方)的图象所对应的x取值范围 .
第17章 函数及其图象
17.5 第2课时 一次函数与一元一次
方程(不等式)
x=-2
x>-2
情景导入
我没看出来!
搞定!
谁能看图象说出一元一次方程的解、一元一次不等式的解集
x+3=0
x+3>0
怎么做到的呢?我们一起探究!
获取新知
画出函数y= x+3的图象,根据图象,说明:
(1)x取什么值时,函数值y等于0?
(2) x取什么值时,函数值y大于0?
x>-2
x=-2
一元一次方程 x+3 =0的解、不等式 x+ 3 > 0的解集与函数y = x+ 3的图象有什么关系?
一元一次方程 x+3 =0的解就是对应一次函数y= x+3函数值为0时,自变量的值;或一次函数y= x+3的图像与x轴交点的横坐标。
不等式 x+ 3 > 0的解集就是对应一次函数y= x+3函数值大于0时,自变量的取值;或一次函数y= x+ 3的图像在x轴上方的点的横坐标。
求一元一次方程
kx+b=0的解.
一次函数与一元一次方程的关系
一次函数y=kx+b,
y=0时x的值.
从“函数值”看
求一元一次方程
kx+b=0的解.
求直线y= kx+b
与 x 轴交点的横
坐标.
从“函数图象”看
例题讲解
例1 画出函数y=2x+6的图象,利用图象解决问题:
(1)求方程2x+6=0的解;
(2)求不等式2x+6>0的解集;
(3)若-2≤y≤2,求x的取值范围.
解:图象如图:
(1)观察图象知,该函数图象经过点
(-3,0),故方程2x+6=0的解为x=-3.
(2)观察图象知,当x>-3时,y>0,
故不等式2x+6>0的解集为x>-3.
(3)当-2≤y≤2时,-4≤x≤-2.
一次函数与一元一次方程、一元一次不等式的关系:
(1)使一次函数y=kx+b的函数值为零的自变量x的值是方程kx+b=0的解;
(2)使一次函数y=kx+b的函数值大于零的自变量的取值范围是不等式kx+b>0的解集;
(3)使一次函数y=kx+b的函数值小于零的自变量的取值范围是不等式kx+b<0的解集.
例2 已知两直线y1=2x-3,y2=6-x.
(1)在同一直角坐标系中作出这两条直线.
(2)求它们的交点A的坐标.
(3)根据图象指出:x为何值时,y1>y2;x为何值时,y1
(2)解方程组 得
所以点A的坐标为(3,3).
(3)当x>3时,y1>y2;当x<3时,y1
与( )
A.x轴交点的横坐标
B.y轴交点的横坐标
C.y轴交点的纵坐标
D.x轴交点的纵坐标
随堂演练
A
2.如图,直线y=ax+b过点A(0,2)和点
B(-3,0),则方程ax+b=0的解是( )
A.x=2
B.x=0
C.x=-1
D.x=-3
D
3.一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为 ( )
A.x=2 B.y=2
C.x=-1 D.y=-1
C
4.如图,直线y1=-x+a与y2=bx-4相交于点P,已知点P的坐标为(1,-3),则关于x的不等式-x+a
5.已知一次函数y1=kx+b与反比例函数y2 的图象如图所示,则当y1>y2时,自变量x满足的条件是 ( )
A. x<-1或0<x<3
B. -1<x<0或x>3
C. -1<x<0
D. x>3
=
A
课堂小结
一次函数与一元一次方程、不等式
解一元一次方程 对应一次函数的值为0时,求相应的自变量的值,即一次函数与x轴交点的横坐标.
解一元一次不等式 对应一次函数的函数值大(小)于0时,求自变量的取值范围,即在x轴上方(或下方)的图象所对应的x取值范围 .
