华师大版数学八年级下册同步课件:17.5 第3课时 函数在实际生活中的应用(共13张PPT)
文档属性
| 名称 | 华师大版数学八年级下册同步课件:17.5 第3课时 函数在实际生活中的应用(共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 207.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 16:21:15 | ||
图片预览





文档简介
(共13张PPT)
第17章 函数及其图象
17.5 第3课时 函数在实际生活中的应用
情景导入
t(°C) -40 -20 -10 0 10 20 40 60
V(cm3) 998.3 999.2 999.6 1000 1000.3 1000.7 1001.6 1002.3
为了研究某合金材料的体积V(cm3)随温度t(℃)变化的规律,对一个用这种合金制成的圆球测得相关数据如下:
你能否据此求出V和t的函数关系
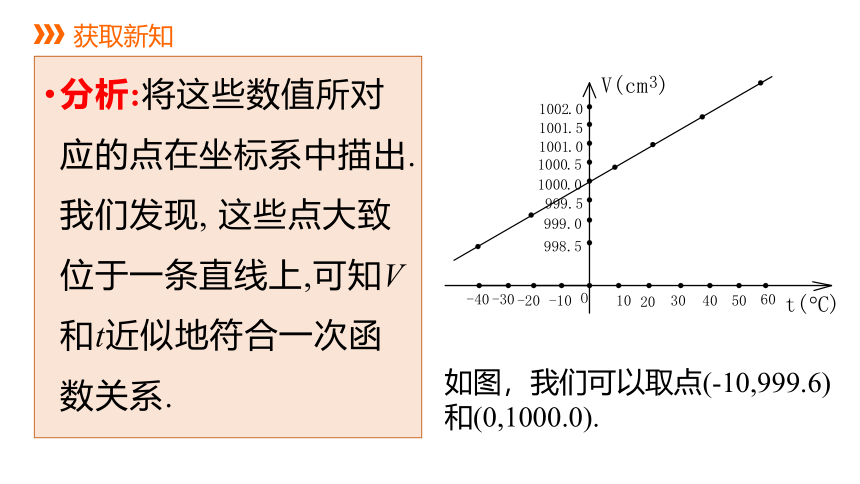
分析:将这些数值所对应的点在坐标系中描出.我们发现, 这些点大致位于一条直线上,可知V和t近似地符合一次函数关系.
如图,我们可以取点(-10,999.6)和(0,1000.0).
获取新知
解:设体积V(cm3)和温度t(°C)之间的函数关系式为V=mt+n(m≠0).由图得,当t= -10时,V=999.6;当t =0时,V=1000.0 则有
解得
故体积V(cm3)和温度(°C)之间的函数关系式近似为V=0.04t+1000.0.
-10m+n= 999.6
n=1000
m=0.04
n=1 000.0
我们曾采用待定系数法求得一次函数和反比例函数的关系式. 但是现实 生活中的数量关系是错综复杂的,在实践中得到一些变量的对应值,有时很难精确地判断它们是什么函数,需要我们根据经验分析,也需要进行近似计算和修正, 建立比较接近的函数关系式进行研究.
常用的方法是:把实践或调查中得到的一些变量的值,通过描点得出函数的近似图象,再根据画出的图象的特征,猜想相应的函数类型,然后利用待定系数法求出函数关系式进而解决实际问题.
例1为了研究某地的气温t(℃)与高度h(千米)之间的关系,某日研究人员在该地的不同高度处同时进行了若干次测量,测得的数据如下表:
(1)在直角坐标系中,作出各组有序数对(h,t)所对应的点;
(2)这些点是否近似在一条直线上
(3)写出t与h之间的一个近似关系式;
(4)估计此时3.5千米高度处的气温.
h/千米 0 0.5 1 1.5 2 2.5 3 …
t/℃ 25 21.8 18.6 15.3 12 8.7 5.5 …
例题讲解
解析:
(1)建立直角坐标系描点;
(2 )观察图象可得;
(3)可设t=kh+b,利用两个点的坐标,可求出关系式;
(4)令h=3.5,求出t即可.
(3)设t与h之间的一个近似关系式为
t=kh+b,把(0,25),(2,12)代入上式,得:
解得:
∴t与h之间的一个近似关系式为
t=-6.5h+25.
(4)当h=3.5时,t=25-6.5×3.5=2.25,
∴此时3.5千米高度处的气温约为2.25 ℃.
解:(1)如图:(2)观察图象可知,这些点近似在一条直线上.
实际问题中的函数关系:
(1)先确定函数的类型;
(2)作出函数的近似图象;
(3)利用函数性质解决相关问题.
随堂演练
1.某快递公司每天上午9:00—10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为 ( )
A.9:15 B.9:20
C.9:25 D.9:30
B
2.草莓营养丰富、味道鲜美.某草莓种植基地今年上半年草莓的月销售量P(千克)与月份x之间的相关数据如下表:
月销售量P(千克)与月份x之间的函数关系式为 (不要求写出自变量的取值范围).
月份x 1月 2月 3月 4月 5月 6月
月销售量P(千克) 4500 5000 5500 6000 6500 7000
P=500x+4000.
课堂小结
求实际问题中的函数关系式
一是找_____________建立函数关系式
相等关系
二是 ,用待定系数法
确定函数关系式
设函数关系式
第17章 函数及其图象
17.5 第3课时 函数在实际生活中的应用
情景导入
t(°C) -40 -20 -10 0 10 20 40 60
V(cm3) 998.3 999.2 999.6 1000 1000.3 1000.7 1001.6 1002.3
为了研究某合金材料的体积V(cm3)随温度t(℃)变化的规律,对一个用这种合金制成的圆球测得相关数据如下:
你能否据此求出V和t的函数关系
分析:将这些数值所对应的点在坐标系中描出.我们发现, 这些点大致位于一条直线上,可知V和t近似地符合一次函数关系.
如图,我们可以取点(-10,999.6)和(0,1000.0).
获取新知
解:设体积V(cm3)和温度t(°C)之间的函数关系式为V=mt+n(m≠0).由图得,当t= -10时,V=999.6;当t =0时,V=1000.0 则有
解得
故体积V(cm3)和温度(°C)之间的函数关系式近似为V=0.04t+1000.0.
-10m+n= 999.6
n=1000
m=0.04
n=1 000.0
我们曾采用待定系数法求得一次函数和反比例函数的关系式. 但是现实 生活中的数量关系是错综复杂的,在实践中得到一些变量的对应值,有时很难精确地判断它们是什么函数,需要我们根据经验分析,也需要进行近似计算和修正, 建立比较接近的函数关系式进行研究.
常用的方法是:把实践或调查中得到的一些变量的值,通过描点得出函数的近似图象,再根据画出的图象的特征,猜想相应的函数类型,然后利用待定系数法求出函数关系式进而解决实际问题.
例1为了研究某地的气温t(℃)与高度h(千米)之间的关系,某日研究人员在该地的不同高度处同时进行了若干次测量,测得的数据如下表:
(1)在直角坐标系中,作出各组有序数对(h,t)所对应的点;
(2)这些点是否近似在一条直线上
(3)写出t与h之间的一个近似关系式;
(4)估计此时3.5千米高度处的气温.
h/千米 0 0.5 1 1.5 2 2.5 3 …
t/℃ 25 21.8 18.6 15.3 12 8.7 5.5 …
例题讲解
解析:
(1)建立直角坐标系描点;
(2 )观察图象可得;
(3)可设t=kh+b,利用两个点的坐标,可求出关系式;
(4)令h=3.5,求出t即可.
(3)设t与h之间的一个近似关系式为
t=kh+b,把(0,25),(2,12)代入上式,得:
解得:
∴t与h之间的一个近似关系式为
t=-6.5h+25.
(4)当h=3.5时,t=25-6.5×3.5=2.25,
∴此时3.5千米高度处的气温约为2.25 ℃.
解:(1)如图:(2)观察图象可知,这些点近似在一条直线上.
实际问题中的函数关系:
(1)先确定函数的类型;
(2)作出函数的近似图象;
(3)利用函数性质解决相关问题.
随堂演练
1.某快递公司每天上午9:00—10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为 ( )
A.9:15 B.9:20
C.9:25 D.9:30
B
2.草莓营养丰富、味道鲜美.某草莓种植基地今年上半年草莓的月销售量P(千克)与月份x之间的相关数据如下表:
月销售量P(千克)与月份x之间的函数关系式为 (不要求写出自变量的取值范围).
月份x 1月 2月 3月 4月 5月 6月
月销售量P(千克) 4500 5000 5500 6000 6500 7000
P=500x+4000.
课堂小结
求实际问题中的函数关系式
一是找_____________建立函数关系式
相等关系
二是 ,用待定系数法
确定函数关系式
设函数关系式
