华师大版数学八年级下册同步课件:18.1 第3课时 综合运用平行四边形的性质(共14张PPT)
文档属性
| 名称 | 华师大版数学八年级下册同步课件:18.1 第3课时 综合运用平行四边形的性质(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 207.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 16:22:31 | ||
图片预览





文档简介
(共14张PPT)
第18章 平行四边形的性质
18.1 第3课时 综合运用平行四边形的性质
知识回顾
前面我们学行四边形的哪些性质?
平行四边形的对边相等.
平行四边形的对角相等.
如何综合利用这些性质解决问题呢?这节课我们一起探讨一下吧.
平行四边形的邻角互补.
平行四边形的对角线互相平分.
平行四边形边、角、对角线的相关计算和证明
例题讲解
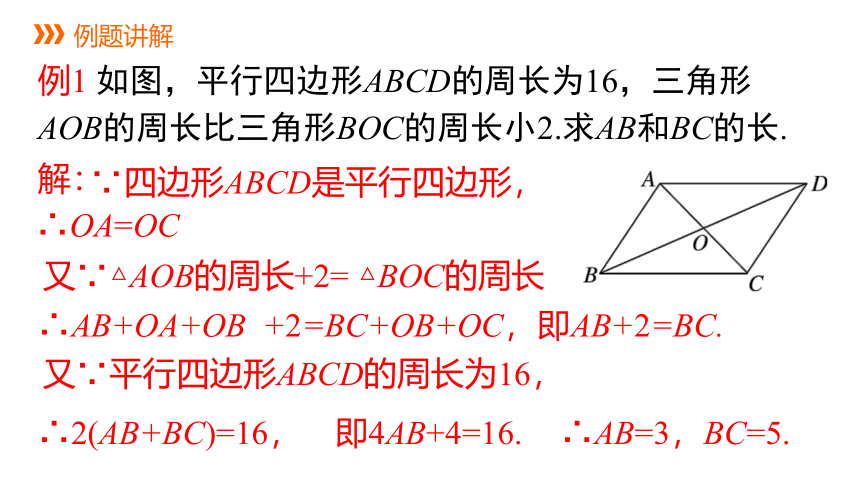
例1 如图,平行四边形ABCD的周长为16,三角形AOB的周长比三角形BOC的周长小2.求AB和BC的长.
解:
∴AB=3,BC=5.
又∵△AOB的周长+2= △BOC的周长
∵四边形ABCD是平行四边形,
∴OA=OC
又∵平行四边形ABCD的周长为16,
∴AB+OA+OB +2=BC+OB+OC,即AB+2=BC.
∴2(AB+BC)=16, 即4AB+4=16.
在应用平行四边形的性质时,我们应从三个方面去考虑:从边、角、对角线看它们的性质;解本例时,我们从“平行四边形的对角线互相平分”中得出“平行四边形被它的两条对角线分成四个小三角形,相邻两个三角形的周长之差等于平行四边形的两邻边之差”,熟记这一结论,能为计算带来很多方便.
平行四边形的有关面积的计算
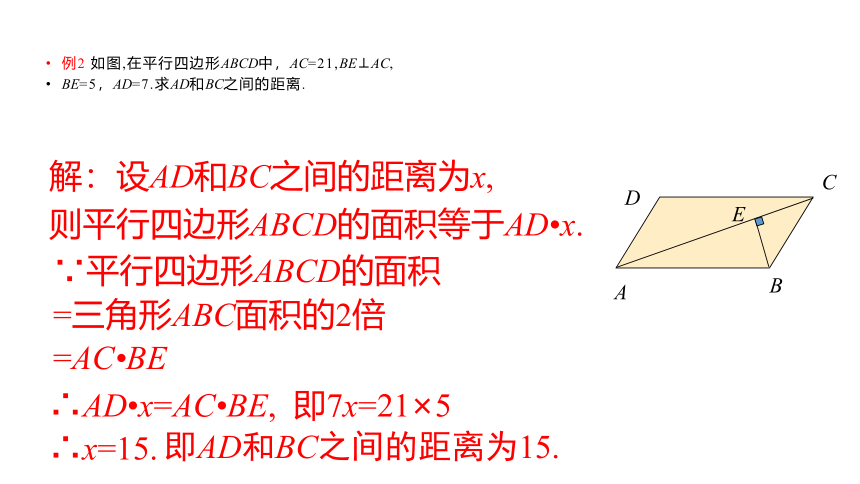
例2 如图,在平行四边形ABCD中,AC=21,BE⊥AC,
BE=5,AD=7.求AD和BC之间的距离.
解:设AD和BC之间的距离为x,
则平行四边形ABCD的面积等于AD x.
∵平行四边形ABCD的面积
=三角形ABC面积的2倍
=AC BE
∴AD x=AC BE, 即7x=21×5
∴x=15.
即AD和BC之间的距离为15.
A
B
C
D
E
1. 如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB长为( )
A.8 B.10 C.6 D.4
D
随堂演练
2.如图,在 ABCD中,CE⊥AB,E为垂足,如果∠A=120°,那么∠BCE的度数是( )
A.80°
B.50°
C.40°
D.30°
D
3.如图,在梯形ABCD中,AD∥BC,记△ABO的面积为S1,△COD的面积为S2,则S1,S2的大小关系是( )
A.S1>S2 B.S1=S2
C.S1<S2 D.无法比较
B
C
4.如图,已知 ABCD的对角线AC与BD相交于点O,AB⊥AC. 若AB=4,AC=6,则BD的长是( )
A.8
B.9
C.10
D.11
5.如图,若 ABCD的周长为36 cm,过点D分别作AB,BC边上的高DE,DF,且DE=4 cm,DF=5 cm, ABCD的面积为( )cm2.
A.40 B.32 C.36 D.50
A
6. 如图,已知 ABCD与 EBFD的顶点A,E,F,C在一条直线上,求证:AE=CF.
证明:如图,连接BD交AC于点O.
∵四边形ABCD是平行四边形,
∴OA=OC
∵四边形EBFD是平行四边形,
∴OE=OF
∴OA-OE=OC-OF,即AE=CF .
课堂小结
平行四边形性质综合应用
平行四边形边、对角线的相关计算和证明
平行四边形的有关面积计算
第18章 平行四边形的性质
18.1 第3课时 综合运用平行四边形的性质
知识回顾
前面我们学行四边形的哪些性质?
平行四边形的对边相等.
平行四边形的对角相等.
如何综合利用这些性质解决问题呢?这节课我们一起探讨一下吧.
平行四边形的邻角互补.
平行四边形的对角线互相平分.
平行四边形边、角、对角线的相关计算和证明
例题讲解
例1 如图,平行四边形ABCD的周长为16,三角形AOB的周长比三角形BOC的周长小2.求AB和BC的长.
解:
∴AB=3,BC=5.
又∵△AOB的周长+2= △BOC的周长
∵四边形ABCD是平行四边形,
∴OA=OC
又∵平行四边形ABCD的周长为16,
∴AB+OA+OB +2=BC+OB+OC,即AB+2=BC.
∴2(AB+BC)=16, 即4AB+4=16.
在应用平行四边形的性质时,我们应从三个方面去考虑:从边、角、对角线看它们的性质;解本例时,我们从“平行四边形的对角线互相平分”中得出“平行四边形被它的两条对角线分成四个小三角形,相邻两个三角形的周长之差等于平行四边形的两邻边之差”,熟记这一结论,能为计算带来很多方便.
平行四边形的有关面积的计算
例2 如图,在平行四边形ABCD中,AC=21,BE⊥AC,
BE=5,AD=7.求AD和BC之间的距离.
解:设AD和BC之间的距离为x,
则平行四边形ABCD的面积等于AD x.
∵平行四边形ABCD的面积
=三角形ABC面积的2倍
=AC BE
∴AD x=AC BE, 即7x=21×5
∴x=15.
即AD和BC之间的距离为15.
A
B
C
D
E
1. 如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB长为( )
A.8 B.10 C.6 D.4
D
随堂演练
2.如图,在 ABCD中,CE⊥AB,E为垂足,如果∠A=120°,那么∠BCE的度数是( )
A.80°
B.50°
C.40°
D.30°
D
3.如图,在梯形ABCD中,AD∥BC,记△ABO的面积为S1,△COD的面积为S2,则S1,S2的大小关系是( )
A.S1>S2 B.S1=S2
C.S1<S2 D.无法比较
B
C
4.如图,已知 ABCD的对角线AC与BD相交于点O,AB⊥AC. 若AB=4,AC=6,则BD的长是( )
A.8
B.9
C.10
D.11
5.如图,若 ABCD的周长为36 cm,过点D分别作AB,BC边上的高DE,DF,且DE=4 cm,DF=5 cm, ABCD的面积为( )cm2.
A.40 B.32 C.36 D.50
A
6. 如图,已知 ABCD与 EBFD的顶点A,E,F,C在一条直线上,求证:AE=CF.
证明:如图,连接BD交AC于点O.
∵四边形ABCD是平行四边形,
∴OA=OC
∵四边形EBFD是平行四边形,
∴OE=OF
∴OA-OE=OC-OF,即AE=CF .
课堂小结
平行四边形性质综合应用
平行四边形边、对角线的相关计算和证明
平行四边形的有关面积计算
