华师大版数学八年级下册同步课件:18.2 第3课时 平行四边形的判定与性质的综合应用(共16张PPT)
文档属性
| 名称 | 华师大版数学八年级下册同步课件:18.2 第3课时 平行四边形的判定与性质的综合应用(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 164.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
第18章 平行四边形的性质
18.2 第3课时 平行四边形的判定与性质的综合应用
知识回顾
关于平行四边形你知道多少?
它的判定方法有哪些?
1.两组对边分别相等
2.两组对角分别相等
3.两条对角线互相平分
1.两组对边分别相等的四边形是平行四边形
2.一组对边平行且相等的四边形是平行四边形
3.对角线互相平分的四边形是平行四边形
它有哪些主要性质呢?
A
B
C
D
E
F
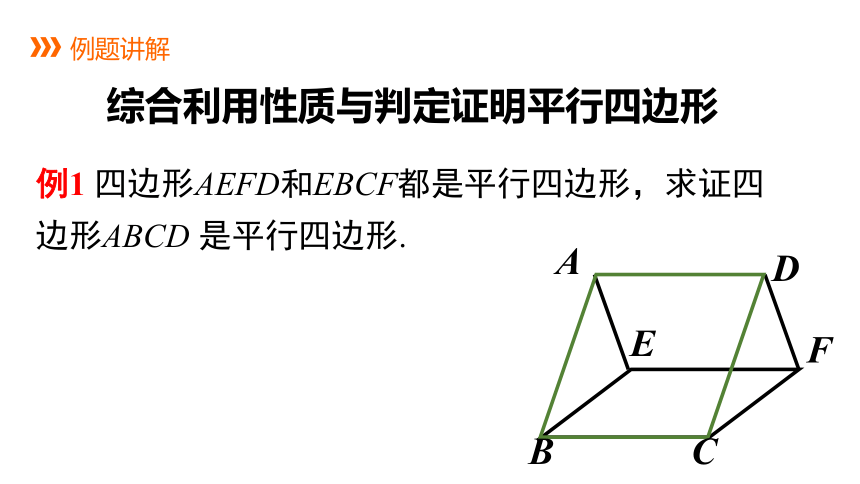
例1 四边形AEFD和EBCF都是平行四边形,求证四边形ABCD 是平行四边形.
综合利用性质与判定证明平行四边形
例题讲解
A
B
C
D
E
F
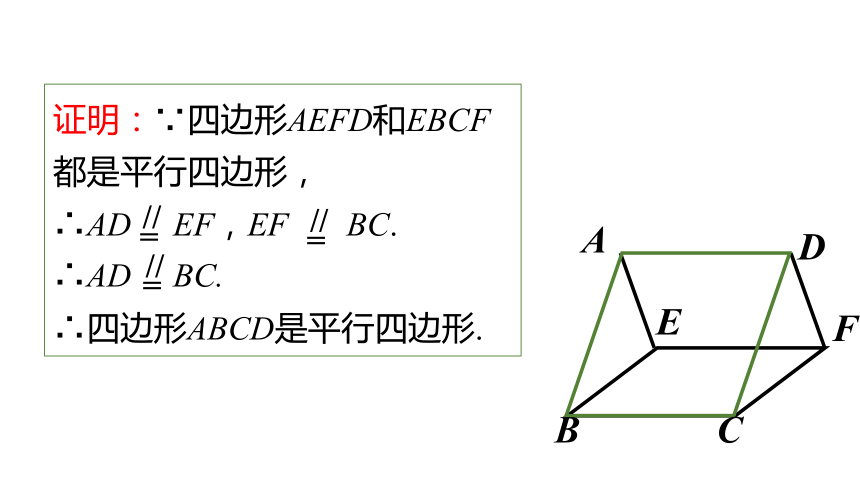
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD EF,EF BC.
∴AD BC.
∴四边形ABCD是平行四边形.
//
=
//
=
//
=
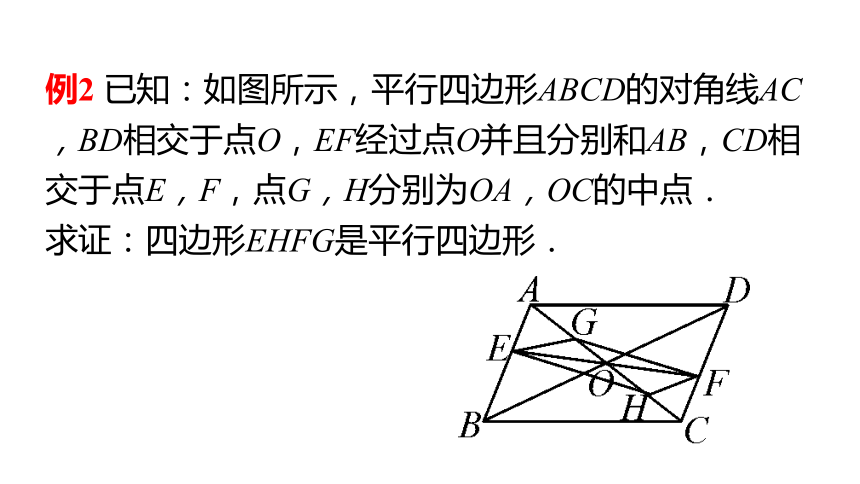
例2 已知:如图所示,平行四边形ABCD的对角线AC,BD相交于点O,EF经过点O并且分别和AB,CD相交于点E,F,点G,H分别为OA,OC的中点.
求证:四边形EHFG是平行四边形.
证明:如图所示,
∵点O为平行四边形ABCD对角线AC,BD的交点,
∴OA=OC,OB=OD.
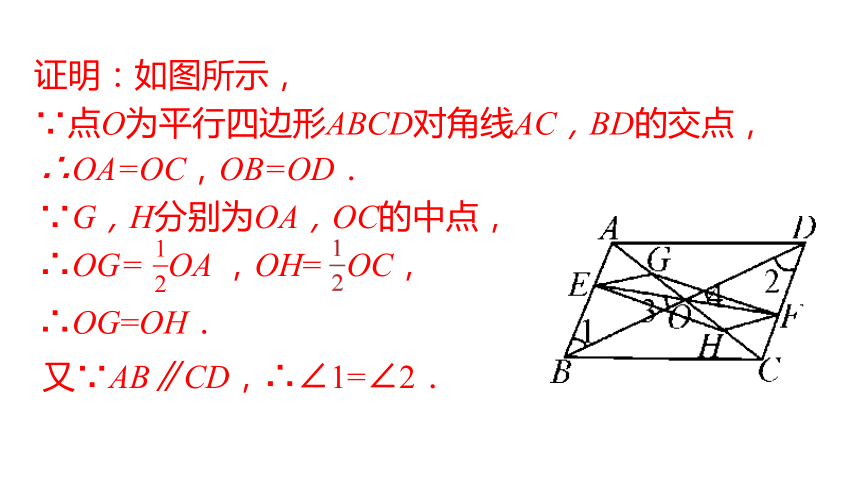
∵G,H分别为OA,OC的中点,
∴OG= OA ,OH= OC,
又∵AB∥CD,∴∠1=∠2.
∴OG=OH.
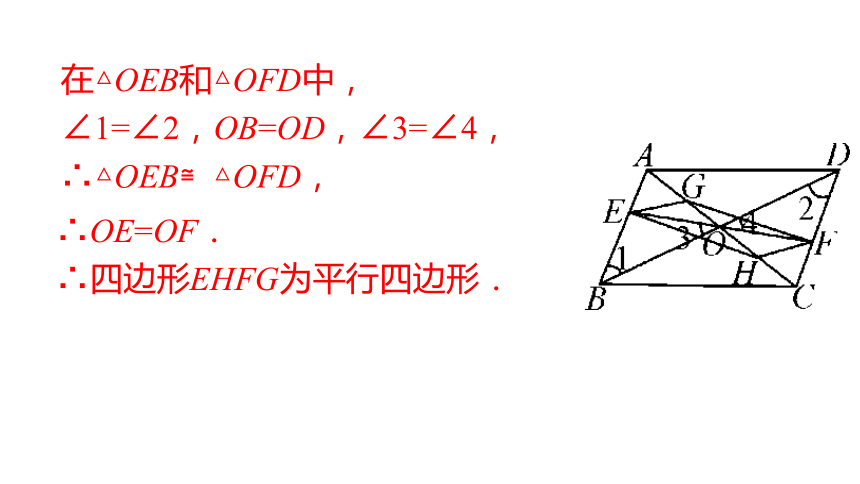
在△OEB和△OFD中,
∠1=∠2,OB=OD,∠3=∠4,
∴△OEB≌△OFD,
∴OE=OF.
∴四边形EHFG为平行四边形.
例3 如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.
(1)求证:△ABD≌△CAE;
(2)连结ED,线段DE与AB之间有怎样的位置和数量关系?请说明理由.
利用性质与判定探究线段、角的关系
(1)证明:∵AB=AC,AD是BC边上的中线,
∴AD⊥BC.
∵AE∥BC,CE⊥AE,∴AD=EC.
又∵AB=CA,
∴△ABD≌△CAE(H.L).
(2)解:DE∥AB且DE=AB.理由如下:
∵△ABD≌△CAE,∴AE=BD.
又∵AE∥BD,
∴四边形ABDE是平行四边形.
∴DE∥AB且DE=AB.
随堂演练
1.如图, ABCD中,E,F分别为AD,BC边上的点,要使四边形BEDF为平行四边形,需添加一个条件:
______________________________________________.
AE=FC或∠ABE=∠CDF或BE∥DF(答案不唯一)
2.如图,在 ABCD中,E,F分别是AB,CD的中点.
(1)求证:四边形EBFD为平行四边形;
(2)对角线AC分别与DE,BF交于点M,N,求证:
△ABN≌△CDM.
(1)∵四边形ABCD为平行四边形,
∴AB=CD,EB∥DF.
又∵E,F分别是AB,CD的中点,
∴EB= AB,DF= CD.
∴EB=DF. ∴四边形EBFD为平行四边形.
证明:
(2)∵四边形EBFD为平行四边形,
∴∠ABN=∠CDM.
∵AB∥CD,∴∠BAN=∠DCM.
又∵AB=CD,∴△ABN≌△CDM.
3.如图,在△ABC中,AB=AC,DE∥BA交AC于E,DF∥CA交AB于F,连接EF,AD,那么是否有下列结论?说明理由.
(1)AD与EF互相平分;(2)AE=BF.
解:
结论(1)(2)都成立,理由如下:
(1)∵DE∥AB,DF∥AC,
∴四边形AFDE是平行四边形.
∴AD与EF互相平分.
(2)在 AFDE中,AE=DF,
∵AC∥DF,
∴∠C=∠FDB.
∵AB=AC,
∴∠C=∠B,
∴∠B=∠FDB,
∴BF=DF=AE,即AE=BF.
解:
课堂小结
平行四边形的性质
判定
得出
四边形是平行四边形
第18章 平行四边形的性质
18.2 第3课时 平行四边形的判定与性质的综合应用
知识回顾
关于平行四边形你知道多少?
它的判定方法有哪些?
1.两组对边分别相等
2.两组对角分别相等
3.两条对角线互相平分
1.两组对边分别相等的四边形是平行四边形
2.一组对边平行且相等的四边形是平行四边形
3.对角线互相平分的四边形是平行四边形
它有哪些主要性质呢?
A
B
C
D
E
F
例1 四边形AEFD和EBCF都是平行四边形,求证四边形ABCD 是平行四边形.
综合利用性质与判定证明平行四边形
例题讲解
A
B
C
D
E
F
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD EF,EF BC.
∴AD BC.
∴四边形ABCD是平行四边形.
//
=
//
=
//
=
例2 已知:如图所示,平行四边形ABCD的对角线AC,BD相交于点O,EF经过点O并且分别和AB,CD相交于点E,F,点G,H分别为OA,OC的中点.
求证:四边形EHFG是平行四边形.
证明:如图所示,
∵点O为平行四边形ABCD对角线AC,BD的交点,
∴OA=OC,OB=OD.
∵G,H分别为OA,OC的中点,
∴OG= OA ,OH= OC,
又∵AB∥CD,∴∠1=∠2.
∴OG=OH.
在△OEB和△OFD中,
∠1=∠2,OB=OD,∠3=∠4,
∴△OEB≌△OFD,
∴OE=OF.
∴四边形EHFG为平行四边形.
例3 如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.
(1)求证:△ABD≌△CAE;
(2)连结ED,线段DE与AB之间有怎样的位置和数量关系?请说明理由.
利用性质与判定探究线段、角的关系
(1)证明:∵AB=AC,AD是BC边上的中线,
∴AD⊥BC.
∵AE∥BC,CE⊥AE,∴AD=EC.
又∵AB=CA,
∴△ABD≌△CAE(H.L).
(2)解:DE∥AB且DE=AB.理由如下:
∵△ABD≌△CAE,∴AE=BD.
又∵AE∥BD,
∴四边形ABDE是平行四边形.
∴DE∥AB且DE=AB.
随堂演练
1.如图, ABCD中,E,F分别为AD,BC边上的点,要使四边形BEDF为平行四边形,需添加一个条件:
______________________________________________.
AE=FC或∠ABE=∠CDF或BE∥DF(答案不唯一)
2.如图,在 ABCD中,E,F分别是AB,CD的中点.
(1)求证:四边形EBFD为平行四边形;
(2)对角线AC分别与DE,BF交于点M,N,求证:
△ABN≌△CDM.
(1)∵四边形ABCD为平行四边形,
∴AB=CD,EB∥DF.
又∵E,F分别是AB,CD的中点,
∴EB= AB,DF= CD.
∴EB=DF. ∴四边形EBFD为平行四边形.
证明:
(2)∵四边形EBFD为平行四边形,
∴∠ABN=∠CDM.
∵AB∥CD,∴∠BAN=∠DCM.
又∵AB=CD,∴△ABN≌△CDM.
3.如图,在△ABC中,AB=AC,DE∥BA交AC于E,DF∥CA交AB于F,连接EF,AD,那么是否有下列结论?说明理由.
(1)AD与EF互相平分;(2)AE=BF.
解:
结论(1)(2)都成立,理由如下:
(1)∵DE∥AB,DF∥AC,
∴四边形AFDE是平行四边形.
∴AD与EF互相平分.
(2)在 AFDE中,AE=DF,
∵AC∥DF,
∴∠C=∠FDB.
∵AB=AC,
∴∠C=∠B,
∴∠B=∠FDB,
∴BF=DF=AE,即AE=BF.
解:
课堂小结
平行四边形的性质
判定
得出
四边形是平行四边形
