华师大版数学八年级下册同步课件:18.2 第1课时 从边判定平行四边形(共22张PPT)
文档属性
| 名称 | 华师大版数学八年级下册同步课件:18.2 第1课时 从边判定平行四边形(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 335.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
第18章 平行四边形的性质
18.2 第1课时 从边判定平行四边形
一装潢店要招聘店员,老板出了这样一道考题:“一顾客要一张平行四边形的玻璃,你利用工具度量哪些数据可说明这张玻璃符合顾客要求.”
情景导入
你能帮助他回答这个问题吗?
度量哪些数据?
两组对边的长度是否相等。
能说出理由吗?
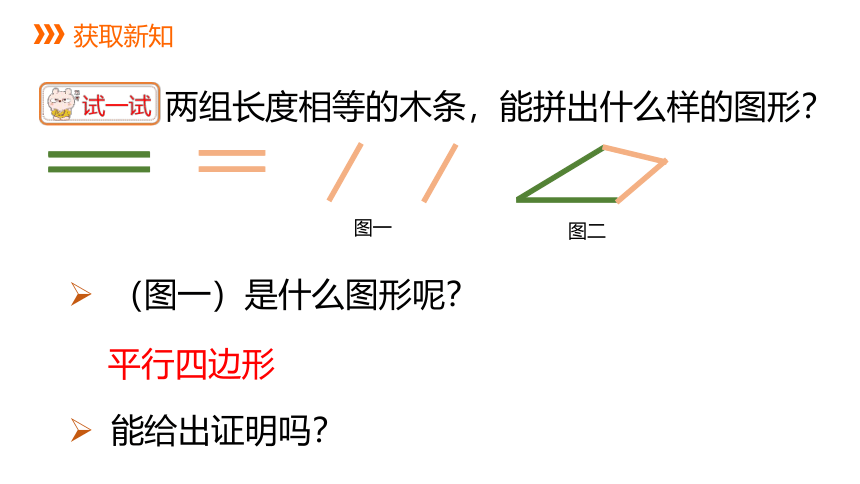
两组长度相等的木条,能拼出什么样的图形?
图一
图二
(图一)是什么图形呢?
能给出证明吗?
平行四边形
获取新知
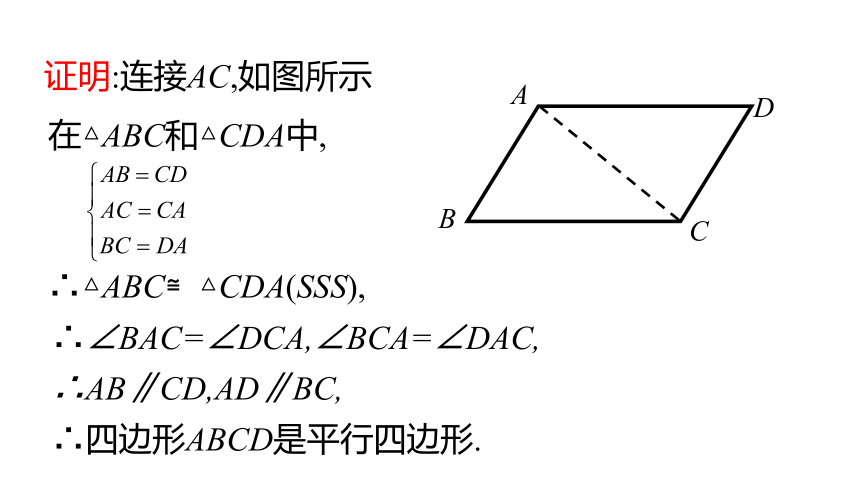
在△ABC和△CDA中,
∴△ABC≌△CDA(SSS),
B
D
C
A
证明:连接AC,如图所示
∴∠BAC=∠DCA,∠BCA=∠DAC,
∴AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
∵AB=CD,
AD=BC
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理1
B
D
C
A
归纳总结
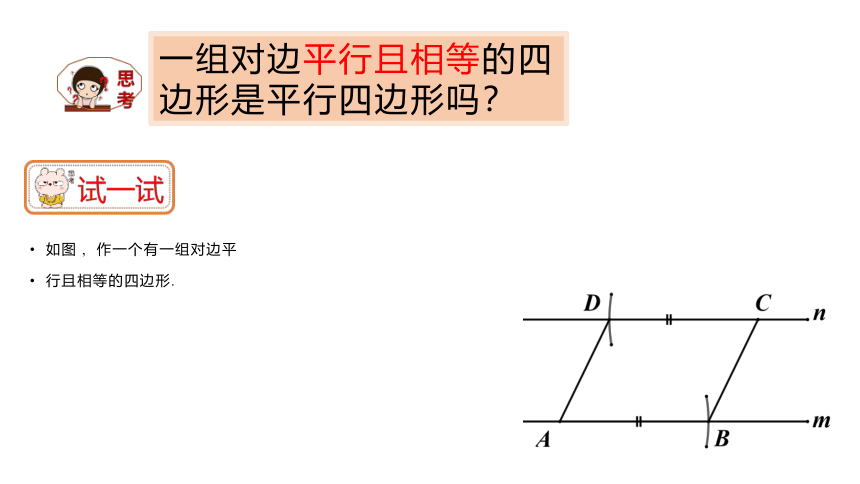
一组对边平行且相等的四边形是平行四边形吗?
如图 , 作一个有一组对边平
行且相等的四边形.
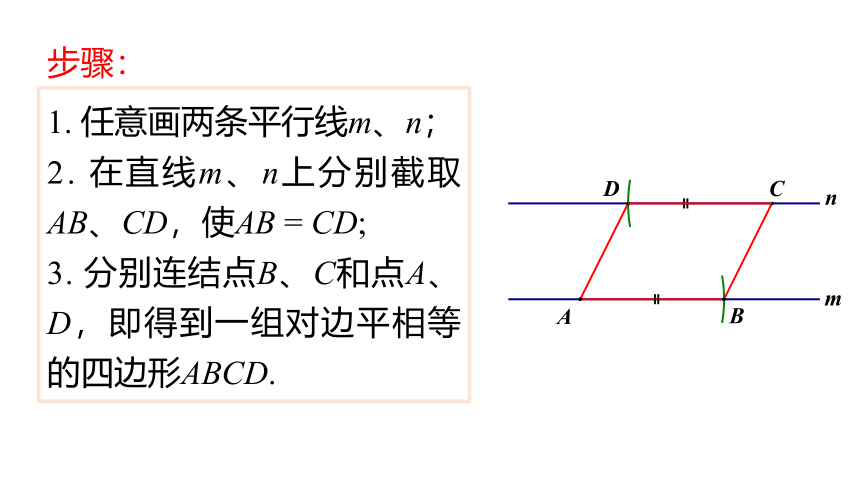
1. 任意画两条平行线m、n;
2. 在直线m、n上分别截取AB、CD,使AB = CD;
3. 分别连结点B、C和点A、D,即得到一组对边平相等的四边形ABCD.
步骤:
m
n
A
B
C
D
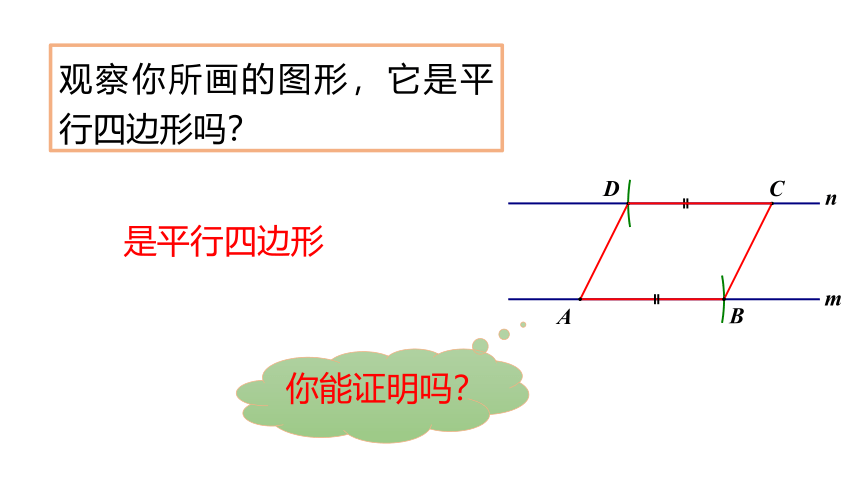
观察你所画的图形,它是平行四边形吗?
是平行四边形
你能证明吗?
m
n
A
B
C
D
已知:如图,在四边形ABCD中,AB=CD且AB∥CD,求证:四边形ABCD是平行四边形.
证明:连接AC.
∵AB∥CD, ∴∠1=∠2.
在△ABC和△CDA中,
AB=CD,
AC=CA,
∠1=∠2,
∴△ABC≌△CDA(SAS),
∴BC=DA .
又∵AB= CD,
∴四边形ABCD是平行四边形.
A
B
C
D
2
1
数学表达式:
∵AB CD,
∴四边形ABCD是平行四边形
一组对边平行且相等的四边形是平行四边形.
平行四边形判定定理2
B
D
C
A
归纳总结
与边有关的判定平行四边形的方法:
1.两组对边分别平行的四边形是平行四边形.
2.两组对边分别相等的四边形是平行四边形.
3.一组对边平行且相等的四边形是平行四边形.
例1 如图,在 ABCD中,点E,F分别在对边BC和DA上,且AF=CE.求证:四边形AECF是平行四边形.
证明:
∵四边形ABCD是平行四边形,
∴BC //AD(平行四边形的对边平行).
即AF∥CE,
又∵ AF =CE.
∴四边形AECF是平行四边形.
例题讲解
如图,分别以△ABC的三边为一边,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.
求证:四边形ADEF是平行四边形.
例2
分析:已知条件中暗含相等的线段,应考虑根据两组对边分别相等的四边形是平行四边形进行判定。
∵△ABD,△BCE,△ACF都为等边三角形,
∴DB=AB=AD,BE=BC,AC=AF,
∠DBA=60°,∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA.
∴∠DBE=∠ABC. ∴△DBE≌△ABC.
∴DE=AC.
又∵AC=AF,∴AF=DE. 同理可证:△ABC≌△FEC,
∴AB=FE. ∴FE=AD.
∴四边形ADEF是平行四边形.
证明:
根据等边三角形的性质可以得到线段相等,角
相等,进而通过证明三角形全等得到四边形ADEF
的两组对边分别相等,根据两组对边分别相等的四
边形是平行四边形得证.
随堂演练
1.如图,在 ABCD中,EF∥AD,HN∥AB,则图中的平行四边形共有( )
A.12个 B.9个
C.7个 D.5个
B
2.下列条件中,能判定四边形ABCD是平行四边形的是 ( )
A.AB=CD,AD=BC
B.AB=AD,CD=BC
C.AB=BC=CD
D.AB=AD,∠B=∠D
A
3.不能判定一个四边形是平行四边形的条件是 ( )
A.两组对边分别平行
B.一组对边平行另一组对边相等
C.一组对边平行且相等
D.两组对边分别相等
B
4.如图, AD⊥AC,BC⊥AC,且AB=CD,求证:四边形ABCD是平行四边形.
证明:在Rt△ABC和Rt△CDA中,
∵AC=CA,AB=CD,
∴Rt△ABC≌Rt△CDA(HL),
∴BC=AD.
又∵AB=CD,
∴四边形ABCD是平行四边形.
5.如图,在四边形ABCD中,AB=CD,过点A作AE⊥BD交BD于点E,过点C作CF⊥BD交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.
证明:∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°.
在Rt△ABE和Rt△CDF中,
∴Rt△ABE≌Rt△CDF,
∴∠ABE=∠CDF,
∴AB∥CD.
∵AB=CD,
∴四边形ABCD是平行四边形.
AB=CD
AE=CF
课堂小结
从边判定平行四边形
判定定理1
判定定理2
两组对边分别相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
第18章 平行四边形的性质
18.2 第1课时 从边判定平行四边形
一装潢店要招聘店员,老板出了这样一道考题:“一顾客要一张平行四边形的玻璃,你利用工具度量哪些数据可说明这张玻璃符合顾客要求.”
情景导入
你能帮助他回答这个问题吗?
度量哪些数据?
两组对边的长度是否相等。
能说出理由吗?
两组长度相等的木条,能拼出什么样的图形?
图一
图二
(图一)是什么图形呢?
能给出证明吗?
平行四边形
获取新知
在△ABC和△CDA中,
∴△ABC≌△CDA(SSS),
B
D
C
A
证明:连接AC,如图所示
∴∠BAC=∠DCA,∠BCA=∠DAC,
∴AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
∵AB=CD,
AD=BC
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理1
B
D
C
A
归纳总结
一组对边平行且相等的四边形是平行四边形吗?
如图 , 作一个有一组对边平
行且相等的四边形.
1. 任意画两条平行线m、n;
2. 在直线m、n上分别截取AB、CD,使AB = CD;
3. 分别连结点B、C和点A、D,即得到一组对边平相等的四边形ABCD.
步骤:
m
n
A
B
C
D
观察你所画的图形,它是平行四边形吗?
是平行四边形
你能证明吗?
m
n
A
B
C
D
已知:如图,在四边形ABCD中,AB=CD且AB∥CD,求证:四边形ABCD是平行四边形.
证明:连接AC.
∵AB∥CD, ∴∠1=∠2.
在△ABC和△CDA中,
AB=CD,
AC=CA,
∠1=∠2,
∴△ABC≌△CDA(SAS),
∴BC=DA .
又∵AB= CD,
∴四边形ABCD是平行四边形.
A
B
C
D
2
1
数学表达式:
∵AB CD,
∴四边形ABCD是平行四边形
一组对边平行且相等的四边形是平行四边形.
平行四边形判定定理2
B
D
C
A
归纳总结
与边有关的判定平行四边形的方法:
1.两组对边分别平行的四边形是平行四边形.
2.两组对边分别相等的四边形是平行四边形.
3.一组对边平行且相等的四边形是平行四边形.
例1 如图,在 ABCD中,点E,F分别在对边BC和DA上,且AF=CE.求证:四边形AECF是平行四边形.
证明:
∵四边形ABCD是平行四边形,
∴BC //AD(平行四边形的对边平行).
即AF∥CE,
又∵ AF =CE.
∴四边形AECF是平行四边形.
例题讲解
如图,分别以△ABC的三边为一边,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.
求证:四边形ADEF是平行四边形.
例2
分析:已知条件中暗含相等的线段,应考虑根据两组对边分别相等的四边形是平行四边形进行判定。
∵△ABD,△BCE,△ACF都为等边三角形,
∴DB=AB=AD,BE=BC,AC=AF,
∠DBA=60°,∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA.
∴∠DBE=∠ABC. ∴△DBE≌△ABC.
∴DE=AC.
又∵AC=AF,∴AF=DE. 同理可证:△ABC≌△FEC,
∴AB=FE. ∴FE=AD.
∴四边形ADEF是平行四边形.
证明:
根据等边三角形的性质可以得到线段相等,角
相等,进而通过证明三角形全等得到四边形ADEF
的两组对边分别相等,根据两组对边分别相等的四
边形是平行四边形得证.
随堂演练
1.如图,在 ABCD中,EF∥AD,HN∥AB,则图中的平行四边形共有( )
A.12个 B.9个
C.7个 D.5个
B
2.下列条件中,能判定四边形ABCD是平行四边形的是 ( )
A.AB=CD,AD=BC
B.AB=AD,CD=BC
C.AB=BC=CD
D.AB=AD,∠B=∠D
A
3.不能判定一个四边形是平行四边形的条件是 ( )
A.两组对边分别平行
B.一组对边平行另一组对边相等
C.一组对边平行且相等
D.两组对边分别相等
B
4.如图, AD⊥AC,BC⊥AC,且AB=CD,求证:四边形ABCD是平行四边形.
证明:在Rt△ABC和Rt△CDA中,
∵AC=CA,AB=CD,
∴Rt△ABC≌Rt△CDA(HL),
∴BC=AD.
又∵AB=CD,
∴四边形ABCD是平行四边形.
5.如图,在四边形ABCD中,AB=CD,过点A作AE⊥BD交BD于点E,过点C作CF⊥BD交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.
证明:∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°.
在Rt△ABE和Rt△CDF中,
∴Rt△ABE≌Rt△CDF,
∴∠ABE=∠CDF,
∴AB∥CD.
∵AB=CD,
∴四边形ABCD是平行四边形.
AB=CD
AE=CF
课堂小结
从边判定平行四边形
判定定理1
判定定理2
两组对边分别相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
