华师大版数学八年级下册同步课件:19.2.1 第1课时 菱形的性质(共19张PPT)
文档属性
| 名称 | 华师大版数学八年级下册同步课件:19.2.1 第1课时 菱形的性质(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 323.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
第19章 矩形、菱形和正方形
19.2.1 第1课时 菱形的性质
情景导入
将一张矩形的纸对折,再对折,
然后沿着图中的虚线剪下,打开,
你发现这是一个什么样的图形?
对边相等吗?是什么图形?
邻边相等吗?是什么图形?
平行四边形
答案马上揭晓!
相等
相等
获取新知
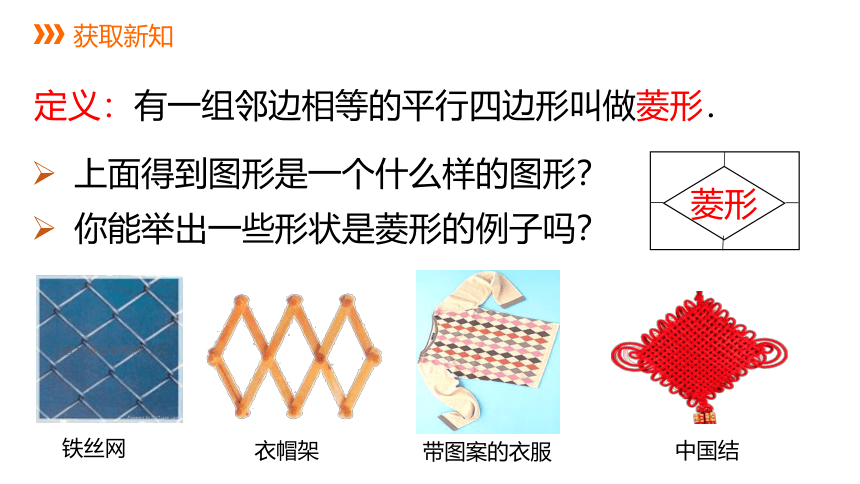
定义:有一组邻边相等的平行四边形叫做菱形.
上面得到图形是一个什么样的图形?
菱形
你能举出一些形状是菱形的例子吗?
铁丝网
衣帽架
带图案的衣服
中国结
(1)菱形必须满足两个条件:一是平行四边形; 二是一组邻边相等.二者必须同时具备,缺一不可;
(2)菱形的定义既是菱形的基本性质,也是菱形的基本判定方法.
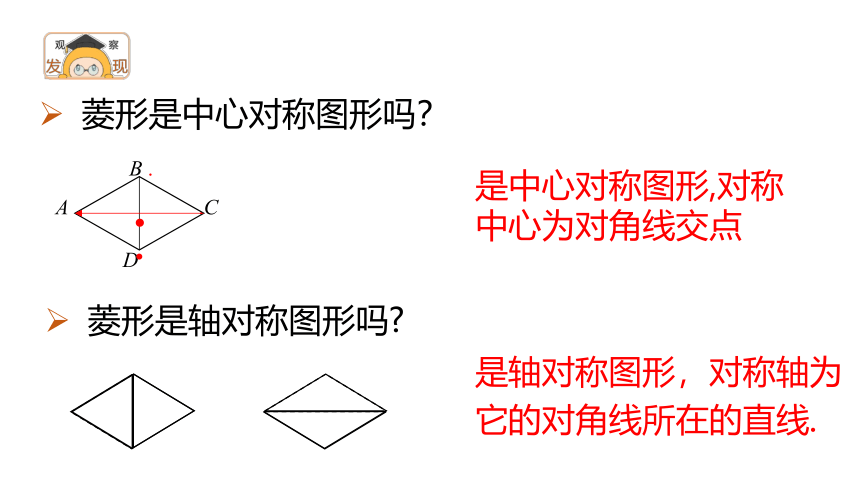
菱形是轴对称图形吗
菱形是中心对称图形吗?
.C
D
B .
A .
.
是中心对称图形,对称中心为对角线交点
.
是轴对称图形,对称轴为它的对角线所在的直线.
.C
D
B .
A .
.
.
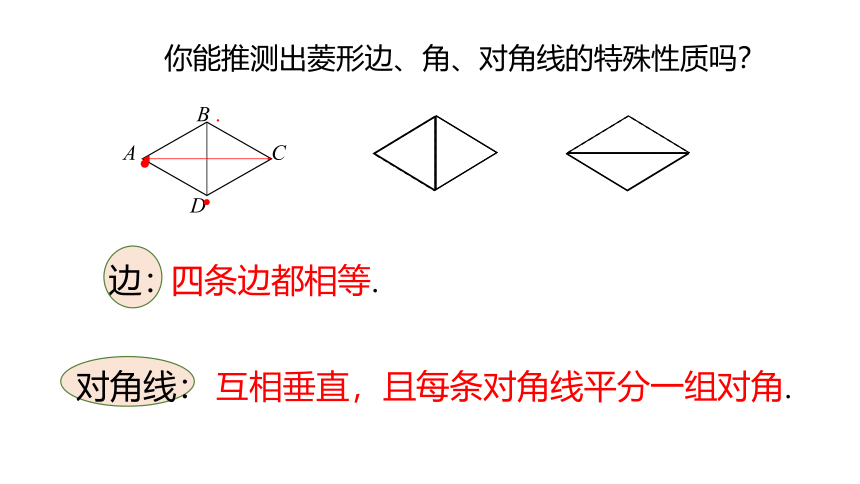
你能推测出菱形边、角、对角线的特殊性质吗?
边:
对角线:
四条边都相等.
互相垂直,且每条对角线平分一组对角.
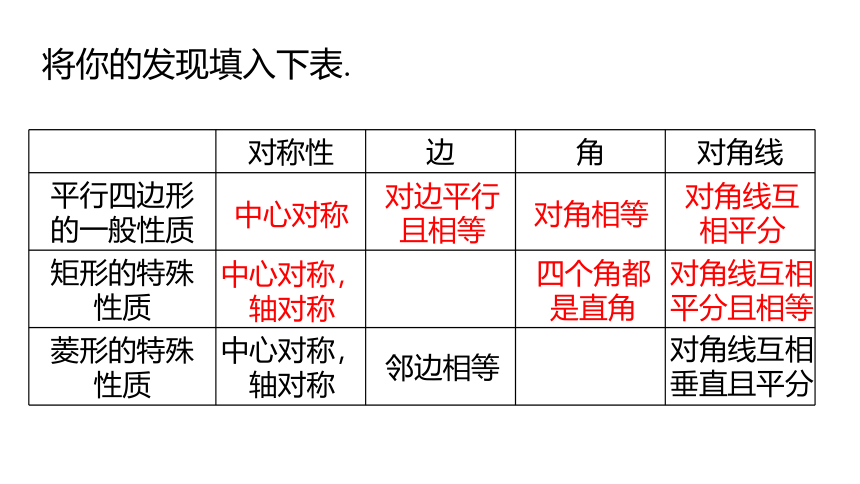
对称性 边 角 对角线
平行四边形的一般性质
矩形的特殊性质
菱形的特殊性质
将你的发现填入下表.
中心对称
对边平行且相等
对角相等
对角线互相平分
中心对称,
轴对称
四个角都是直角
对角线互相平分且相等
中心对称,
轴对称
邻边相等
对角线互相垂直且平分
菱形的性质1:菱形的四条边都相等.
A
B
C
D
归纳总结
几何语言:
∵四边形ABCD是菱形
∴AB=BC=CD=DA.
已知:如图,四边ABCD是菱形
求证:AB=BC=CD=AD
证明:∵四边形ABCD是菱形
∴ AB=CD,AD=BC (平行四边形的两组对边分别相等)
∵ AB=BC(菱形的定义)
∴ AB=BC=CD=AD
验证
A
B
C
D
菱形的性质2:菱形的两条对角线互相垂直.
A
B
C
D
O
归纳总结
几何语言:
∵四边形ABCD是菱形,
∴AC⊥BD.
已知:如图,四边形ABCD是菱形.
求证:AC⊥BD.
A
B
C
D
O
验证
证明:∵四边形ABCD是菱形,
∴AD=AB(菱形的定义),
OD=OB (平行四边形的对角线互相平分),
∴ AC ⊥ DB (三线合一).
A
B
C
D
O
菱形的两条对角线把菱形分割成四个全等的直角三角形
例题讲解
例1 如图,在菱形ABCD中,∠BAD=2∠B,试求出∠B的大小,并说明△ABC是等边三角形.
解:在菱形ABCD中, AB=BC
∠B+∠BAD=180°
又已知∠BAD=2∠B
可得∠B=60°
所以△ABC是一个角为60°的等腰三角形,即为等边三角形.
A
B
C
D
随堂演练
1.菱形具有而一般平行四边形不具有的性质是( )
A.对角相等 B.对边相等
C.对角线互相垂直 D.对角线相等
C
2.如图,在菱形ABCD中,AB=5,∠BCD=120°,则△ABC的周长等于( )
A.20
B.15
C.10
D.5
B
3.如图,在菱形ABCD中,AC=8,BD=6,则△ABD的周长等于( )
A.18 B.16 C.15 D.14
B
D
A
B
C
O
4. 如图,在△ABC中,AB=AC,四边形ADEF是菱形.
求证:BE=CE.
证明:∵四边形ADEF是菱形,
∴DE=FE,AB//FE,DE//AC,
∴∠B=∠CEF,∠C=∠BED.
∵AB=AC,
∴∠B=∠C,
∴∠BED=∠CEF.
在△DBE和△FCE中,
∵∠B=∠C,∠BED=∠CEF,DE=FE,
∴△DBE≌△FCE,
∴BE=CE.
课堂小结
菱形的性质
边
角
对角线
1.两组对边平行且相等;
2.四条边相等.
1.两组对角分别相等,
2.邻角互补.
两条对角线互相垂直平分
第19章 矩形、菱形和正方形
19.2.1 第1课时 菱形的性质
情景导入
将一张矩形的纸对折,再对折,
然后沿着图中的虚线剪下,打开,
你发现这是一个什么样的图形?
对边相等吗?是什么图形?
邻边相等吗?是什么图形?
平行四边形
答案马上揭晓!
相等
相等
获取新知
定义:有一组邻边相等的平行四边形叫做菱形.
上面得到图形是一个什么样的图形?
菱形
你能举出一些形状是菱形的例子吗?
铁丝网
衣帽架
带图案的衣服
中国结
(1)菱形必须满足两个条件:一是平行四边形; 二是一组邻边相等.二者必须同时具备,缺一不可;
(2)菱形的定义既是菱形的基本性质,也是菱形的基本判定方法.
菱形是轴对称图形吗
菱形是中心对称图形吗?
.C
D
B .
A .
.
是中心对称图形,对称中心为对角线交点
.
是轴对称图形,对称轴为它的对角线所在的直线.
.C
D
B .
A .
.
.
你能推测出菱形边、角、对角线的特殊性质吗?
边:
对角线:
四条边都相等.
互相垂直,且每条对角线平分一组对角.
对称性 边 角 对角线
平行四边形的一般性质
矩形的特殊性质
菱形的特殊性质
将你的发现填入下表.
中心对称
对边平行且相等
对角相等
对角线互相平分
中心对称,
轴对称
四个角都是直角
对角线互相平分且相等
中心对称,
轴对称
邻边相等
对角线互相垂直且平分
菱形的性质1:菱形的四条边都相等.
A
B
C
D
归纳总结
几何语言:
∵四边形ABCD是菱形
∴AB=BC=CD=DA.
已知:如图,四边ABCD是菱形
求证:AB=BC=CD=AD
证明:∵四边形ABCD是菱形
∴ AB=CD,AD=BC (平行四边形的两组对边分别相等)
∵ AB=BC(菱形的定义)
∴ AB=BC=CD=AD
验证
A
B
C
D
菱形的性质2:菱形的两条对角线互相垂直.
A
B
C
D
O
归纳总结
几何语言:
∵四边形ABCD是菱形,
∴AC⊥BD.
已知:如图,四边形ABCD是菱形.
求证:AC⊥BD.
A
B
C
D
O
验证
证明:∵四边形ABCD是菱形,
∴AD=AB(菱形的定义),
OD=OB (平行四边形的对角线互相平分),
∴ AC ⊥ DB (三线合一).
A
B
C
D
O
菱形的两条对角线把菱形分割成四个全等的直角三角形
例题讲解
例1 如图,在菱形ABCD中,∠BAD=2∠B,试求出∠B的大小,并说明△ABC是等边三角形.
解:在菱形ABCD中, AB=BC
∠B+∠BAD=180°
又已知∠BAD=2∠B
可得∠B=60°
所以△ABC是一个角为60°的等腰三角形,即为等边三角形.
A
B
C
D
随堂演练
1.菱形具有而一般平行四边形不具有的性质是( )
A.对角相等 B.对边相等
C.对角线互相垂直 D.对角线相等
C
2.如图,在菱形ABCD中,AB=5,∠BCD=120°,则△ABC的周长等于( )
A.20
B.15
C.10
D.5
B
3.如图,在菱形ABCD中,AC=8,BD=6,则△ABD的周长等于( )
A.18 B.16 C.15 D.14
B
D
A
B
C
O
4. 如图,在△ABC中,AB=AC,四边形ADEF是菱形.
求证:BE=CE.
证明:∵四边形ADEF是菱形,
∴DE=FE,AB//FE,DE//AC,
∴∠B=∠CEF,∠C=∠BED.
∵AB=AC,
∴∠B=∠C,
∴∠BED=∠CEF.
在△DBE和△FCE中,
∵∠B=∠C,∠BED=∠CEF,DE=FE,
∴△DBE≌△FCE,
∴BE=CE.
课堂小结
菱形的性质
边
角
对角线
1.两组对边平行且相等;
2.四条边相等.
1.两组对角分别相等,
2.邻角互补.
两条对角线互相垂直平分
