华师大版数学八年级下册19.2.1 第2课时 菱形性质的应用 同步课件(共15张PPT)
文档属性
| 名称 | 华师大版数学八年级下册19.2.1 第2课时 菱形性质的应用 同步课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 185.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
第19章 矩形、菱形和正方形
19.2.1 第2课时 菱形性质的应用
知识回顾
菱形的性质有哪些?
边
对角线
菱形的四条边都相等
菱形的两条对角线互相垂直且平分
下面的问题都和菱形的性质有关,你能运用它解决这些问题吗?
菱形具有平行四边形的一切性质;
获取新知
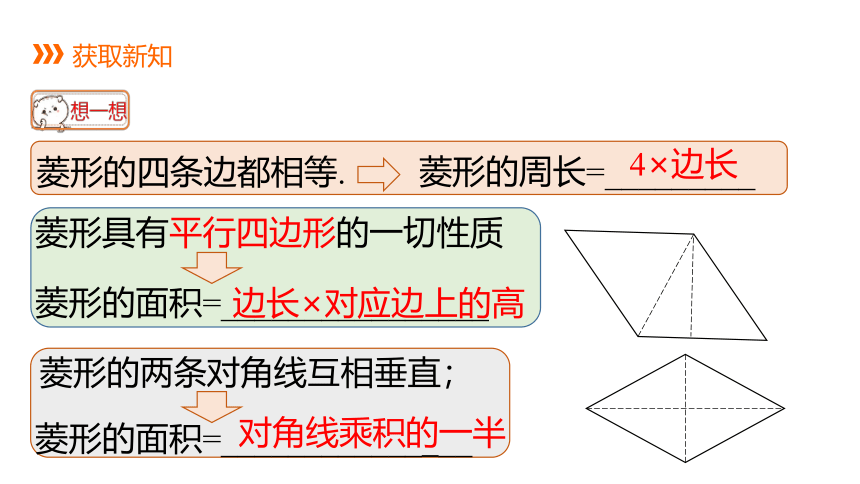
菱形的四条边都相等.
菱形的周长=_________
菱形具有平行四边形的一切性质
菱形的面积=________________
菱形的两条对角线互相垂直;
菱形的面积=____________ __
4×边长
边长×对应边上的高
对角线乘积的一半
解:①∵菱形ABCD,
∴AB=AD (菱形的四条边都相等)
又∵AB=BD (已知)
∴在△ABD中,AB=AD=BD
即△ABD是等边三角形
∴∠ABD=60°
例1 如图,菱形ABCD中,AB=BD=2cm,
求①∠ABC的度数,②菱形ABCD的周长。
D
A
B
C
例题讲解
∴∠ABC= 2∠ABD=120°(菱形对角线平分对角)
②∵在菱形ABCD中,AB=BC=CD=DA
AB=BD=2cm(已知)
∴菱形ABCD的周长=2 ×4= 8(cm)
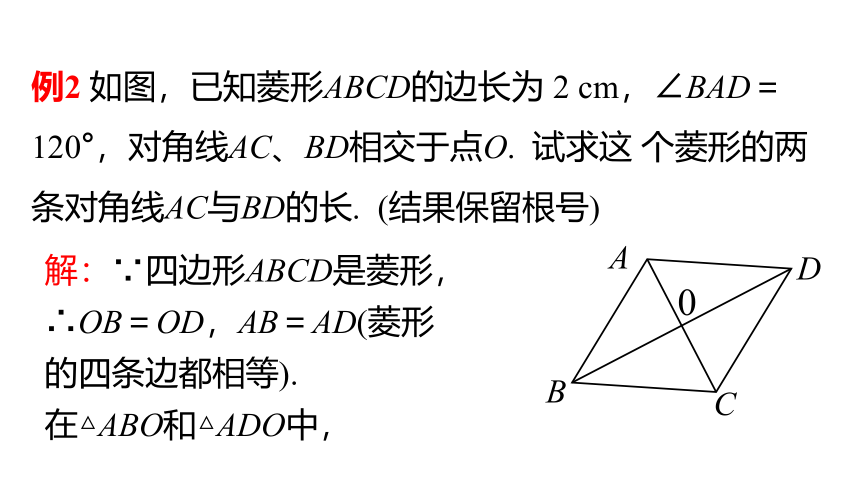
例2 如图,已知菱形ABCD的边长为 2 cm,∠BAD=120°,对角线AC、BD相交于点O. 试求这 个菱形的两条对角线AC与BD的长. (结果保留根号)
D
A
B
C
0
解:∵四边形ABCD是菱形,
∴OB=OD,AB=AD(菱形的四条边都相等).
在△ABO和△ADO中,
解:
∵AB=AD,AO=AO, OB=OD,
∴△ABO≌△ADO,
∴∠BAO=∠DAO = ∠BAD=60°.
在△ABC中,∵AB=BC,∠BAC=60°,
∴△ABC为等边三角形,∴AC=AB=2.
在菱形ABCD中,∵AC⊥BD(菱形的对角线互相垂直),
∴△AOB为直角三角形,
∴
∴
例3 如图,菱形ABCD的对角线AC与BD 相交于点O,AE垂直且平分CD,垂足为点E. 求∠BCD的大小.
D
A
B
C
0
E
∵四边形ABCD是菱形,
∴AD=DC=CB=BA(菱形的
四条边都相等).
解:
又∵AE垂直平分CD,
∴AC=AD,
∴AC=AD=DC=CB=BA,
即△ADC与△ABC都为等边三角形,
∴∠ACD=∠ACB=60°.
∴∠BCD=120°.
D
A
B
C
0
1. 一个菱形的周长为8cm,一条对角线长为2cm.则这个菱形的四个内角的度数为 ____ ___ _____
_____.
60°
120°
60°
120°
随堂演练
2. 如图,菱形ABCD的边长为2cm,E是AB的中点,且DE⊥AB,则菱形ABCD的面积为 cm
D
A
B
C
E
3.在菱形ABCD中,AC与BD交于点O, AC=8, BD=6.则: AB= , 菱形ABCD的周长为 ; 若OE⊥BC于E,则OE= ;若点F为BC中点,则OF=______ .
5
20
2.4
2.5
4. 已知如图,菱形ABCD中,E是AB的中点,且DE ⊥ AB, AB=2。求(1)∠ABC的度数;(2)对角线AC、BD的长;(3)菱形ABCD的面积。
解:(1)∵E为AB的中点,DE⊥AB,
∴AD=BD,
∵菱形ABCD中,AD=AB,
∴AD=AB=BD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∴∠ABC=120°;
(2)∵△ABD是等边三角形,AE=2,
∴AB=BD=AD=4,
∴DE=AO=
∴AC= ;
(3)菱形ABCD的面积= BD AC= × ×4=8
课堂小结
菱形性质的应用
计算公式
问题分类
1.周长=边长的四倍
2.面积=底×高=两条对角线乘积的一半
线段问题
角的问题
面积问题
第19章 矩形、菱形和正方形
19.2.1 第2课时 菱形性质的应用
知识回顾
菱形的性质有哪些?
边
对角线
菱形的四条边都相等
菱形的两条对角线互相垂直且平分
下面的问题都和菱形的性质有关,你能运用它解决这些问题吗?
菱形具有平行四边形的一切性质;
获取新知
菱形的四条边都相等.
菱形的周长=_________
菱形具有平行四边形的一切性质
菱形的面积=________________
菱形的两条对角线互相垂直;
菱形的面积=____________ __
4×边长
边长×对应边上的高
对角线乘积的一半
解:①∵菱形ABCD,
∴AB=AD (菱形的四条边都相等)
又∵AB=BD (已知)
∴在△ABD中,AB=AD=BD
即△ABD是等边三角形
∴∠ABD=60°
例1 如图,菱形ABCD中,AB=BD=2cm,
求①∠ABC的度数,②菱形ABCD的周长。
D
A
B
C
例题讲解
∴∠ABC= 2∠ABD=120°(菱形对角线平分对角)
②∵在菱形ABCD中,AB=BC=CD=DA
AB=BD=2cm(已知)
∴菱形ABCD的周长=2 ×4= 8(cm)
例2 如图,已知菱形ABCD的边长为 2 cm,∠BAD=120°,对角线AC、BD相交于点O. 试求这 个菱形的两条对角线AC与BD的长. (结果保留根号)
D
A
B
C
0
解:∵四边形ABCD是菱形,
∴OB=OD,AB=AD(菱形的四条边都相等).
在△ABO和△ADO中,
解:
∵AB=AD,AO=AO, OB=OD,
∴△ABO≌△ADO,
∴∠BAO=∠DAO = ∠BAD=60°.
在△ABC中,∵AB=BC,∠BAC=60°,
∴△ABC为等边三角形,∴AC=AB=2.
在菱形ABCD中,∵AC⊥BD(菱形的对角线互相垂直),
∴△AOB为直角三角形,
∴
∴
例3 如图,菱形ABCD的对角线AC与BD 相交于点O,AE垂直且平分CD,垂足为点E. 求∠BCD的大小.
D
A
B
C
0
E
∵四边形ABCD是菱形,
∴AD=DC=CB=BA(菱形的
四条边都相等).
解:
又∵AE垂直平分CD,
∴AC=AD,
∴AC=AD=DC=CB=BA,
即△ADC与△ABC都为等边三角形,
∴∠ACD=∠ACB=60°.
∴∠BCD=120°.
D
A
B
C
0
1. 一个菱形的周长为8cm,一条对角线长为2cm.则这个菱形的四个内角的度数为 ____ ___ _____
_____.
60°
120°
60°
120°
随堂演练
2. 如图,菱形ABCD的边长为2cm,E是AB的中点,且DE⊥AB,则菱形ABCD的面积为 cm
D
A
B
C
E
3.在菱形ABCD中,AC与BD交于点O, AC=8, BD=6.则: AB= , 菱形ABCD的周长为 ; 若OE⊥BC于E,则OE= ;若点F为BC中点,则OF=______ .
5
20
2.4
2.5
4. 已知如图,菱形ABCD中,E是AB的中点,且DE ⊥ AB, AB=2。求(1)∠ABC的度数;(2)对角线AC、BD的长;(3)菱形ABCD的面积。
解:(1)∵E为AB的中点,DE⊥AB,
∴AD=BD,
∵菱形ABCD中,AD=AB,
∴AD=AB=BD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∴∠ABC=120°;
(2)∵△ABD是等边三角形,AE=2,
∴AB=BD=AD=4,
∴DE=AO=
∴AC= ;
(3)菱形ABCD的面积= BD AC= × ×4=8
课堂小结
菱形性质的应用
计算公式
问题分类
1.周长=边长的四倍
2.面积=底×高=两条对角线乘积的一半
线段问题
角的问题
面积问题
