华师大版数学八年级下册同步课件:17.3.1 一次函数(共20张PPT)
文档属性
| 名称 | 华师大版数学八年级下册同步课件:17.3.1 一次函数(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 12:42:56 | ||
图片预览








文档简介
(共20张PPT)
第17章 函数及其图象
17.3.1 一次函数
情境导入
小明暑假第一次去北京.汽车驶上A地的高速公路后,小明观察里程碑,发现汽车的平均车速是95千米/小时.已知A地直达北京的高速公路全程为570千米。
问题
小明能根据行驶时间估计自己和北京的距离吗?
分析:我们知道汽车距北京的路程随着行车时间的变化而变化,要想找出这两个变量的关系,并据此得出相应的值,显然,应该探求这两个变量的变化规律.为此,我们设汽车在高速公路上行驶时间为t时,汽车距北京的路程为s千米,根据题意,s和t的函数关系式是s=570-95t.这样小明根据行驶的时间就能计算出到北京的距离。
你能举出一个类似这样函数关系的例子吗?
弹簧下端悬挂重物,弹簧的长度会伸长,弹簧的长度y(厘米)是所挂重物质量x(千克)的函数,已知一根弹簧在不挂重物时长6厘米,在一定的弹性限度内,每挂1千克重物弹簧伸长0.3厘米,根据所给条件完成下列问题:
探究
获取新知
(1)计算所挂物体的质量分别为0 kg、1 kg、2 kg、3 kg、4 kg、5 kg时的弹簧长度,并填入下表:
x/kg 0 1 2 3 4 5
y/cm
(2)你能写出x与y之间的函数关系式吗?
6
6.3
6.6
6.9
7.2
7.5
解:因为每挂1千克重物弹簧伸长0.3厘米,所以挂x千克重物时,弹簧伸长0.3x厘米,又因为不挂重物时弹簧的长度为6厘米,所以挂x厘米重物时弹簧的长度为(0.3x+6)厘米,即有
上面的两个函数关系式:
(1)s=570-95t
(2) y=0.3x+6
大家讨论一下,这两个函数关系式有什么特点
①等号的右边都有 项;
②这两项分别为关于自变量的 项, 项。
2
常数
一次
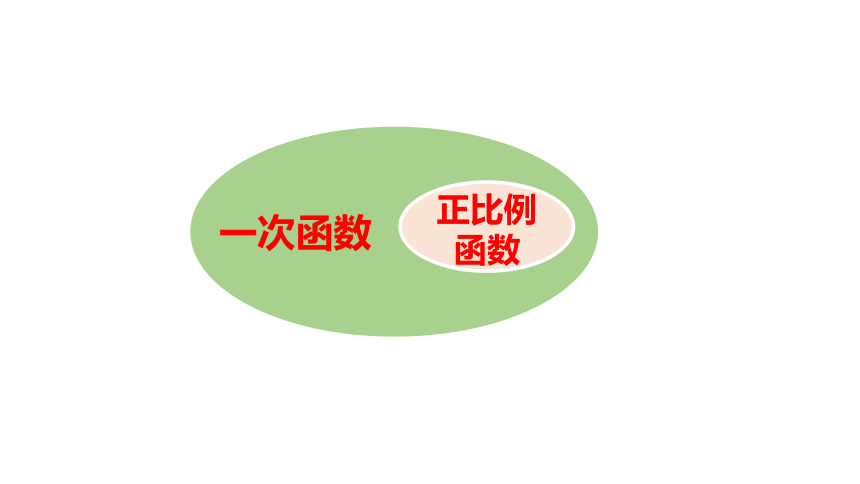
若两个变量 x、y之间的关系可以表示成y=kx+b(k,b为常数,k≠0)的形式,则称 y是x的一次函数.(x为自变量,y为因变量.)
特别地,当b=0时,y=kx,称y是x的正比例函数.
y=kx+ b (k,b为常数,k≠0)
一次项
常数项
一次项系数
一次函数
正比例
函数
下列函数中,哪些是一次函数?哪些是正比例函数?系数 k 和常数项b的值各是多少?
一次函数
一次函数
正比例函数
?
不是一次函数,也不是正比例函数
1.判断一个函数是一次函数的条件:
自变量是一次整式,一次项系数不为零;
2.判断一个函数是正比例函数的条件:
自变量是一次整式,一次项系数不为零,常数项为零.
例题讲解
例1 已知函数y=(m-3)x|m|-2+n-2,求符合下列条件的
m,n的值:
(1)此函数是一次函数;
(2)此函数是正比例函数.
解: (1)由|m|-2=1得m=±3.
∵m-3≠0,∴m≠3,
∴当m=-3,n为任意实数时此函数是一次函数.
(2)由|m|-2=1得m=±3.
∵m-3≠0,n-2=0,
∴m≠3,n=2,
∴当m=-3,n=2时此函数是正比例函数.
例2 写出下列各题中x与y之间的函数关系式,并判断:y是否为x的一次函数?是否为正比例函数?
(1)汽车以60千米/时的速度匀速行驶,行驶路程y(千米)与行驶时间x(时)之间的关系;
(2)圆的面积S(厘米2)与它的半径r(厘米)之间的关系;
(3)某水池有水15立方米,现打开进水管进水,进水速度为5立方米/时,x小时后这个水池内有水y立方米.
解:(1)由“路程=速度×时间”,得y=60x,y是x的
一次函数,也是x的正比例函数.
(2)由圆的面积公式,得S=πr2,S不是r的一次函数,
也不是r的正比例函数.
(3)这个水池每时增加5立方米的水,x小时后增加5x
立方米的水,因而y=15+5x,y是x的一次函数,
但不是x的正比例函数.
随堂演练
1.下列函数中,y是x的一次函数的是( )
A.y=x2+2x B.y=-
C.y=x D.y= +11.
C
2.下列y关于x的函数中,是正比例函数的是( )
A.y=x2 B.y=
C.y= D.y=
C
(1) 当m = 时,y是x的正比例函数;
3、已知函数y=(m-3)xm-1;
(2) 若x=-2, y=a 满足(1)中所求的函数关系式,则a= .
2
2
4.仓库内原有粉笔400盒.如果每个星期领出36盒,求仓库内余下的粉笔盒数Q与星期数t之间的函数关系式.
解: Q=400-36t(0≤t≤11且t为整数).
课堂小结
一次函数
一次函数的概念
根据实际问题列函数关系式
正比例函数
y=kx+b(k,b是常数,且k≠0).
y=kx(常数k≠0)
第17章 函数及其图象
17.3.1 一次函数
情境导入
小明暑假第一次去北京.汽车驶上A地的高速公路后,小明观察里程碑,发现汽车的平均车速是95千米/小时.已知A地直达北京的高速公路全程为570千米。
问题
小明能根据行驶时间估计自己和北京的距离吗?
分析:我们知道汽车距北京的路程随着行车时间的变化而变化,要想找出这两个变量的关系,并据此得出相应的值,显然,应该探求这两个变量的变化规律.为此,我们设汽车在高速公路上行驶时间为t时,汽车距北京的路程为s千米,根据题意,s和t的函数关系式是s=570-95t.这样小明根据行驶的时间就能计算出到北京的距离。
你能举出一个类似这样函数关系的例子吗?
弹簧下端悬挂重物,弹簧的长度会伸长,弹簧的长度y(厘米)是所挂重物质量x(千克)的函数,已知一根弹簧在不挂重物时长6厘米,在一定的弹性限度内,每挂1千克重物弹簧伸长0.3厘米,根据所给条件完成下列问题:
探究
获取新知
(1)计算所挂物体的质量分别为0 kg、1 kg、2 kg、3 kg、4 kg、5 kg时的弹簧长度,并填入下表:
x/kg 0 1 2 3 4 5
y/cm
(2)你能写出x与y之间的函数关系式吗?
6
6.3
6.6
6.9
7.2
7.5
解:因为每挂1千克重物弹簧伸长0.3厘米,所以挂x千克重物时,弹簧伸长0.3x厘米,又因为不挂重物时弹簧的长度为6厘米,所以挂x厘米重物时弹簧的长度为(0.3x+6)厘米,即有
上面的两个函数关系式:
(1)s=570-95t
(2) y=0.3x+6
大家讨论一下,这两个函数关系式有什么特点
①等号的右边都有 项;
②这两项分别为关于自变量的 项, 项。
2
常数
一次
若两个变量 x、y之间的关系可以表示成y=kx+b(k,b为常数,k≠0)的形式,则称 y是x的一次函数.(x为自变量,y为因变量.)
特别地,当b=0时,y=kx,称y是x的正比例函数.
y=kx+ b (k,b为常数,k≠0)
一次项
常数项
一次项系数
一次函数
正比例
函数
下列函数中,哪些是一次函数?哪些是正比例函数?系数 k 和常数项b的值各是多少?
一次函数
一次函数
正比例函数
?
不是一次函数,也不是正比例函数
1.判断一个函数是一次函数的条件:
自变量是一次整式,一次项系数不为零;
2.判断一个函数是正比例函数的条件:
自变量是一次整式,一次项系数不为零,常数项为零.
例题讲解
例1 已知函数y=(m-3)x|m|-2+n-2,求符合下列条件的
m,n的值:
(1)此函数是一次函数;
(2)此函数是正比例函数.
解: (1)由|m|-2=1得m=±3.
∵m-3≠0,∴m≠3,
∴当m=-3,n为任意实数时此函数是一次函数.
(2)由|m|-2=1得m=±3.
∵m-3≠0,n-2=0,
∴m≠3,n=2,
∴当m=-3,n=2时此函数是正比例函数.
例2 写出下列各题中x与y之间的函数关系式,并判断:y是否为x的一次函数?是否为正比例函数?
(1)汽车以60千米/时的速度匀速行驶,行驶路程y(千米)与行驶时间x(时)之间的关系;
(2)圆的面积S(厘米2)与它的半径r(厘米)之间的关系;
(3)某水池有水15立方米,现打开进水管进水,进水速度为5立方米/时,x小时后这个水池内有水y立方米.
解:(1)由“路程=速度×时间”,得y=60x,y是x的
一次函数,也是x的正比例函数.
(2)由圆的面积公式,得S=πr2,S不是r的一次函数,
也不是r的正比例函数.
(3)这个水池每时增加5立方米的水,x小时后增加5x
立方米的水,因而y=15+5x,y是x的一次函数,
但不是x的正比例函数.
随堂演练
1.下列函数中,y是x的一次函数的是( )
A.y=x2+2x B.y=-
C.y=x D.y= +11.
C
2.下列y关于x的函数中,是正比例函数的是( )
A.y=x2 B.y=
C.y= D.y=
C
(1) 当m = 时,y是x的正比例函数;
3、已知函数y=(m-3)xm-1;
(2) 若x=-2, y=a 满足(1)中所求的函数关系式,则a= .
2
2
4.仓库内原有粉笔400盒.如果每个星期领出36盒,求仓库内余下的粉笔盒数Q与星期数t之间的函数关系式.
解: Q=400-36t(0≤t≤11且t为整数).
课堂小结
一次函数
一次函数的概念
根据实际问题列函数关系式
正比例函数
y=kx+b(k,b是常数,且k≠0).
y=kx(常数k≠0)
