河北省沧衡八校联盟2021-2022学年高二下学期期中考试数学试题(Word版含解析)
文档属性
| 名称 | 河北省沧衡八校联盟2021-2022学年高二下学期期中考试数学试题(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 628.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 16:32:22 | ||
图片预览



文档简介
沧衡八校联盟2021-2022学年高二下学期期中考试
数学试题
注意事项:
1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡,上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
4.本试卷主要考试内容:人教A版选择性必修第二册第五章,选择性必修第三册.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.从8瓶酸牛奶和4瓶纯牛奶中任意选取4瓶,则恰有1瓶是酸牛奶的选取方法共有( )
A.24种 B.32种 C.48种 D.64种
2.已知函数,则在上的平均变化率为( )
A. B. C.2 D.3
3.已知,则( )
A.2 B. C. D.
4.3名男生,2名女生站成一排照相,则2名女生相邻且都不站在最左端的不同的站法共有( )
A.72种 B.64种 C.48种 D.36种
5.已知是函数的导函数,函数的图象如图所示,则的极大值点为( )
A. B. C. D.
6.甲、乙、丙三人报考,,三所大学,每人限报一所,设事件为“三人报考的大学均不相同”,事件为“甲报考的大学与其他两人均不相同”,则概率( )
A. B. C. D.
7.下列结论正确的是( )
A.若,,是一组两两相互独立的事件,则
B.若,事件满足,则,是对立事件
C.若,是互斥事件,则
D.“,是互斥事件”是“,是对立事件”的充分不必要条件
8.已知,则( )
A.2022 B.
C.4044 D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知随机变量的分布列为
1 2 3
0.3
则( )
A. B.
C. D.
10.随着美丽乡村创建和乡村振兴战略的实施,乡村发生了翻天覆地的变化.在农产品展销会.上,某村的农产品红茶和绿茶的日销量分别服从正态分布和,它们的正态分布密度曲线如图所示,则下列结论不正确的有(参考数据:若随机变量服从正态分布,则,,)( )
A.红茶日销售量的稳定性低于绿茶日销量的稳定性
B.红茶日销售量的平均值大于绿茶日销量的平均值
C.红茶日销量在内的概率约为0.49865
D.绿茶日销量在内的概率约为0.34135
11.在某城市中,,两地之间有如图所示的道路网,甲随机沿路网选择一条最短路径,从地出发去往地.下列结论正确的有( )
A.不同的路径共有31条
B.不同的路径共有61条
C.若甲途经地,则不同的路径共有18条
D.若甲途经地,且不经过地,则不同的路径共有9条
12.已知,,,则( )
A. B. C. D.
三、填空题:本题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.的展开式中,常数项为______.
14.已知函数,则______.
15.25名防疫志愿者组成5行5列的方阵,现从中选出2人,则不同的选法种数为______;若选出的2人既不在同一行又不在同一列,则不同的选法种数为______.(本题第一空2分,第二空3分)
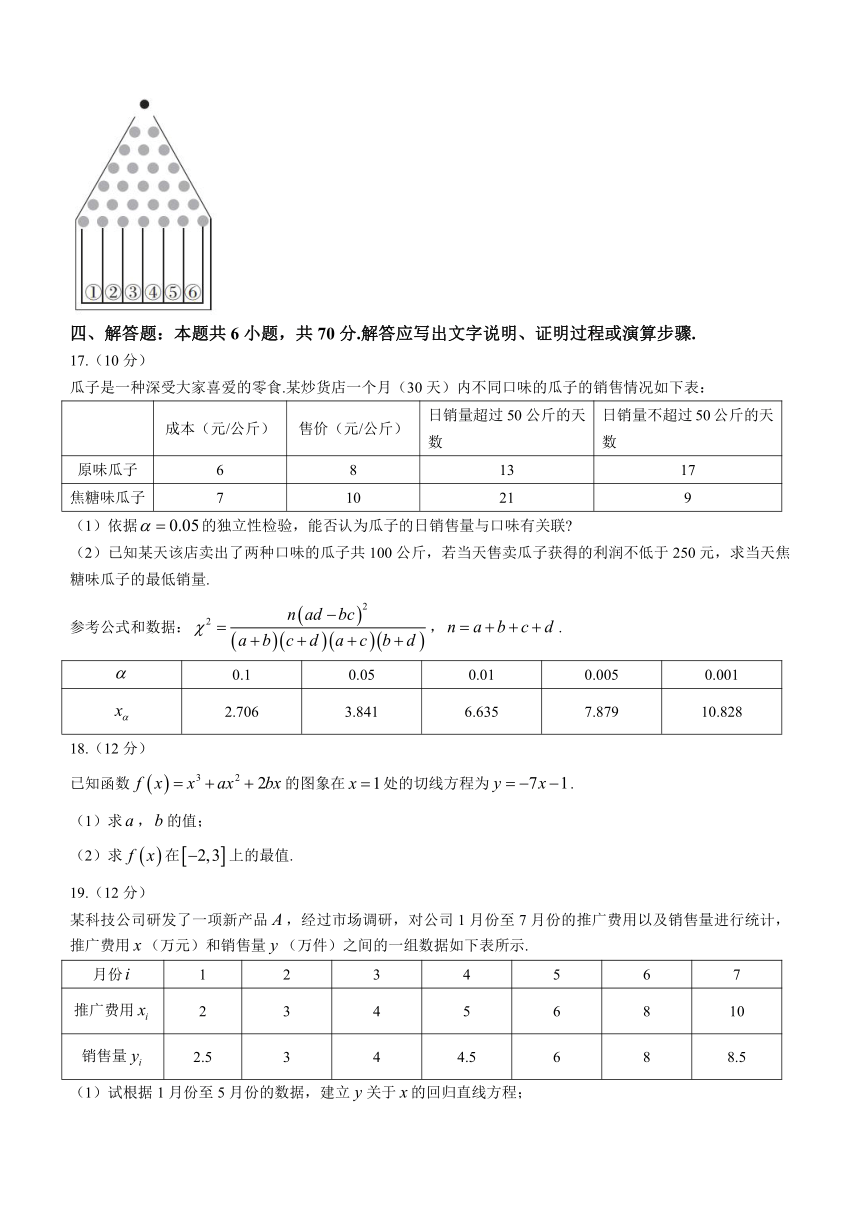
16.如图所示的是一种类似于高尔顿板的装置示意图.在一块木板上钉着6排互相平行但相互错开的圆柱形小木钉,小木钉之间留有适当的空隙作为通道,前面挡有一块玻璃.将小球从顶端放入,小球下落的过程中,每次碰到小木钉后向左或向右落下,最后掉入下方的某一个球槽内.若小球下落过程中向左落下的概率为,则小球最终落入④号球槽的概率为______.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
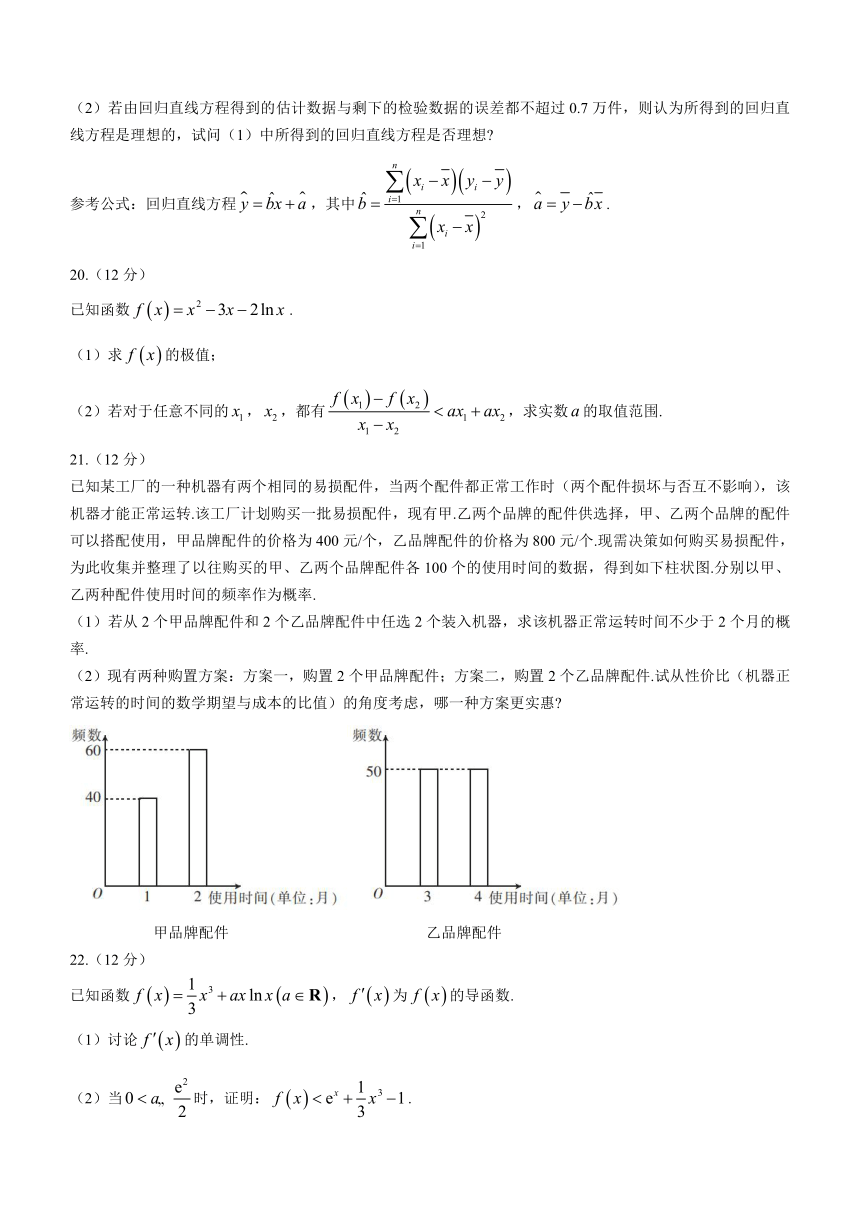
17.(10分)
瓜子是一种深受大家喜爱的零食.某炒货店一个月(30天)内不同口味的瓜子的销售情况如下表:
成本(元/公斤) 售价(元/公斤) 日销量超过50公斤的天数 日销量不超过50公斤的天数
原味瓜子 6 8 13 17
焦糖味瓜子 7 10 21 9
(1)依据的独立性检验,能否认为瓜子的日销售量与口味有关联
(2)已知某天该店卖出了两种口味的瓜子共100公斤,若当天售卖瓜子获得的利润不低于250元,求当天焦糖味瓜子的最低销量.
参考公式和数据:,.
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
18.(12分)
已知函数的图象在处的切线方程为.
(1)求,的值;
(2)求在上的最值.
19.(12分)
某科技公司研发了一项新产品,经过市场调研,对公司1月份至7月份的推广费用以及销售量进行统计,推广费用(万元)和销售量(万件)之间的一组数据如下表所示.
月份 1 2 3 4 5 6 7
推广费用 2 3 4 5 6 8 10
销售量 2.5 3 4 4.5 6 8 8.5
(1)试根据1月份至5月份的数据,建立关于的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差都不超过0.7万件,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想
参考公式:回归直线方程,其中,.
20.(12分)
已知函数.
(1)求的极值;
(2)若对于任意不同的,,都有,求实数的取值范围.
21.(12分)
已知某工厂的一种机器有两个相同的易损配件,当两个配件都正常工作时(两个配件损坏与否互不影响),该机器才能正常运转.该工厂计划购买一批易损配件,现有甲.乙两个品牌的配件供选择,甲、乙两个品牌的配件可以搭配使用,甲品牌配件的价格为400元/个,乙品牌配件的价格为800元/个.现需决策如何购买易损配件,为此收集并整理了以往购买的甲、乙两个品牌配件各100个的使用时间的数据,得到如下柱状图.分别以甲、乙两种配件使用时间的频率作为概率.
(1)若从2个甲品牌配件和2个乙品牌配件中任选2个装入机器,求该机器正常运转时间不少于2个月的概率.
(2)现有两种购置方案:方案一,购置2个甲品牌配件;方案二,购置2个乙品牌配件.试从性价比(机器正常运转的时间的数学期望与成本的比值)的角度考虑,哪一种方案更实惠
甲品牌配件 乙品牌配件
22.(12分)
已知函数,为的导函数.
(1)讨论的单调性.
(2)当时,证明:.
沧衡八校联盟2021-2022学年高二下学期期中考试
数学试题参考答案
1.B 恰有1瓶是酸牛奶的选取方法有种.
2.A 在上的平均变化率为
3.C 因为,所以
4.D 不同的站法共有种.
5.A 由图可知,当时,;当时,.所以的单调递增区间为和,单调递减区间为.故的极大值点为.
6.D 每人报考大学有3种选择,故总的报考方法共有种,三人所报考的大学均不相同的报考方法有种,甲报考的大学与其他两人均不相同的报考方法有种,故
7.C 对于选项A,例如,从1,2,3,4中随机选出一个数字,记事件为“选出的数字为1或2”,事件为“选出的数字为1或3”,事件为“选出的数字为1或4”,则事件,,,同时发生的事件为“选出的数字为1”,因为,,所以,,,故,,是一组两两独立的事件,但是,A不正确.对于选项B,例如,投掷一枚质地均匀的骰子,记事件为“点数为1,2,3”,事件为“点数为2,4,6”,则,但是,不是对立事件,B不正确.对于选项C,因为,是互斥事件,所以为必然事件,则,C正确.对于选项D,互斥事件不一定是对立事件,对立事件一定是互斥事件,所以“,是互斥事件”是“,是对立事件”的必要不充分条件,D不正确.
8.B 两边求导,得.
令,得,
令,得,
所以.
9.AC 由,得,则.
10.BD 由正态分布密度曲线可知,红茶和绿茶日销量的平均值相等,B不正确.越小,图象越瘦、高,数据越稳定,所以绿茶日销量的稳定性高于红茶日销量的稳定性,A正确.红茶日销量在内的概率约为,C正确.绿茶日销量在内的概率约为,D不正确.
11.ACD 由图可知,从地出发去往地的最短路径共包含7步,其中3步向上,4步向右,且前3步中,至少有1步向上,则不同的路径共有条.若甲途经地,则不同的路径共有条.若甲途经地,且不经过地,则不同的路径共有条.故选ACD.
12.ABC 令函数,则.当时,,在上单调递增,则,即,故,B正确.令函数,则,当时,,在上单调递增,则,故,A,C正确,D不正确.
13. ,令,得,所以.
14. 因为
所以,所以解得,
故
15.300;200 从25人中选出2人,共有种选法,若选出的2人既不在同一行又不在同一列,则共有种选法.
16. 小球最终落人④号球槽,共有5步,其中3步向右,2步向左,故所求概率为
17.解:(1)零假设:瓜子的日销售量与口味无关联.
由题可知,
根据小概率值的独立性检验,我们推断不成立,故认为瓜子的日销售量与口味有关联,此推断犯错误的概率不大于0.05.
(2)由题可知,每公斤原味瓜子的利润为2元,每公斤焦糖味瓜子的利润为3元
设当天焦糖味瓜子的销量为公斤,则,
解得,故当天焦糖味瓜子的最低销量为50公斤.
18.解:(1)因为,所以,
又的图象在处的切线方程为,所以
解得
(2)由(1)可知,,
则当时,;当时,
又,
所以在上的最大值为,最小值为
19.解:(1)因为,
所以,
所以,于是关于的回归直线方程为
(2)当时,,则,
当时,,则,
故可以认为(1)中所得到的回归直线方程是理想的.
20.解:(1)因为,所以
令,解得或(舍去).
当变化时,,的变化情况如表所示.
2
0
单调递减 单调递增
因此,当时,有极小值,且极小值为,无极大值
(2)不妨令,则等价于,即
令函数,可知在上单调递减,
若,即,则在上恒成立,故在上恒成立,
则在上单调递减,符合题意
若,即,则在上不恒成立,故在上不恒成立,则在上不可能单调递减,不符合题意.
综上所述,实数的取值范围为
21.解:(1)若装入2个甲品牌的配件,则该机器正常运转时间不少于2个月的概率为
若装入2个乙品牌的配件,则该机器正常运转时间不少于2个月的概率为
若装入1个甲品牌和1个乙品牌的配件,则该机器正常运转时间不少于2个月的概率为
故该机器正常运转时间不少于2个月的概率为
(2)若采用方案一,设机器可正常运转的时间为(单位:月),则的可能取值为1,2,
且,
所以的分布列为
1 2
,它与购置配件的成本之比为
若采用方案二,设机器可正常运转的时间为(单位:月),则的可能取值为3,4,
且,
所以的分布列为
3 4
,它与购置配件的成本之比为,
因为,所以从性价比的角度考虑,方案二更实惠.
22.(1)解:因为,所以
令函数,则.
若,则在上恒成立.
若,则当时,;
当时,
故当时,在上单调递增;
当时,在上单调递增,在上单调递减.
(2)证明:要证,即证.
当时,,,故.
当时,要证,即证
令函数,则
当时,;当时,.
所以,故要证,只需证
令函数,则
令函数,则,则,即,
所以,所以,即
综上所述,当时,
数学试题
注意事项:
1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡,上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
4.本试卷主要考试内容:人教A版选择性必修第二册第五章,选择性必修第三册.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.从8瓶酸牛奶和4瓶纯牛奶中任意选取4瓶,则恰有1瓶是酸牛奶的选取方法共有( )
A.24种 B.32种 C.48种 D.64种
2.已知函数,则在上的平均变化率为( )
A. B. C.2 D.3
3.已知,则( )
A.2 B. C. D.
4.3名男生,2名女生站成一排照相,则2名女生相邻且都不站在最左端的不同的站法共有( )
A.72种 B.64种 C.48种 D.36种
5.已知是函数的导函数,函数的图象如图所示,则的极大值点为( )
A. B. C. D.
6.甲、乙、丙三人报考,,三所大学,每人限报一所,设事件为“三人报考的大学均不相同”,事件为“甲报考的大学与其他两人均不相同”,则概率( )
A. B. C. D.
7.下列结论正确的是( )
A.若,,是一组两两相互独立的事件,则
B.若,事件满足,则,是对立事件
C.若,是互斥事件,则
D.“,是互斥事件”是“,是对立事件”的充分不必要条件
8.已知,则( )
A.2022 B.
C.4044 D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知随机变量的分布列为
1 2 3
0.3
则( )
A. B.
C. D.
10.随着美丽乡村创建和乡村振兴战略的实施,乡村发生了翻天覆地的变化.在农产品展销会.上,某村的农产品红茶和绿茶的日销量分别服从正态分布和,它们的正态分布密度曲线如图所示,则下列结论不正确的有(参考数据:若随机变量服从正态分布,则,,)( )
A.红茶日销售量的稳定性低于绿茶日销量的稳定性
B.红茶日销售量的平均值大于绿茶日销量的平均值
C.红茶日销量在内的概率约为0.49865
D.绿茶日销量在内的概率约为0.34135
11.在某城市中,,两地之间有如图所示的道路网,甲随机沿路网选择一条最短路径,从地出发去往地.下列结论正确的有( )
A.不同的路径共有31条
B.不同的路径共有61条
C.若甲途经地,则不同的路径共有18条
D.若甲途经地,且不经过地,则不同的路径共有9条
12.已知,,,则( )
A. B. C. D.
三、填空题:本题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.的展开式中,常数项为______.
14.已知函数,则______.
15.25名防疫志愿者组成5行5列的方阵,现从中选出2人,则不同的选法种数为______;若选出的2人既不在同一行又不在同一列,则不同的选法种数为______.(本题第一空2分,第二空3分)
16.如图所示的是一种类似于高尔顿板的装置示意图.在一块木板上钉着6排互相平行但相互错开的圆柱形小木钉,小木钉之间留有适当的空隙作为通道,前面挡有一块玻璃.将小球从顶端放入,小球下落的过程中,每次碰到小木钉后向左或向右落下,最后掉入下方的某一个球槽内.若小球下落过程中向左落下的概率为,则小球最终落入④号球槽的概率为______.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)
瓜子是一种深受大家喜爱的零食.某炒货店一个月(30天)内不同口味的瓜子的销售情况如下表:
成本(元/公斤) 售价(元/公斤) 日销量超过50公斤的天数 日销量不超过50公斤的天数
原味瓜子 6 8 13 17
焦糖味瓜子 7 10 21 9
(1)依据的独立性检验,能否认为瓜子的日销售量与口味有关联
(2)已知某天该店卖出了两种口味的瓜子共100公斤,若当天售卖瓜子获得的利润不低于250元,求当天焦糖味瓜子的最低销量.
参考公式和数据:,.
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
18.(12分)
已知函数的图象在处的切线方程为.
(1)求,的值;
(2)求在上的最值.
19.(12分)
某科技公司研发了一项新产品,经过市场调研,对公司1月份至7月份的推广费用以及销售量进行统计,推广费用(万元)和销售量(万件)之间的一组数据如下表所示.
月份 1 2 3 4 5 6 7
推广费用 2 3 4 5 6 8 10
销售量 2.5 3 4 4.5 6 8 8.5
(1)试根据1月份至5月份的数据,建立关于的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差都不超过0.7万件,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想
参考公式:回归直线方程,其中,.
20.(12分)
已知函数.
(1)求的极值;
(2)若对于任意不同的,,都有,求实数的取值范围.
21.(12分)
已知某工厂的一种机器有两个相同的易损配件,当两个配件都正常工作时(两个配件损坏与否互不影响),该机器才能正常运转.该工厂计划购买一批易损配件,现有甲.乙两个品牌的配件供选择,甲、乙两个品牌的配件可以搭配使用,甲品牌配件的价格为400元/个,乙品牌配件的价格为800元/个.现需决策如何购买易损配件,为此收集并整理了以往购买的甲、乙两个品牌配件各100个的使用时间的数据,得到如下柱状图.分别以甲、乙两种配件使用时间的频率作为概率.
(1)若从2个甲品牌配件和2个乙品牌配件中任选2个装入机器,求该机器正常运转时间不少于2个月的概率.
(2)现有两种购置方案:方案一,购置2个甲品牌配件;方案二,购置2个乙品牌配件.试从性价比(机器正常运转的时间的数学期望与成本的比值)的角度考虑,哪一种方案更实惠
甲品牌配件 乙品牌配件
22.(12分)
已知函数,为的导函数.
(1)讨论的单调性.
(2)当时,证明:.
沧衡八校联盟2021-2022学年高二下学期期中考试
数学试题参考答案
1.B 恰有1瓶是酸牛奶的选取方法有种.
2.A 在上的平均变化率为
3.C 因为,所以
4.D 不同的站法共有种.
5.A 由图可知,当时,;当时,.所以的单调递增区间为和,单调递减区间为.故的极大值点为.
6.D 每人报考大学有3种选择,故总的报考方法共有种,三人所报考的大学均不相同的报考方法有种,甲报考的大学与其他两人均不相同的报考方法有种,故
7.C 对于选项A,例如,从1,2,3,4中随机选出一个数字,记事件为“选出的数字为1或2”,事件为“选出的数字为1或3”,事件为“选出的数字为1或4”,则事件,,,同时发生的事件为“选出的数字为1”,因为,,所以,,,故,,是一组两两独立的事件,但是,A不正确.对于选项B,例如,投掷一枚质地均匀的骰子,记事件为“点数为1,2,3”,事件为“点数为2,4,6”,则,但是,不是对立事件,B不正确.对于选项C,因为,是互斥事件,所以为必然事件,则,C正确.对于选项D,互斥事件不一定是对立事件,对立事件一定是互斥事件,所以“,是互斥事件”是“,是对立事件”的必要不充分条件,D不正确.
8.B 两边求导,得.
令,得,
令,得,
所以.
9.AC 由,得,则.
10.BD 由正态分布密度曲线可知,红茶和绿茶日销量的平均值相等,B不正确.越小,图象越瘦、高,数据越稳定,所以绿茶日销量的稳定性高于红茶日销量的稳定性,A正确.红茶日销量在内的概率约为,C正确.绿茶日销量在内的概率约为,D不正确.
11.ACD 由图可知,从地出发去往地的最短路径共包含7步,其中3步向上,4步向右,且前3步中,至少有1步向上,则不同的路径共有条.若甲途经地,则不同的路径共有条.若甲途经地,且不经过地,则不同的路径共有条.故选ACD.
12.ABC 令函数,则.当时,,在上单调递增,则,即,故,B正确.令函数,则,当时,,在上单调递增,则,故,A,C正确,D不正确.
13. ,令,得,所以.
14. 因为
所以,所以解得,
故
15.300;200 从25人中选出2人,共有种选法,若选出的2人既不在同一行又不在同一列,则共有种选法.
16. 小球最终落人④号球槽,共有5步,其中3步向右,2步向左,故所求概率为
17.解:(1)零假设:瓜子的日销售量与口味无关联.
由题可知,
根据小概率值的独立性检验,我们推断不成立,故认为瓜子的日销售量与口味有关联,此推断犯错误的概率不大于0.05.
(2)由题可知,每公斤原味瓜子的利润为2元,每公斤焦糖味瓜子的利润为3元
设当天焦糖味瓜子的销量为公斤,则,
解得,故当天焦糖味瓜子的最低销量为50公斤.
18.解:(1)因为,所以,
又的图象在处的切线方程为,所以
解得
(2)由(1)可知,,
则当时,;当时,
又,
所以在上的最大值为,最小值为
19.解:(1)因为,
所以,
所以,于是关于的回归直线方程为
(2)当时,,则,
当时,,则,
故可以认为(1)中所得到的回归直线方程是理想的.
20.解:(1)因为,所以
令,解得或(舍去).
当变化时,,的变化情况如表所示.
2
0
单调递减 单调递增
因此,当时,有极小值,且极小值为,无极大值
(2)不妨令,则等价于,即
令函数,可知在上单调递减,
若,即,则在上恒成立,故在上恒成立,
则在上单调递减,符合题意
若,即,则在上不恒成立,故在上不恒成立,则在上不可能单调递减,不符合题意.
综上所述,实数的取值范围为
21.解:(1)若装入2个甲品牌的配件,则该机器正常运转时间不少于2个月的概率为
若装入2个乙品牌的配件,则该机器正常运转时间不少于2个月的概率为
若装入1个甲品牌和1个乙品牌的配件,则该机器正常运转时间不少于2个月的概率为
故该机器正常运转时间不少于2个月的概率为
(2)若采用方案一,设机器可正常运转的时间为(单位:月),则的可能取值为1,2,
且,
所以的分布列为
1 2
,它与购置配件的成本之比为
若采用方案二,设机器可正常运转的时间为(单位:月),则的可能取值为3,4,
且,
所以的分布列为
3 4
,它与购置配件的成本之比为,
因为,所以从性价比的角度考虑,方案二更实惠.
22.(1)解:因为,所以
令函数,则.
若,则在上恒成立.
若,则当时,;
当时,
故当时,在上单调递增;
当时,在上单调递增,在上单调递减.
(2)证明:要证,即证.
当时,,,故.
当时,要证,即证
令函数,则
当时,;当时,.
所以,故要证,只需证
令函数,则
令函数,则,则,即,
所以,所以,即
综上所述,当时,
同课章节目录
