沪科版数学八年级下册 第18章 勾股定理 复习 课件(共40张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 第18章 勾股定理 复习 课件(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 685.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 19:09:08 | ||
图片预览


文档简介
(共40张PPT)
第18章 勾股定理 复习课件
C
A
B
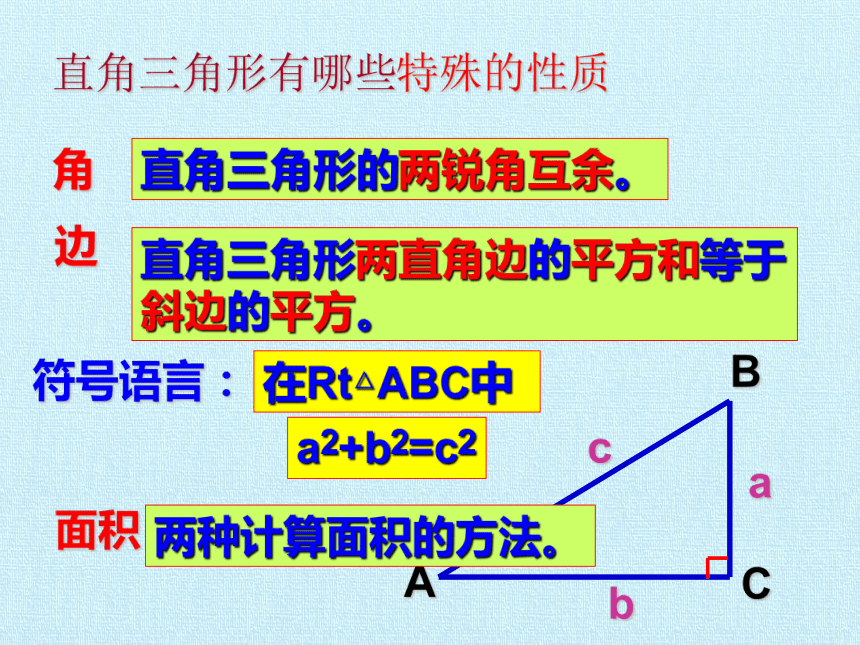
直角三角形有哪些特殊的性质
角
边
面积
直角三角形的两锐角互余。
直角三角形两直角边的平方和等于
斜边的平方。
两种计算面积的方法。
符号语言:
在Rt△ABC中
a2+b2=c2
a
b
c
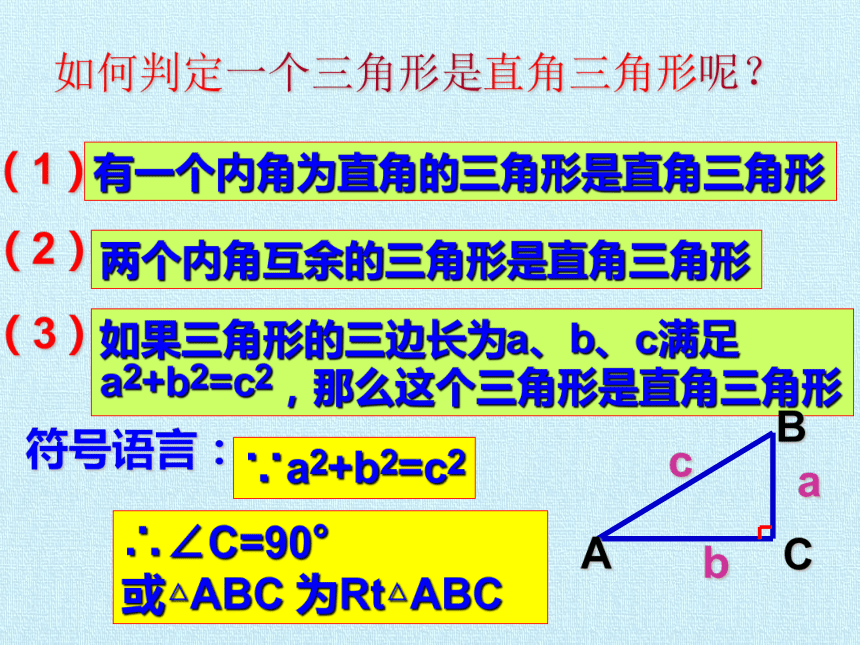
如何判定一个三角形是直角三角形呢?
(1)
(2)
有一个内角为直角的三角形是直角三角形
两个内角互余的三角形是直角三角形
符号语言:
∴∠C=90°
或△ABC 为Rt△ABC
∵a2+b2=c2
(3)
如果三角形的三边长为a、b、c满足
a2+b2=c2,那么这个三角形是直角三角形
C
A
B
a
b
c
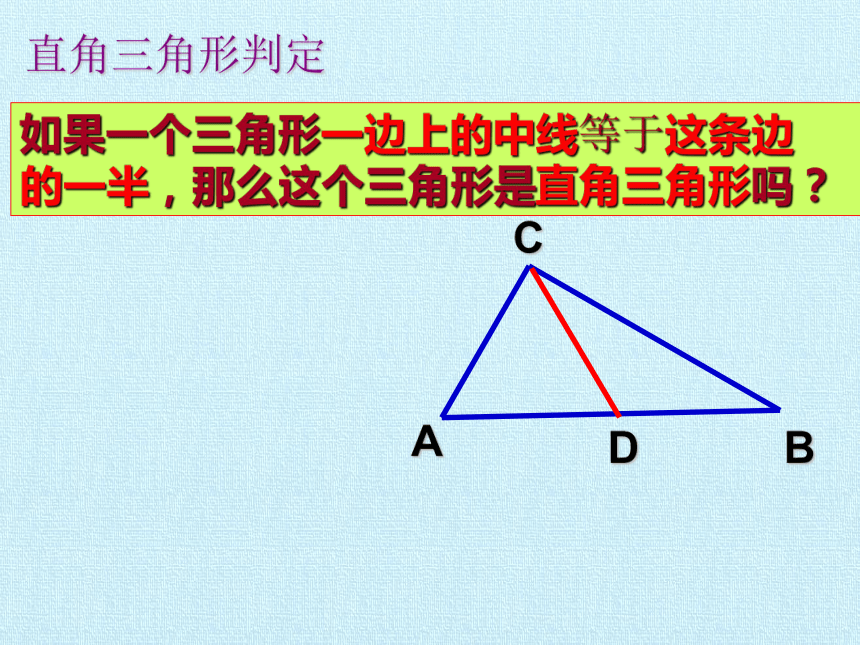
如果一个三角形一边上的中线等于这条边
的一半,那么这个三角形是直角三角形吗?
直角三角形判定
C
A
B
D
C
A
B
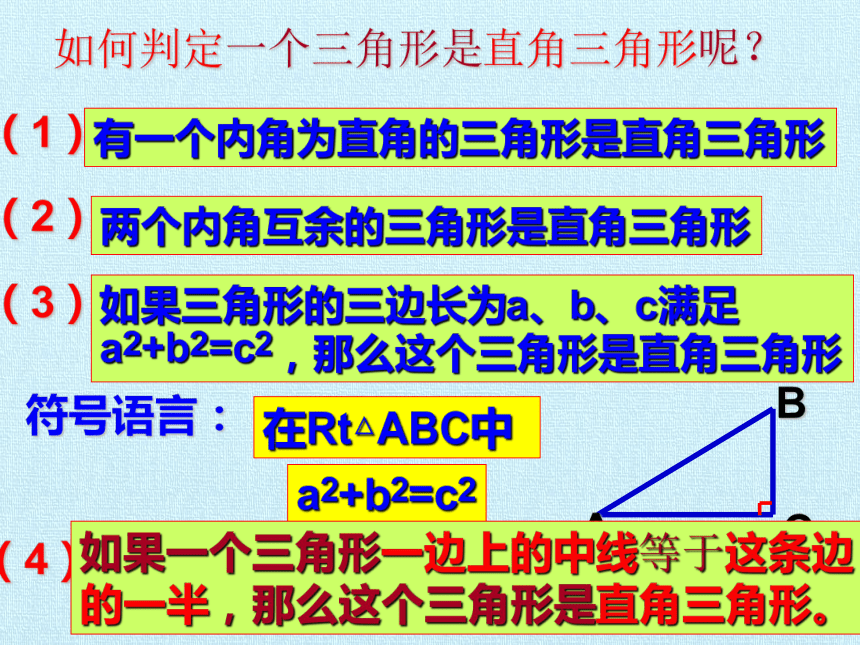
如何判定一个三角形是直角三角形呢?
(1)
(2)
(4)
有一个内角为直角的三角形是直角三角形
两个内角互余的三角形是直角三角形
符号语言:
在Rt△ABC中
a2+b2=c2
(3)
如果三角形的三边长为a、b、c满足
a2+b2=c2,那么这个三角形是直角三角形
如果一个三角形一边上的中线等于这条边
的一半,那么这个三角形是直角三角形。
有四个三角形,分别满足下列条件:
①一个内角等于另两个内角之和;
②三个角之比为3:4:5;
③三边长分别为7、24、25
④三边之比为5:12:13
其中直角三角形有( )
A、1个 B、2个 C、3个 D、4个
C
5
4
3
2
1
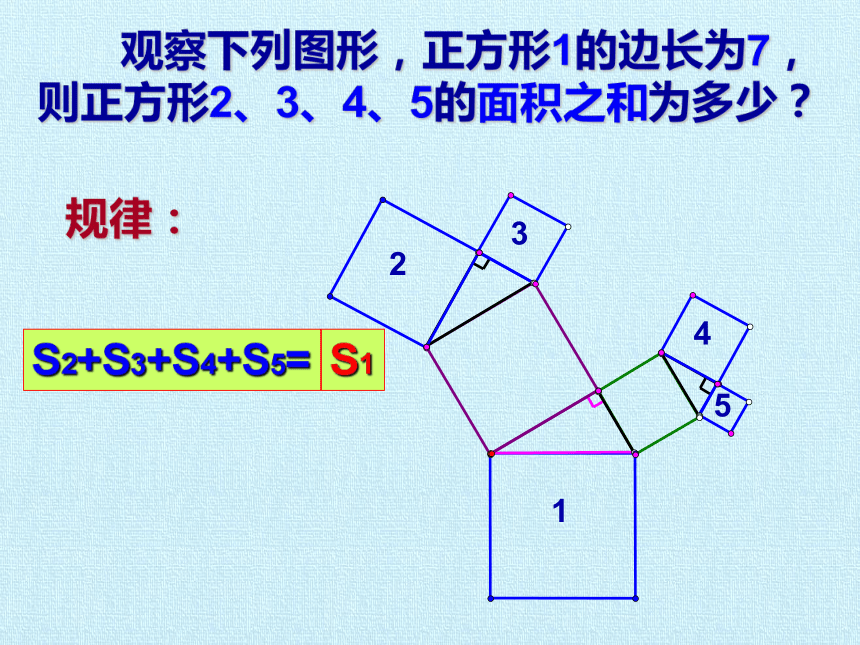
观察下列图形,正方形1的边长为7,则正方形2、3、4、5的面积之和为多少?
规律:
S2+S3+S4+S5=
S1
4′
3′
4
3
2′
2
1
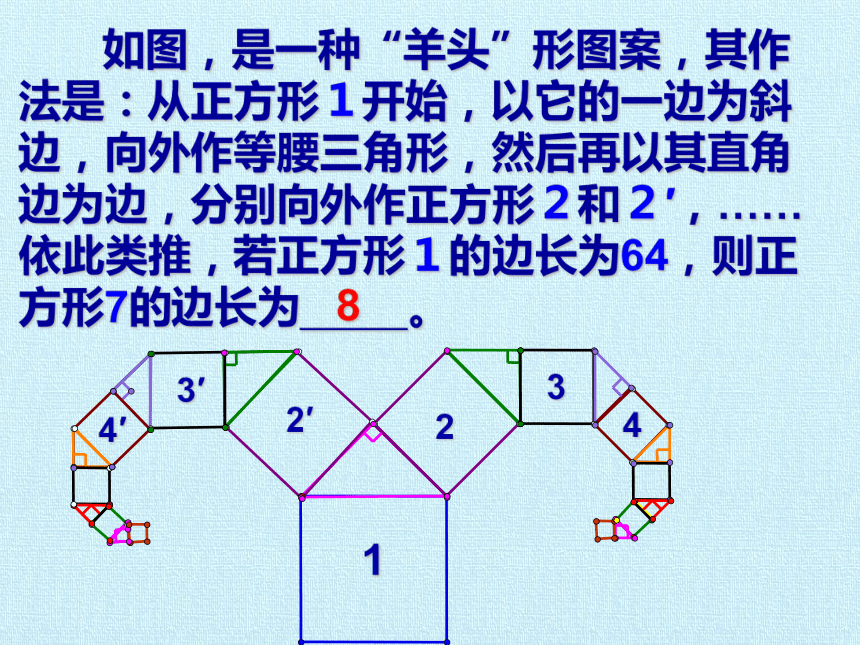
如图,是一种“羊头”形图案,其作法是:从正方形1开始,以它的一边为斜边,向外作等腰三角形,然后再以其直角边为边,分别向外作正方形2和2′,……依此类推,若正方形1的边长为64,则正方形7的边长为 。
8
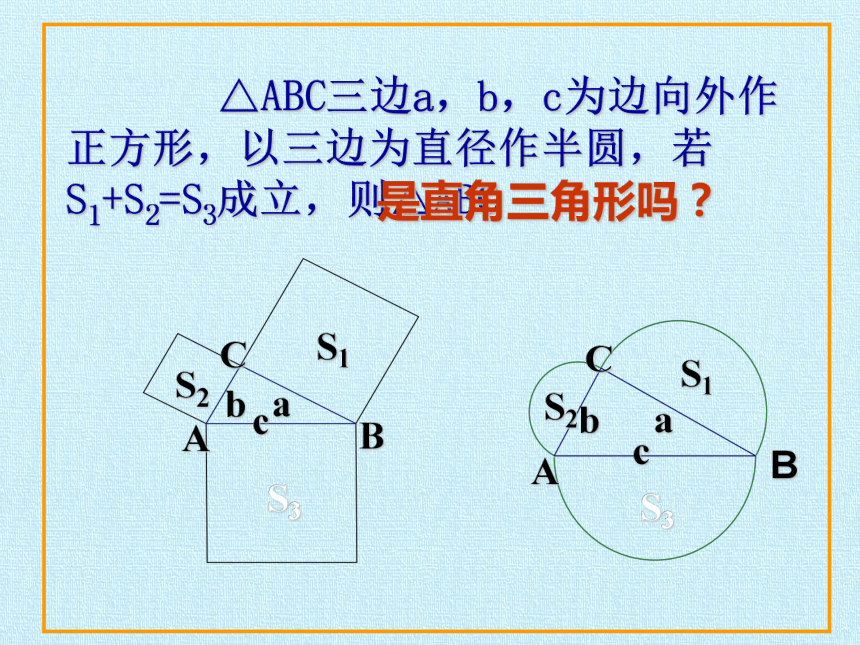
△ABC三边a,b,c为边向外作正方形,以三边为直径作半圆,若S1+S2=S3成立,则△ABC
是直角三角形吗?
A
C
a
b
c
S1
S2
S3
A
B
C
a
b
c
S1
S2
S3
B
S
S
S
C
B
A
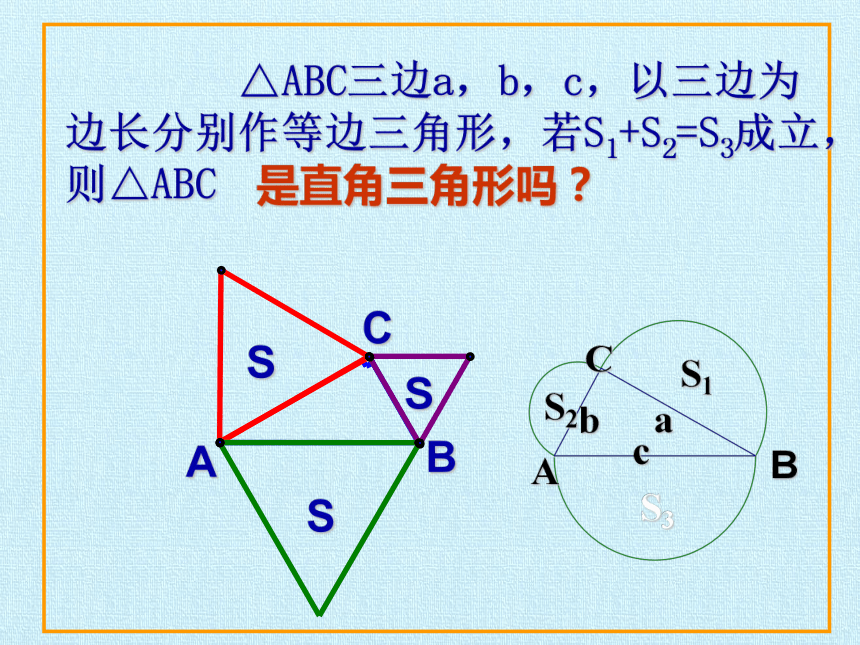
△ABC三边a,b,c,以三边为边长分别作等边三角形,若S1+S2=S3成立,则△ABC
是直角三角形吗?
A
C
a
b
c
S1
S2
S3
B
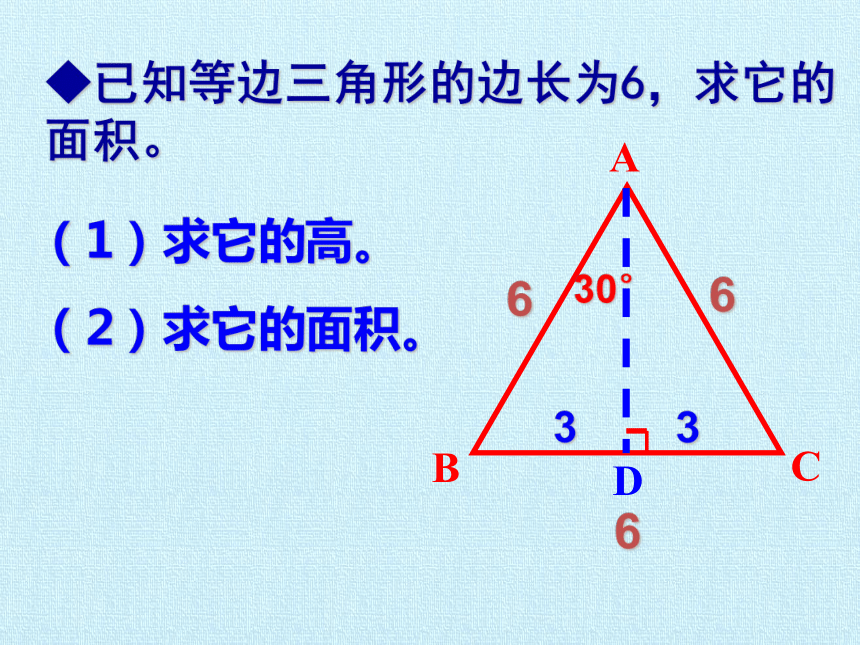
◆已知等边三角形的边长为6,求它的面积。
(1)求它的高。
(2)求它的面积。
B
A
C
D
6
6
6
3
3
30°
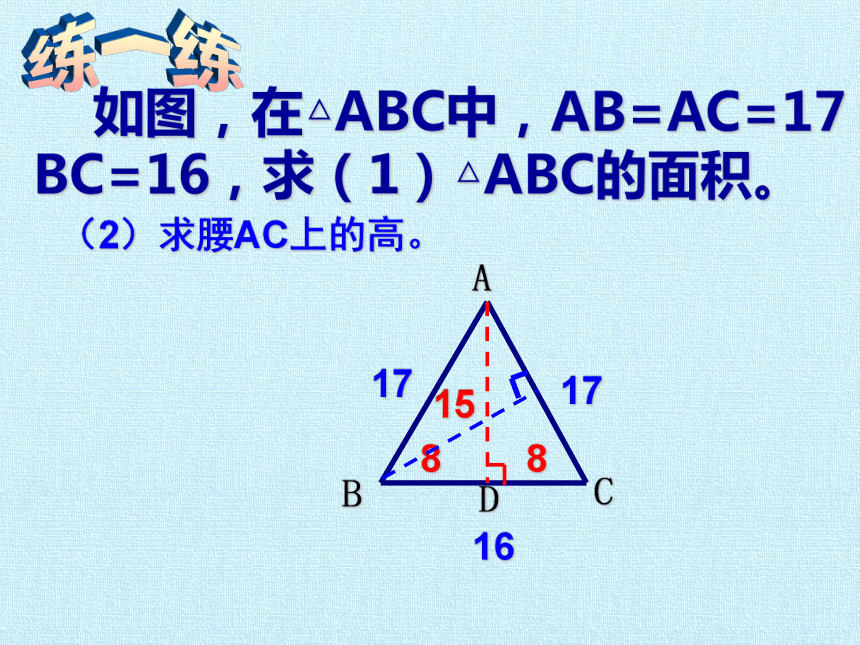
如图,在△ABC中,AB=AC=17,BC=16,求(1)△ABC的面积。
练一练
D
C
B
A
17
17
16
8
8
15
(2)求腰AC上的高。
如图6,在△ABC中,AD⊥BC,AB=15,AD=12,AC=13,求△ABC的周长和面积。
C
B
A
D
15
13
12
9
5
C
80
60
25
24
B
A
如图所示是某机械零件的平面图,尺寸如图所示,求两孔中心A,B之间的距离。(单位:毫米)
如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。AB=9,BC=3,试求以折痕EF为边长的正方形面积。
A
B
C
D
G
F
E
H
9
3
x
9-x
9-x
x2+32=(9-x)2
x=4
9-x=5
解:
5
5
4
1
3
如图,在矩形ABCD中,BC=8,CD=4,将矩形沿BD折叠,点A落在A′处,求重叠部分△BFD的面积。
A
B
C
D
F
A′
4
8
x
8-x
8-x
42+x2=(8-x)2
X=3
S△BFD=5×4÷2=10
8-X=5
3
5
如图,将一根25cm长的细木棍放入长,宽高分别为8cm、6cm、和 cm的长方体无盖盒子中,求细木棍露在外面的最短长度是多少?
A
B
C
D
E
8
6
25
10
20
5
某校A与直线公路距离为3000米,又与该公路的某车站D的距离为5000米,现在要在公路边建一小商店C,使之与该校A及车站D的距离相等,求商店与车站D的距离。
A
B
C
D
3000
5000
4000
x
4000-x
x
3125
A
M
N
P
Q
30°
160
80
E
如图,公路MN和小路PQ在P处交汇,∠QPN=30°,点A处有一所学校,AP=160m,假设拖拉机行使时,周围100m内受噪音影响,那么拖拉机在公路MN上以18km/h的速度沿PN方向行驶时,学校是否受到噪音的影响?如果学校受到影响,那么受影响将持续多长时间?
A
M
N
P
Q
B
D
E
如图,公路MN和小路PQ在P处交汇,∠QPN=30°,点A处有一所学校,AP=160m,假设拖拉机行使时,周围100m内受噪音影响,那么拖拉机在公路MN上以18km/h的速度沿PN方向行驶时,学校是否受到噪音的影响?如果学校受到影响,那么受影响将持续多长时间?
A
M
N
P
Q
30°
B
D
160
80
E
100
60
60
100
如图,公路MN和小路PQ在P处交汇,∠QPN=30°,点A处有一所学校,AP=160m,假设拖拉机行使时,周围100m内受噪音影响,那么拖拉机在公路MN上以18km/h的速度沿PN方向行驶时,学校是否受到噪音的影响?如果学校受到影响,那么受影响将持续多长时间?
有一棵树(如图中的CD)的10m高处B有两只猴子,其中一只猴子爬下树走到离树20m处的池塘A处,另一只猴子爬到树顶D后直接跃向池塘的A处,如果两只猴子所经过的距离相等,试问这棵树多高。
D
B
C
A
10
20
x
30-x
解:设BD=xm
由题意可知,
BC+CA=BD+DA
∴DA=30-x
在Rt△ADC中,
解得x=5
∴树高CD=BC+BD=10+5=15(m)
△ABC中,周长是24,∠C=90°,且AB=9,则三角形的面积是多少?
C
A
B
a
b
c
解:由题意可知,
已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是( )
A.24cm2 B.36cm2 C.48cm2 D.60cm2
C
A
B
a
b
c
a+b=14
c=10
a2+b2=102=100
(a+b)2=142=196
2ab=(a+b)2-(a2+b2)
=196-100
=96
A
等腰三角形底边上的高为8,周长为32,则三角形的面积为( )
A、56 B、48 C、40 D、32
A
B
C
D
8
x
x
16-x
x2+82=(16-x)2
x=6
BC=2x=12
B
如图所示是2002年8月北京第24届国际数学家大会会标“弦图”,它由4个全等的直角三角形拼合而成。如果图中大、小正方形的面积分别为52和4,那么一个直角三角形的两直角边的和等于 。
c2=52
(a-b)2=4
a2+b2=52
a+b=?
a2+b2 -2ab=4
52-2ab=4
ab=24
(a+b)2=a2+b2+2ab=52+48=100
10
正方形面积与勾股定理中的a2、b2、c2的相互转化
在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个的正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4= 。
S1
S2
S3
S4
1
2
3
4
解:设所求直角三角形的斜边为x,另一直角
边为y,则
直角三角形的一条直角边为9,另两边均为自然数,则另两条边分别是多少?
∴(x-y)(x+y)=81
x2-y2=92
∴ x+y>x-y,且x+y,x-y都为自然数
∵x>y
∵81=1×81=3×27=9×9
或
或
如图,∠B=∠C=∠D=∠E=90°,且AB=CD=3,BC=4,DE=EF=2,则求AF的长。
A
B
C
D
E
F
3
3
4
2
2
3
2
4
2
10
C
如图,一条河同一侧的两村庄A、B,其中A、B到河岸最短距离分别为AC=1km,BD=2km,CD=4cm,现欲在河岸上建一个水泵站向A、B两村送水,当建在河岸上何处时,使到A、B两村铺设水管总长度最短,并求出最短距离。
A
P
B
A′
D
E
1
2
4
1
1
4
5
如图所示,正方形ABCD的对角线相交于点O,OE、EF、FG、GH、HM、MN都是垂线,若△AMN的面积等于1cm2,那么,正方形ABCD的边长等于 。
M
N
H
G
F
E
O
D
C
B
A
一辆装满货物的卡车2.5m高,1.6m宽,要开进具有如图所示形状厂门的某工厂,问这辆卡车能否通过厂门?说明你的理由。
2
1
2.3
0.6
0.8
A
B
O
P
Q
为了筹备迎新生晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色泊纸,如图已知圆筒高108cm,其截面周长为36cm,如果在表面缠绕油纸4圈,应截剪多长油纸。
27
36
108
A
B
C
45
45×4=180
如图是一个长8m,宽6m,高5m的仓库,在其内壁的A处(长的四等分点)处有一只壁虎,B(宽的三等分)处有一只蚊子,则壁虎抓到蚊子的最短距离的平方为 m2。
A
B
8
6
5
A
B
8
6
5
6
4
B
A
5
8
6
6
4
A
B
A
B
8
6
5
8
5
5
6
6
4
如图是一个长8m,宽6m,高5m的仓库,在其内壁的A处(长的四等分点)处有一只壁虎,B(宽的三等分)处有一只蚊子,则壁虎抓到蚊子的最短距离的平方为 m2。
甲乙两人在沙漠进行探险,某日早晨8:00甲先出发,他以6千米/时速度向东南方向行走,1小时后乙出发,他以5千米/时速度向西南方向行走,上午10:00时,甲乙两人相距多远?
北
南
西
东
甲
乙
解:甲走的路程:
乙走的路程:
甲、乙两人之间的距离:
6×(10-8)=12 (千米)
5×(10-9)=5 (千米)
西宁市风景区有2个景点A、B(B位于A的正东方),为了方便游客,风景区管理处决定在相距2千米的A、B两景点之间修一条笔直的公路(即图中的线段AB),经测量,在点A的北偏东60°方向、点B的北偏西45°方向的C处有一个半径为0.7千米的小水潭,问小水潭会不会影响公路的修筑,为什么?
参考数据:
C
A
B
D
60°
45°
30°
45°
x
x
如图,已知:等腰直角△ABC中,P为斜边BC上的任一点。求证:PB2+PC2=2PA2。
A
B
C
P
D
直角三角形两直角边长为a、b,斜边上的高为h,则下列各式总能成立的是( )
A、ab=h2 B、a2+b2=2h2
C、 D、
D
谢 谢
第18章 勾股定理 复习课件
C
A
B
直角三角形有哪些特殊的性质
角
边
面积
直角三角形的两锐角互余。
直角三角形两直角边的平方和等于
斜边的平方。
两种计算面积的方法。
符号语言:
在Rt△ABC中
a2+b2=c2
a
b
c
如何判定一个三角形是直角三角形呢?
(1)
(2)
有一个内角为直角的三角形是直角三角形
两个内角互余的三角形是直角三角形
符号语言:
∴∠C=90°
或△ABC 为Rt△ABC
∵a2+b2=c2
(3)
如果三角形的三边长为a、b、c满足
a2+b2=c2,那么这个三角形是直角三角形
C
A
B
a
b
c
如果一个三角形一边上的中线等于这条边
的一半,那么这个三角形是直角三角形吗?
直角三角形判定
C
A
B
D
C
A
B
如何判定一个三角形是直角三角形呢?
(1)
(2)
(4)
有一个内角为直角的三角形是直角三角形
两个内角互余的三角形是直角三角形
符号语言:
在Rt△ABC中
a2+b2=c2
(3)
如果三角形的三边长为a、b、c满足
a2+b2=c2,那么这个三角形是直角三角形
如果一个三角形一边上的中线等于这条边
的一半,那么这个三角形是直角三角形。
有四个三角形,分别满足下列条件:
①一个内角等于另两个内角之和;
②三个角之比为3:4:5;
③三边长分别为7、24、25
④三边之比为5:12:13
其中直角三角形有( )
A、1个 B、2个 C、3个 D、4个
C
5
4
3
2
1
观察下列图形,正方形1的边长为7,则正方形2、3、4、5的面积之和为多少?
规律:
S2+S3+S4+S5=
S1
4′
3′
4
3
2′
2
1
如图,是一种“羊头”形图案,其作法是:从正方形1开始,以它的一边为斜边,向外作等腰三角形,然后再以其直角边为边,分别向外作正方形2和2′,……依此类推,若正方形1的边长为64,则正方形7的边长为 。
8
△ABC三边a,b,c为边向外作正方形,以三边为直径作半圆,若S1+S2=S3成立,则△ABC
是直角三角形吗?
A
C
a
b
c
S1
S2
S3
A
B
C
a
b
c
S1
S2
S3
B
S
S
S
C
B
A
△ABC三边a,b,c,以三边为边长分别作等边三角形,若S1+S2=S3成立,则△ABC
是直角三角形吗?
A
C
a
b
c
S1
S2
S3
B
◆已知等边三角形的边长为6,求它的面积。
(1)求它的高。
(2)求它的面积。
B
A
C
D
6
6
6
3
3
30°
如图,在△ABC中,AB=AC=17,BC=16,求(1)△ABC的面积。
练一练
D
C
B
A
17
17
16
8
8
15
(2)求腰AC上的高。
如图6,在△ABC中,AD⊥BC,AB=15,AD=12,AC=13,求△ABC的周长和面积。
C
B
A
D
15
13
12
9
5
C
80
60
25
24
B
A
如图所示是某机械零件的平面图,尺寸如图所示,求两孔中心A,B之间的距离。(单位:毫米)
如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。AB=9,BC=3,试求以折痕EF为边长的正方形面积。
A
B
C
D
G
F
E
H
9
3
x
9-x
9-x
x2+32=(9-x)2
x=4
9-x=5
解:
5
5
4
1
3
如图,在矩形ABCD中,BC=8,CD=4,将矩形沿BD折叠,点A落在A′处,求重叠部分△BFD的面积。
A
B
C
D
F
A′
4
8
x
8-x
8-x
42+x2=(8-x)2
X=3
S△BFD=5×4÷2=10
8-X=5
3
5
如图,将一根25cm长的细木棍放入长,宽高分别为8cm、6cm、和 cm的长方体无盖盒子中,求细木棍露在外面的最短长度是多少?
A
B
C
D
E
8
6
25
10
20
5
某校A与直线公路距离为3000米,又与该公路的某车站D的距离为5000米,现在要在公路边建一小商店C,使之与该校A及车站D的距离相等,求商店与车站D的距离。
A
B
C
D
3000
5000
4000
x
4000-x
x
3125
A
M
N
P
Q
30°
160
80
E
如图,公路MN和小路PQ在P处交汇,∠QPN=30°,点A处有一所学校,AP=160m,假设拖拉机行使时,周围100m内受噪音影响,那么拖拉机在公路MN上以18km/h的速度沿PN方向行驶时,学校是否受到噪音的影响?如果学校受到影响,那么受影响将持续多长时间?
A
M
N
P
Q
B
D
E
如图,公路MN和小路PQ在P处交汇,∠QPN=30°,点A处有一所学校,AP=160m,假设拖拉机行使时,周围100m内受噪音影响,那么拖拉机在公路MN上以18km/h的速度沿PN方向行驶时,学校是否受到噪音的影响?如果学校受到影响,那么受影响将持续多长时间?
A
M
N
P
Q
30°
B
D
160
80
E
100
60
60
100
如图,公路MN和小路PQ在P处交汇,∠QPN=30°,点A处有一所学校,AP=160m,假设拖拉机行使时,周围100m内受噪音影响,那么拖拉机在公路MN上以18km/h的速度沿PN方向行驶时,学校是否受到噪音的影响?如果学校受到影响,那么受影响将持续多长时间?
有一棵树(如图中的CD)的10m高处B有两只猴子,其中一只猴子爬下树走到离树20m处的池塘A处,另一只猴子爬到树顶D后直接跃向池塘的A处,如果两只猴子所经过的距离相等,试问这棵树多高。
D
B
C
A
10
20
x
30-x
解:设BD=xm
由题意可知,
BC+CA=BD+DA
∴DA=30-x
在Rt△ADC中,
解得x=5
∴树高CD=BC+BD=10+5=15(m)
△ABC中,周长是24,∠C=90°,且AB=9,则三角形的面积是多少?
C
A
B
a
b
c
解:由题意可知,
已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是( )
A.24cm2 B.36cm2 C.48cm2 D.60cm2
C
A
B
a
b
c
a+b=14
c=10
a2+b2=102=100
(a+b)2=142=196
2ab=(a+b)2-(a2+b2)
=196-100
=96
A
等腰三角形底边上的高为8,周长为32,则三角形的面积为( )
A、56 B、48 C、40 D、32
A
B
C
D
8
x
x
16-x
x2+82=(16-x)2
x=6
BC=2x=12
B
如图所示是2002年8月北京第24届国际数学家大会会标“弦图”,它由4个全等的直角三角形拼合而成。如果图中大、小正方形的面积分别为52和4,那么一个直角三角形的两直角边的和等于 。
c2=52
(a-b)2=4
a2+b2=52
a+b=?
a2+b2 -2ab=4
52-2ab=4
ab=24
(a+b)2=a2+b2+2ab=52+48=100
10
正方形面积与勾股定理中的a2、b2、c2的相互转化
在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个的正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4= 。
S1
S2
S3
S4
1
2
3
4
解:设所求直角三角形的斜边为x,另一直角
边为y,则
直角三角形的一条直角边为9,另两边均为自然数,则另两条边分别是多少?
∴(x-y)(x+y)=81
x2-y2=92
∴ x+y>x-y,且x+y,x-y都为自然数
∵x>y
∵81=1×81=3×27=9×9
或
或
如图,∠B=∠C=∠D=∠E=90°,且AB=CD=3,BC=4,DE=EF=2,则求AF的长。
A
B
C
D
E
F
3
3
4
2
2
3
2
4
2
10
C
如图,一条河同一侧的两村庄A、B,其中A、B到河岸最短距离分别为AC=1km,BD=2km,CD=4cm,现欲在河岸上建一个水泵站向A、B两村送水,当建在河岸上何处时,使到A、B两村铺设水管总长度最短,并求出最短距离。
A
P
B
A′
D
E
1
2
4
1
1
4
5
如图所示,正方形ABCD的对角线相交于点O,OE、EF、FG、GH、HM、MN都是垂线,若△AMN的面积等于1cm2,那么,正方形ABCD的边长等于 。
M
N
H
G
F
E
O
D
C
B
A
一辆装满货物的卡车2.5m高,1.6m宽,要开进具有如图所示形状厂门的某工厂,问这辆卡车能否通过厂门?说明你的理由。
2
1
2.3
0.6
0.8
A
B
O
P
Q
为了筹备迎新生晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色泊纸,如图已知圆筒高108cm,其截面周长为36cm,如果在表面缠绕油纸4圈,应截剪多长油纸。
27
36
108
A
B
C
45
45×4=180
如图是一个长8m,宽6m,高5m的仓库,在其内壁的A处(长的四等分点)处有一只壁虎,B(宽的三等分)处有一只蚊子,则壁虎抓到蚊子的最短距离的平方为 m2。
A
B
8
6
5
A
B
8
6
5
6
4
B
A
5
8
6
6
4
A
B
A
B
8
6
5
8
5
5
6
6
4
如图是一个长8m,宽6m,高5m的仓库,在其内壁的A处(长的四等分点)处有一只壁虎,B(宽的三等分)处有一只蚊子,则壁虎抓到蚊子的最短距离的平方为 m2。
甲乙两人在沙漠进行探险,某日早晨8:00甲先出发,他以6千米/时速度向东南方向行走,1小时后乙出发,他以5千米/时速度向西南方向行走,上午10:00时,甲乙两人相距多远?
北
南
西
东
甲
乙
解:甲走的路程:
乙走的路程:
甲、乙两人之间的距离:
6×(10-8)=12 (千米)
5×(10-9)=5 (千米)
西宁市风景区有2个景点A、B(B位于A的正东方),为了方便游客,风景区管理处决定在相距2千米的A、B两景点之间修一条笔直的公路(即图中的线段AB),经测量,在点A的北偏东60°方向、点B的北偏西45°方向的C处有一个半径为0.7千米的小水潭,问小水潭会不会影响公路的修筑,为什么?
参考数据:
C
A
B
D
60°
45°
30°
45°
x
x
如图,已知:等腰直角△ABC中,P为斜边BC上的任一点。求证:PB2+PC2=2PA2。
A
B
C
P
D
直角三角形两直角边长为a、b,斜边上的高为h,则下列各式总能成立的是( )
A、ab=h2 B、a2+b2=2h2
C、 D、
D
谢 谢
