沪科版数学八年级下册 19.3矩形、菱形、正方形-正方形课件(共15张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 19.3矩形、菱形、正方形-正方形课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 151.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
正方形
矩形、菱形、正方形
操作
1.怎样用一张矩形的纸片折出一个正方形?
2.怎样将一个菱形的木框变成一个正方形的木框?
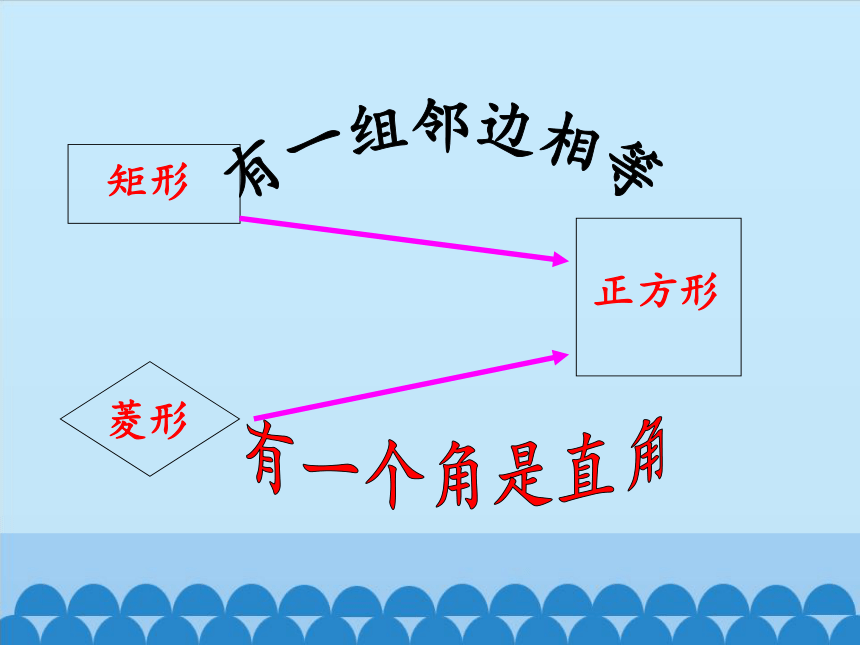
矩形
菱形
正方形
有一组邻边相等
有一个角是直角
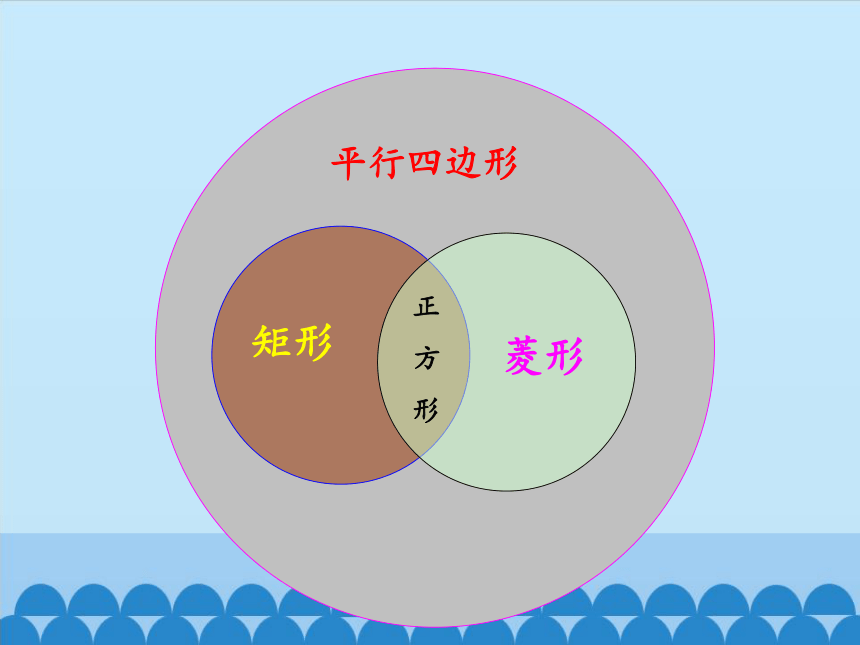
平行四边形
矩形
菱形
正
方
形
讨论
㈠正方形的边、角、对角线各具有什么性质?
边:对边平行,四条边都相等。
角:四个角都相等,都等于90°。
对角线:相等、垂直且互相平分,每一条对角线平分一组对角。
讨论
㈡具备什么条件的平行四边形是正方形?
1.先说明它是矩形,再说明这个矩形有一组邻边相等。
2.先说明它是菱形,再说明这个菱形有一个角是直角。
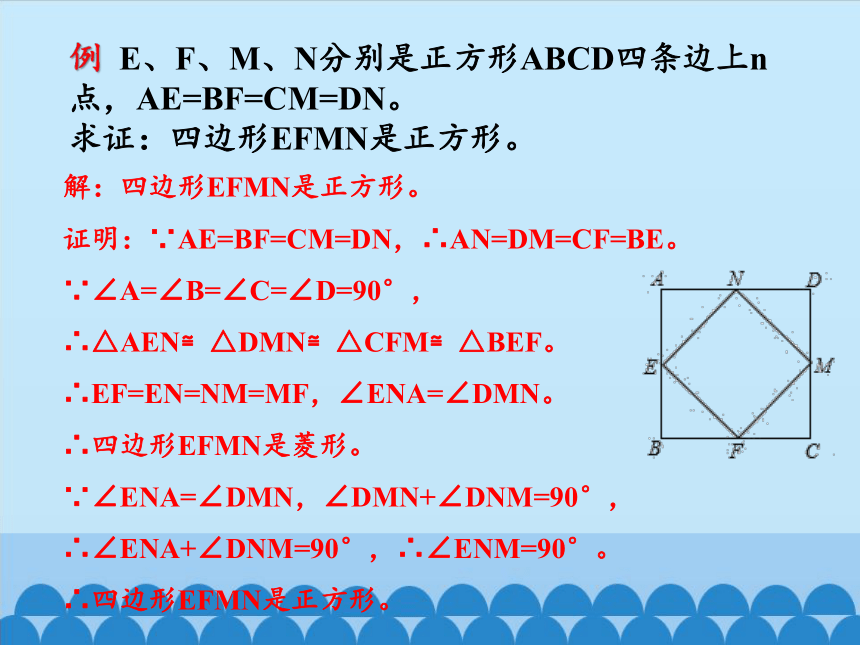
例 E、F、M、N分别是正方形ABCD四条边上n点,AE=BF=CM=DN。
求证:四边形EFMN是正方形。
解:四边形EFMN是正方形。
证明:∵AE=BF=CM=DN,∴AN=DM=CF=BE。
∵∠A=∠B=∠C=∠D=90°,
∴△AEN≌△DMN≌△CFM≌△BEF。
∴EF=EN=NM=MF,∠ENA=∠DMN。
∴四边形EFMN是菱形。
∵∠ENA=∠DMN,∠DMN+∠DNM=90°,
∴∠ENA+∠DNM=90°,∴∠ENM=90°。
∴四边形EFMN是正方形。
想一想
在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想。
G
F
E
D
A
B
C
一展身手
1.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是( )
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
2.在正方形ABCD中,对角线AC、BD相交于点O,点Q是CD上任意一点,DP⊥AQ交BC于点P。
⑴求证:DQ=CP;
⑵OP与OQ有何关系?试证明你的结论。
3.如图,以△ABC的边AB、AC向形外作正方形ABDE和ACFG,M是BC的中点。
求证:
⑴CE=BG;
⑵EG=2AM。
H
M
E
D
F
G
B
C
A
4.求证:矩形的四个角的平分线所围成的四边形是正方形。
思考
▲正方形有哪些性质?如何判别一个平行四边形是正方形?
★从角上来谈;
●从边上来谈;
▲从对角线上来谈。
正方形的定义、性质及判定。
课堂小结
谢 谢
正方形
矩形、菱形、正方形
操作
1.怎样用一张矩形的纸片折出一个正方形?
2.怎样将一个菱形的木框变成一个正方形的木框?
矩形
菱形
正方形
有一组邻边相等
有一个角是直角
平行四边形
矩形
菱形
正
方
形
讨论
㈠正方形的边、角、对角线各具有什么性质?
边:对边平行,四条边都相等。
角:四个角都相等,都等于90°。
对角线:相等、垂直且互相平分,每一条对角线平分一组对角。
讨论
㈡具备什么条件的平行四边形是正方形?
1.先说明它是矩形,再说明这个矩形有一组邻边相等。
2.先说明它是菱形,再说明这个菱形有一个角是直角。
例 E、F、M、N分别是正方形ABCD四条边上n点,AE=BF=CM=DN。
求证:四边形EFMN是正方形。
解:四边形EFMN是正方形。
证明:∵AE=BF=CM=DN,∴AN=DM=CF=BE。
∵∠A=∠B=∠C=∠D=90°,
∴△AEN≌△DMN≌△CFM≌△BEF。
∴EF=EN=NM=MF,∠ENA=∠DMN。
∴四边形EFMN是菱形。
∵∠ENA=∠DMN,∠DMN+∠DNM=90°,
∴∠ENA+∠DNM=90°,∴∠ENM=90°。
∴四边形EFMN是正方形。
想一想
在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想。
G
F
E
D
A
B
C
一展身手
1.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是( )
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
2.在正方形ABCD中,对角线AC、BD相交于点O,点Q是CD上任意一点,DP⊥AQ交BC于点P。
⑴求证:DQ=CP;
⑵OP与OQ有何关系?试证明你的结论。
3.如图,以△ABC的边AB、AC向形外作正方形ABDE和ACFG,M是BC的中点。
求证:
⑴CE=BG;
⑵EG=2AM。
H
M
E
D
F
G
B
C
A
4.求证:矩形的四个角的平分线所围成的四边形是正方形。
思考
▲正方形有哪些性质?如何判别一个平行四边形是正方形?
★从角上来谈;
●从边上来谈;
▲从对角线上来谈。
正方形的定义、性质及判定。
课堂小结
谢 谢
