1 功与功率课件(用)(共34张ppt)
文档属性
| 名称 | 1 功与功率课件(用)(共34张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-26 00:00:00 | ||
图片预览








文档简介
(共34张PPT)
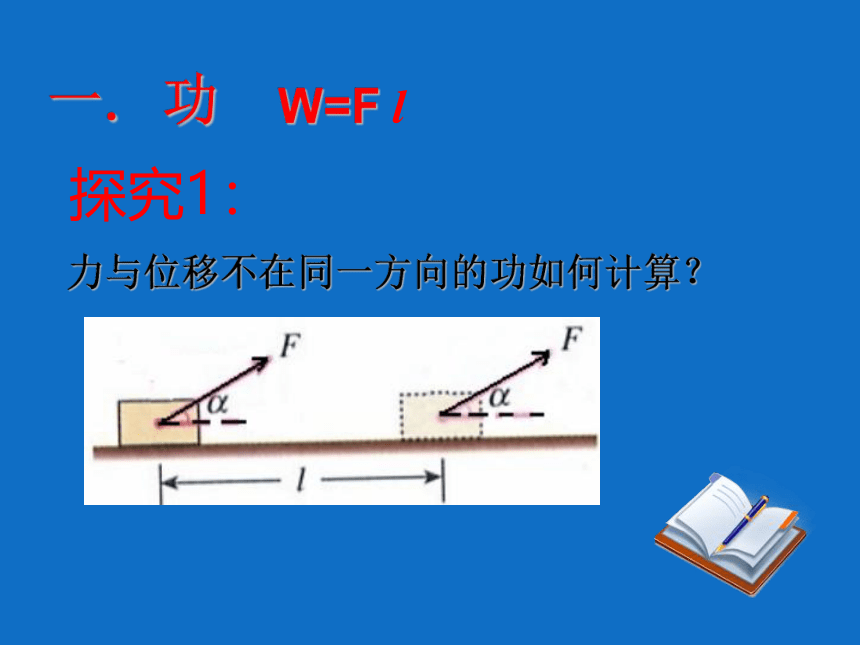
一. 功
W=F l
探究1:
力与位移不在同一方向的功如何计算?
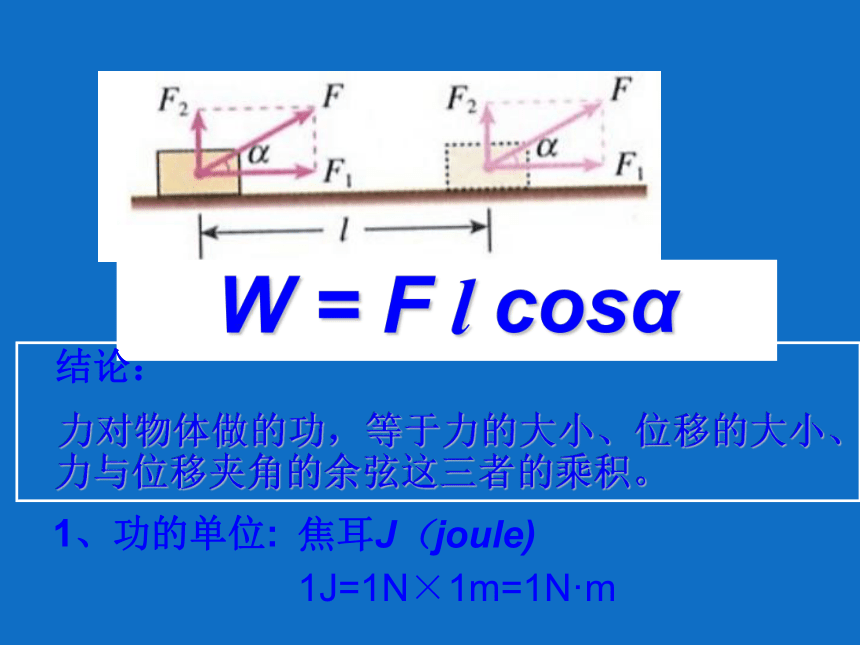
W = F l cosα
结论:
力对物体做的功,等于力的大小、位移的大小、力与位移夹角的余弦这三者的乘积。
1、功的单位:
焦耳J(joule)
1J=1N×1m=1N·m
c、与物体是否受其他力无关,与物体的运动状态无关
a、力必须是恒力;
3、理解:
2、功是标量
只有大小,没有方向
b、公式中的F和l必须具备同时性, l是力的作用对象的对地位移;
W = F l cosα
探究2:
表达式W = F l cosα,由α情况同学们对功有哪些认识?
二、正功和负功:
当
时,cosα=0,W=0,
当
时,cosα>0,W>0,
当
力F对物体做负功。
力F对物体不做功。
力F对物体做正功。
时,cosα<0,W<0,
v
F
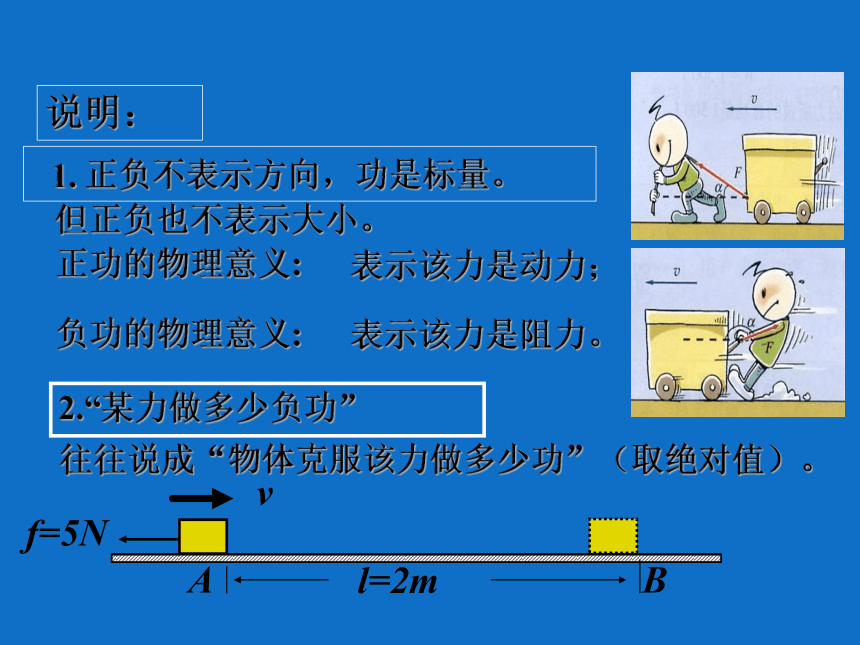
1. 正负不表示方向,功是标量。
负功的物理意义:
正功的物理意义:
表示该力是动力;
表示该力是阻力。
2.“某力做多少负功”
往往说成“物体克服该力做多少功”(取绝对值)。
说明:
v
f=5N
l=2m
A
B
但正负也不表示大小。
三、总功的计算
1、几个力对物体所做的总功等于各个 力对物体所做功的代数和。
W总=W1+W2+……Wn
2、几个力对物体所做的总功等于合外力对物体做功。
W总=F合· l cosα
书中例题1:
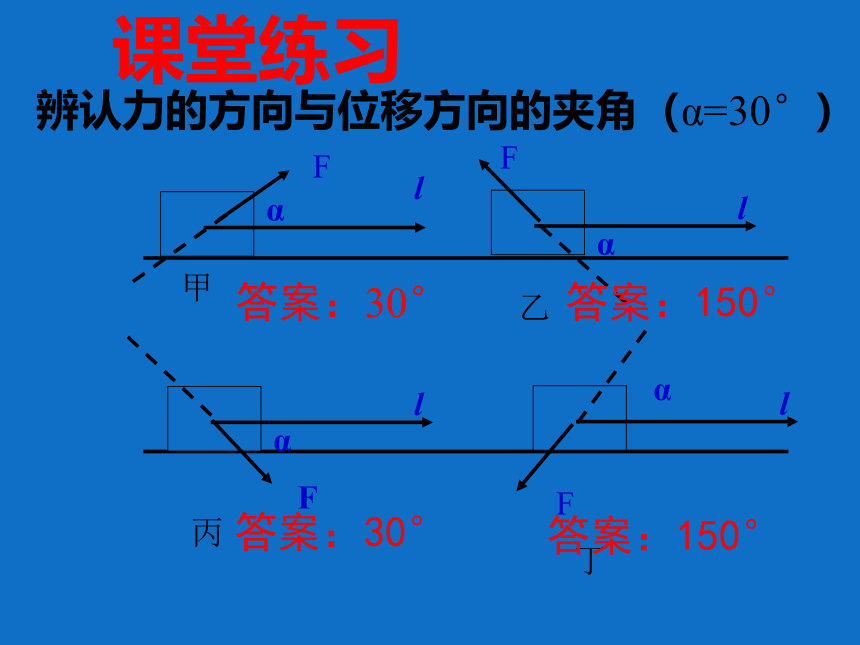
辨认力的方向与位移方向的夹角(α=30°)
α
F
l
甲
答案:30°
α
F
l
乙
答案:150°
α
F
l
丙
答案:30°
α
F
l
丁
答案:150°
课堂练习
用一水平恒力F将木块沿水平方向从A点拉到B点。第一次在光滑水平面上,F所做的功为W1;第二次在粗糙水平面上,F所做的功为W2,比较两次做功,应该( )
A.W1C.W1>W2 D.无法比较
B
A
B
F
力对物体做的功只与F、 l 、 α三者有关,与物体的运动状态等因素无关
一学生用100N的力将质量为0.5kg的球迅速踢出,球在水平路面上滚出20m远,则该学生对球做的功是:( )
A、2000J B、1000J
C、16J D、无法确定
D
要点: 公式中F为恒力,且F、L必须具有同时性。
1.A、B两物体叠放在水平面上,力F拉B物体,保持相对静止一起向右做匀加速运动移动s, 则B对A摩擦力做————功,A对B摩擦力做———功。
A
B
f1
f2
W1=f s W2= - f s W1 + W2= 0
正
负
F
2.A、B两物体叠放在水平面上,A物体用线系在墙上,B 物体在力 F作用下向右运动,则B对A摩擦力做————功,A对B摩擦力做————功。
F
B
A
f1
f2
0
负
3.A、B两物体叠放在水平面上,A物体在力 F作用下在B物体上相对滑动,则B对A的摩擦力做————功,A对B做————功。
A
B
F
f1
f2
ΔS
S2
S1
W1= - fS1
W2= fS2
W1 + W2= f(S2 - S1 )= - f Δ S
负
正
作用力与反作用力做功没有必然关系
1、物理意义:是表示力对物体做功快慢的物理量。
3、公式:
比值定义法
4、功率是标量。
5、功率的单位:
瓦特(W)常用单位: kW
四、功率
2、定义:功W跟完成这些功所用时间t的比值
说明:即使是同一个力做功,做功的功率也可能是变化的,在一段时间内力对物体做功的功率,实际上是这段时间内力对物体做功的平均功率。
平均功率:描述一段时间内做功的平均快慢
瞬时功率:表示在某一时刻做功的快慢
P=
t
W
当 t 很短很短时,此式表示瞬时功率
当 t 表示一段时间时,此式表示平均功率
平均功率和瞬时功率
功率与速度的关系
P=Fv
W=Fscosα
P=
t
W
P=Fvcosα
若力与速度不再一条直线上呢?
功率与速度的关系
P=F v cosα
若v表示瞬时速度,则P 表示瞬时功率
若 v表示平均速度,则P 表示平均功率
对于公式 P = F v
1、当P 一定时,F 和 v 有什么关系?
2、当F 一定时,P 和 v 有什么关系?
3、当v 一定时,F 和 P 有什么关系?
当F与v同方向时(α=0),P=Fv
例题2
注意:汽车的功率就是汽车牵引力的功率
P=F v
发动机的实际功率
发动机的牵引力
机车的瞬时速度
类型1:机车以恒定功率 P 启动
机车启动问题
P=F v
发动机的实际功率
发动机的牵引力
机车的瞬时速度
当F=F阻时,
a=0 ,v达到最大
保持
vm
匀速
v
F=
v
P
a=
m
F-F阻
↑
→
↓
↑
→
→
↓
↓
vm=
F阻
P
加速度逐渐减小的变加速直线运动
匀速直线运动
vm
机车以恒定功率启动的v- t 图
机车启动问题
先做加速度逐渐减小的变加速直线运动,最终以速度 做匀速直线运动。
vm=
F阻
P
v
t
0
类型2:机车以恒定加速度 a 启动
当F= F阻时,
a=0 ,v达到最大
保持
vm
匀速
F=
v
P额
a=
m
F-F阻
↑
→
↓
v
↑
↓
→
→
↓
vm=
F阻
P额
加速度逐渐减小的变加速直线运动
匀速直线运动
a=
m
F-F阻
→
→
→
→
F
→
v
↑
P=F v
↑
↑
→
当P= P额时,保持P额继续加速
匀加速直线运动
机车以恒定加速度启动的v- t 图
先做匀加速直线运动,再做加速度逐渐减小的变加速直线运动,最终以速度 做匀速直线运动。
v
t
0
vm=
F阻
P额
vm
光滑水平面上的物块在弹簧弹力作用下从A点运动到B点,思考能否用W=Fl求弹簧弹力对物体所做的功?
思考:
A
B
对于变力做功不能直接套用公式
求解,但可依物理规律通过技巧的转化,将变力做功转化为恒力做功间接求解。
1.平均力法:
若变力大小随位移是线性变化,且方向不变时,可将变力的平均值求出后用公式
计算。如弹簧的弹力做功就可以用此法计算。
四、变力做功
2.利用F-x图像,F-x图线与坐标轴所包围的面
积即是力F做功的数值。
4.转换研究对象法(等效转换法)
5.用动能定理或能量守恒进行求解:
3. 无限分小法(微元法)来求, 过程无限分小后, 可认为每小段是恒力做功。
例1.一辆马车在力F的作用下绕半径为50 m的圆形轨道做匀速圆周运动,已知车子所受阻力为100N,当车运动一周回到原位置时,车子克服阻力所做的功为多少?
解:阻力的方向时刻在变,是变力做功的问题,不能直接由功的公式计算。
采用微元法解之,将圆分成很多很多小段,在这些小段中,力可以看作恒力,于是
Wf = – fΔs1 – fΔs2 – fΔs3 – fΔs4 – fΔs5 – ……
= – fs= – Fs = – 100×2πR= – 3.14 ×104 J
W克= – Wf= 3.14 ×104 J
解二:用图像法
因为阻力F=kx,以F为纵坐标,F方向上的位移x为横坐标,作出F-x图像,如图右下图,
X
F
0
x1
x2
kx1
kx2
曲线下面积的值等于F对铁钉做的功. (示功图)?
由于两次做功相等,故有:?
S1 = S2 (面积),即:
1/2× kx12=1/2× k(x2+x1)(x2-x1),
解后有:x2= x1=1.41 cm.
∴ △x=x2-x1=0.41 cm.
一. 功
W=F l
探究1:
力与位移不在同一方向的功如何计算?
W = F l cosα
结论:
力对物体做的功,等于力的大小、位移的大小、力与位移夹角的余弦这三者的乘积。
1、功的单位:
焦耳J(joule)
1J=1N×1m=1N·m
c、与物体是否受其他力无关,与物体的运动状态无关
a、力必须是恒力;
3、理解:
2、功是标量
只有大小,没有方向
b、公式中的F和l必须具备同时性, l是力的作用对象的对地位移;
W = F l cosα
探究2:
表达式W = F l cosα,由α情况同学们对功有哪些认识?
二、正功和负功:
当
时,cosα=0,W=0,
当
时,cosα>0,W>0,
当
力F对物体做负功。
力F对物体不做功。
力F对物体做正功。
时,cosα<0,W<0,
v
F
1. 正负不表示方向,功是标量。
负功的物理意义:
正功的物理意义:
表示该力是动力;
表示该力是阻力。
2.“某力做多少负功”
往往说成“物体克服该力做多少功”(取绝对值)。
说明:
v
f=5N
l=2m
A
B
但正负也不表示大小。
三、总功的计算
1、几个力对物体所做的总功等于各个 力对物体所做功的代数和。
W总=W1+W2+……Wn
2、几个力对物体所做的总功等于合外力对物体做功。
W总=F合· l cosα
书中例题1:
辨认力的方向与位移方向的夹角(α=30°)
α
F
l
甲
答案:30°
α
F
l
乙
答案:150°
α
F
l
丙
答案:30°
α
F
l
丁
答案:150°
课堂练习
用一水平恒力F将木块沿水平方向从A点拉到B点。第一次在光滑水平面上,F所做的功为W1;第二次在粗糙水平面上,F所做的功为W2,比较两次做功,应该( )
A.W1
B
A
B
F
力对物体做的功只与F、 l 、 α三者有关,与物体的运动状态等因素无关
一学生用100N的力将质量为0.5kg的球迅速踢出,球在水平路面上滚出20m远,则该学生对球做的功是:( )
A、2000J B、1000J
C、16J D、无法确定
D
要点: 公式中F为恒力,且F、L必须具有同时性。
1.A、B两物体叠放在水平面上,力F拉B物体,保持相对静止一起向右做匀加速运动移动s, 则B对A摩擦力做————功,A对B摩擦力做———功。
A
B
f1
f2
W1=f s W2= - f s W1 + W2= 0
正
负
F
2.A、B两物体叠放在水平面上,A物体用线系在墙上,B 物体在力 F作用下向右运动,则B对A摩擦力做————功,A对B摩擦力做————功。
F
B
A
f1
f2
0
负
3.A、B两物体叠放在水平面上,A物体在力 F作用下在B物体上相对滑动,则B对A的摩擦力做————功,A对B做————功。
A
B
F
f1
f2
ΔS
S2
S1
W1= - fS1
W2= fS2
W1 + W2= f(S2 - S1 )= - f Δ S
负
正
作用力与反作用力做功没有必然关系
1、物理意义:是表示力对物体做功快慢的物理量。
3、公式:
比值定义法
4、功率是标量。
5、功率的单位:
瓦特(W)常用单位: kW
四、功率
2、定义:功W跟完成这些功所用时间t的比值
说明:即使是同一个力做功,做功的功率也可能是变化的,在一段时间内力对物体做功的功率,实际上是这段时间内力对物体做功的平均功率。
平均功率:描述一段时间内做功的平均快慢
瞬时功率:表示在某一时刻做功的快慢
P=
t
W
当 t 很短很短时,此式表示瞬时功率
当 t 表示一段时间时,此式表示平均功率
平均功率和瞬时功率
功率与速度的关系
P=Fv
W=Fscosα
P=
t
W
P=Fvcosα
若力与速度不再一条直线上呢?
功率与速度的关系
P=F v cosα
若v表示瞬时速度,则P 表示瞬时功率
若 v表示平均速度,则P 表示平均功率
对于公式 P = F v
1、当P 一定时,F 和 v 有什么关系?
2、当F 一定时,P 和 v 有什么关系?
3、当v 一定时,F 和 P 有什么关系?
当F与v同方向时(α=0),P=Fv
例题2
注意:汽车的功率就是汽车牵引力的功率
P=F v
发动机的实际功率
发动机的牵引力
机车的瞬时速度
类型1:机车以恒定功率 P 启动
机车启动问题
P=F v
发动机的实际功率
发动机的牵引力
机车的瞬时速度
当F=F阻时,
a=0 ,v达到最大
保持
vm
匀速
v
F=
v
P
a=
m
F-F阻
↑
→
↓
↑
→
→
↓
↓
vm=
F阻
P
加速度逐渐减小的变加速直线运动
匀速直线运动
vm
机车以恒定功率启动的v- t 图
机车启动问题
先做加速度逐渐减小的变加速直线运动,最终以速度 做匀速直线运动。
vm=
F阻
P
v
t
0
类型2:机车以恒定加速度 a 启动
当F= F阻时,
a=0 ,v达到最大
保持
vm
匀速
F=
v
P额
a=
m
F-F阻
↑
→
↓
v
↑
↓
→
→
↓
vm=
F阻
P额
加速度逐渐减小的变加速直线运动
匀速直线运动
a=
m
F-F阻
→
→
→
→
F
→
v
↑
P=F v
↑
↑
→
当P= P额时,保持P额继续加速
匀加速直线运动
机车以恒定加速度启动的v- t 图
先做匀加速直线运动,再做加速度逐渐减小的变加速直线运动,最终以速度 做匀速直线运动。
v
t
0
vm=
F阻
P额
vm
光滑水平面上的物块在弹簧弹力作用下从A点运动到B点,思考能否用W=Fl求弹簧弹力对物体所做的功?
思考:
A
B
对于变力做功不能直接套用公式
求解,但可依物理规律通过技巧的转化,将变力做功转化为恒力做功间接求解。
1.平均力法:
若变力大小随位移是线性变化,且方向不变时,可将变力的平均值求出后用公式
计算。如弹簧的弹力做功就可以用此法计算。
四、变力做功
2.利用F-x图像,F-x图线与坐标轴所包围的面
积即是力F做功的数值。
4.转换研究对象法(等效转换法)
5.用动能定理或能量守恒进行求解:
3. 无限分小法(微元法)来求, 过程无限分小后, 可认为每小段是恒力做功。
例1.一辆马车在力F的作用下绕半径为50 m的圆形轨道做匀速圆周运动,已知车子所受阻力为100N,当车运动一周回到原位置时,车子克服阻力所做的功为多少?
解:阻力的方向时刻在变,是变力做功的问题,不能直接由功的公式计算。
采用微元法解之,将圆分成很多很多小段,在这些小段中,力可以看作恒力,于是
Wf = – fΔs1 – fΔs2 – fΔs3 – fΔs4 – fΔs5 – ……
= – fs= – Fs = – 100×2πR= – 3.14 ×104 J
W克= – Wf= 3.14 ×104 J
解二:用图像法
因为阻力F=kx,以F为纵坐标,F方向上的位移x为横坐标,作出F-x图像,如图右下图,
X
F
0
x1
x2
kx1
kx2
曲线下面积的值等于F对铁钉做的功. (示功图)?
由于两次做功相等,故有:?
S1 = S2 (面积),即:
1/2× kx12=1/2× k(x2+x1)(x2-x1),
解后有:x2= x1=1.41 cm.
∴ △x=x2-x1=0.41 cm.
