7.2 万有引力定律(共28张PPT)
文档属性
| 名称 | 7.2 万有引力定律(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-26 00:00:00 | ||
图片预览



文档简介
(共28张PPT)
中物理
第七章 万有引力与宇宙航行
(高一 下)
第2节 万有引力定律
新教材人教版 物理(高中必修第二册)
思考:是什么力支配着行星绕着太阳做如此和谐而有规律的运动呢?
课堂引入
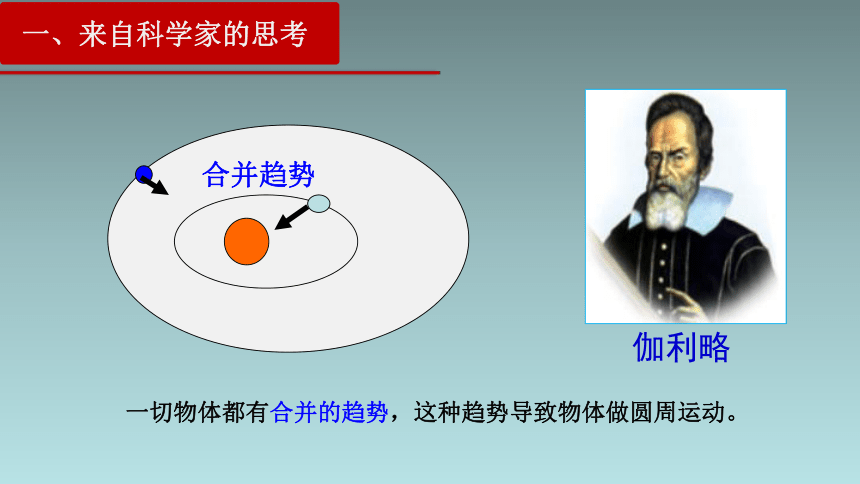
一、来自科学家的思考
合并趋势
伽利略
一切物体都有合并的趋势,这种趋势导致物体做圆周运动。
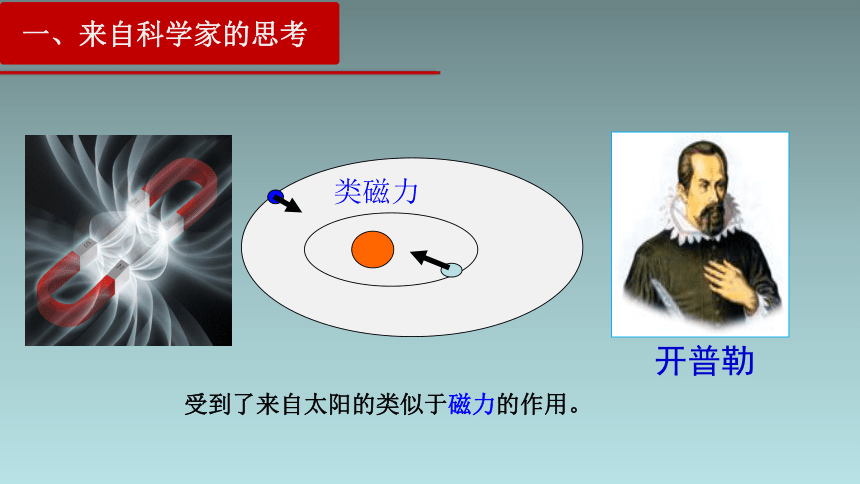
受到了来自太阳的类似于磁力的作用。
开普勒
类磁力
一、来自科学家的思考
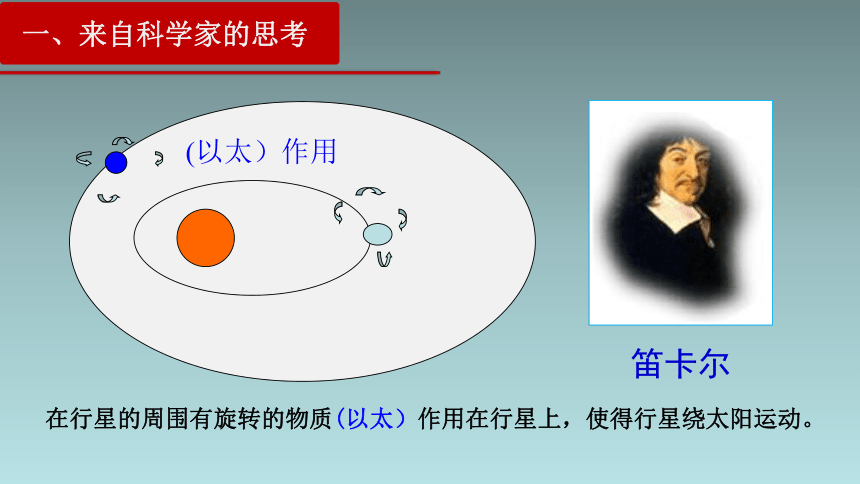
在行星的周围有旋转的物质(以太)作用在行星上,使得行星绕太阳运动。
(以太)作用
笛卡尔
一、来自科学家的思考
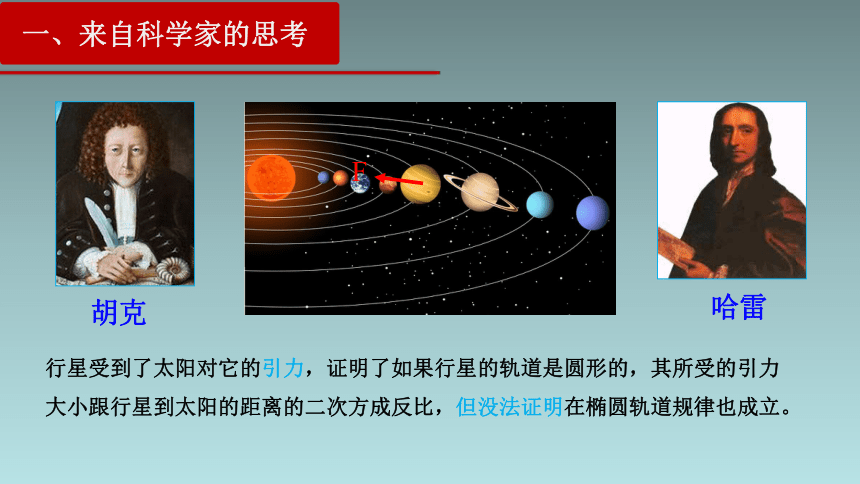
行星受到了太阳对它的引力,证明了如果行星的轨道是圆形的,其所受的引力大小跟行星到太阳的距离的二次方成反比,但没法证明在椭圆轨道规律也成立。
F
胡克
哈雷
一、来自科学家的思考
牛顿 (1643—1727)
牛顿在前人对惯性研究的基础上,开始思考“物体怎样才会不沿直线运动”,他的回答是:以任何方式改变速度,都需要力。行星做匀速圆周运动需要指向圆心的力,这个力应该就是太阳对它的引力。
一、来自科学家的思考
二、行星与太阳间的引力
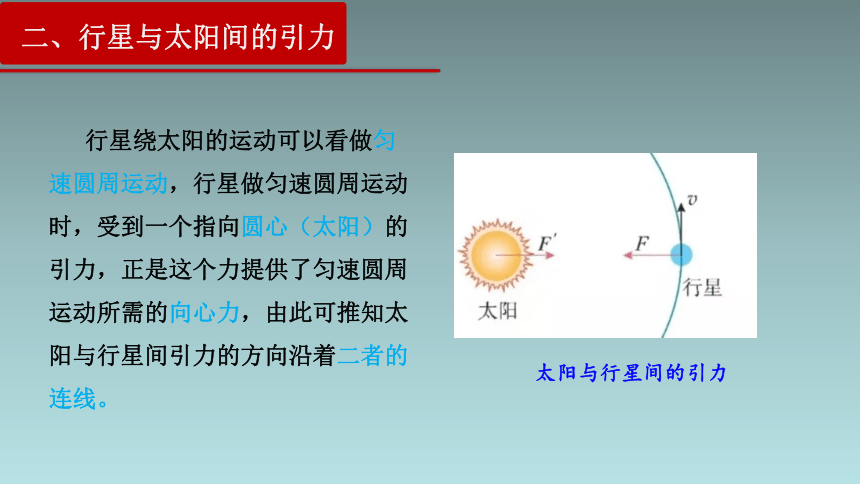
行星绕太阳的运动可以看做匀速圆周运动,行星做匀速圆周运动时,受到一个指向圆心(太阳)的引力,正是这个力提供了匀速圆周运动所需的向心力,由此可推知太阳与行星间引力的方向沿着二者的连线。
太阳与行星间的引力
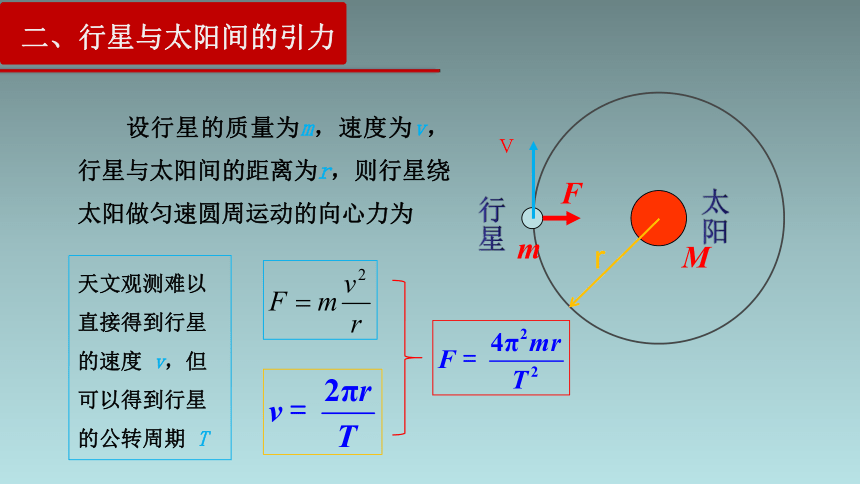
设行星的质量为m,速度为v,行星与太阳间的距离为r,则行星绕太阳做匀速圆周运动的向心力为
天文观测难以直接得到行星的速度 v,但可以得到行星的公转周期 T
F
行星
太阳
M
m
V
二、行星与太阳间的引力
r
根据开普勒第三定律
所以
太阳对行星的引力
即太阳对不同行星的引力,与行星的质量m成正比,与r2成反比。
F
行星
太阳
M
m
V
二、行星与太阳间的引力
r
类比法
牛 三
F 和F ′是一对作用力和反作用力,那么可以得出F大小跟太阳质量M、行星质量m的关系式有什么关系?
G为比例系数,与太阳、行星无关。
方向:沿着太阳与行星间的连线
F
F
M
m
V
二、行星与太阳间的引力
三、月—地检验
猜想:地球对月球的引力,与地球对树上苹果的吸引力是同一种性质的力吗?
1.牛顿的思考:
地球对月球的引力、地球对地面上物体的引力若为同一种力,其大小的表达式满足
三、月—地检验
三、月—地检验
R
r
F
结论:地面物体受地球的引力、月球所受地球的引力,与太阳、行星间的引力,遵循相同的规律。
三、月—地检验
四、万有引力定律
2.表达式:
3.适用条件:
(1)两质点间(两物体间距远大于物体的线度)
(2)两均质球体间(r 为两球球心间的距离)
1.内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量m1和m2的乘积成正比、与它们之间距离r 的二次方成反比。
4.对万有引力定律的理解:
(1)普遍性:它存在于宇宙中任何客观存在的两个物体之间。
(2)相互性:任何两物体间的相互引力,都是一对作用力和反作用力,符合牛顿第三定律。
(3)宏观性:通常情况下,万有引力非常小,只有在质量巨大的天体间或天体与天体附近的物体间,它的作用才有实际的物理意义。
(4)独立性:万有引力的大小只与它们的质量和距离有关,与其他的因素均无关。不管它们之间是否还有其他作用力。
四、万有引力定律
5.发现万有引力定律的重要意义:
揭示了地面上物体运动的规律和天体上物体的运动遵从同一规律,让人们认识到天体上物体的运动规律也是可以认识的,解放了人们的思想,给人们探索自然的奥秘建立了极大信心, 对后来的物理学、天文学的发展具有深远的影响。
四、万有引力定律
五、引力常量
1686年牛顿发现万有引力定律后,却无法算出两个天体间的引力大小。
100多年以后,英国物理学家卡文迪什利用扭秤装置,第一次比较准确地测出了引力常量。
五、引力常量
1.扭秤装置把微小力通过杠杆旋转明显反映出来(一次放大);
2.扭转角度(微小形变)通过光标的移动来反映(二次放大),从而确定物体间的万有引力。
装置的巧妙之处:两次放大及等效的思想 。
3.标准值:G=6.67259×10-11N·m2/kg2,
通常取G=6.67×10-11N·m2/kg2 。
测定引力常量的重要意义
1.证明了万有引力的存在;
2.“开创了测量弱力的新时代” (英国物理学家玻印廷语);
3.使得万有引力定律有了真正的实用价值,可测定远离地球的一些天体的质量、平均密度等。
五、引力常量
G=6.67×10-11N·m2/kg2
课堂小结
【典例1】(2021·全国高一单元测试)量纲分析是物理学中的一种很重要的研究方法。例如,任何两个物体之间都存在相互作用的引力,引力的大小与这两个物体的质量的乘积成正比,与这两个物体之间的距离的平方成反比,其表达式可写为,式中G为万有引力常量,你可能不知道G的具体单位,但是你可以结合单位换算(量纲分析)对其做出推断,则根据你的推断,下列关于G的具体单位,表述正确的是( )
A.N·m/kg B. C. D.
典例分析
【正确答案】B
【典例2】(2021·全国高一专题练习)(多选)关于太阳与行星间的引力,下列说法中正确的是( )
A.由于地球比木星离太阳近,所以太阳对地球的引力一定比对木星的引力大
B.行星绕太阳沿椭圆轨道运动时,在从近日点向远日点运动时所受引力变小
C.由F= 可知G= ,由此可见G与F和r2的乘积成正比,与M太和m的乘积成反比
D.行星绕太阳运动的椭圆轨道可近似看成圆轨道,行星做圆周运动的向心力来源于太阳对行星的引力
典例分析
【正确答案】BD
【典例3】(2020·辽宁高一期末)“月地检验”是牛顿为了证明以下猜想:“使月球绕地球运动的力”与“使苹果落地的力”遵循同样的规律。牛顿当年知道月地之间距离3.84×108米,地球半径6.4×106米,那么他需要验证( )
A.地球吸引苹果的力约为地球吸引月球的力的
B.自由落体在月球表面的加速度约为地球表面的
C.苹果在月球表面受到的引力约为在地球表面的
D.月球公转的加速度约为苹果落向地面加速度的
典例分析
【正确答案】D
【典例4】(2020·北京市第四十三中学高一月考)“北斗卫星导航系统”是中国自行研制的全球卫星导航系统,同步卫星是其重要组成部分。如图所示,发射同步卫星时,可以先将卫星发射至近地圆轨道1,然后经过一系列的变轨过程,将卫星送入同步圆轨道2,A点在轨道1上,B、C两点在轨道2上。卫星在轨道1、轨道2上的运动均可视为匀速圆周运动。在该卫星远离地球的过程中,地球对卫星的引力( )
A.越来越大 B.越来越小
C.保持不变 D.先变大后变小
典例分析
【正确答案】B
【典例5】(2021·山西吕梁市·高三一模)2020年12月1日嫦娥五号探测器实施月面“挖土”成功,“挖土”采用了钻取和表取两种模式。假设月球可看作质量分布均匀的球体,其质量为M,半径为R。已知质量分布均匀的球壳对壳内物体的万有引力为零,万有引力常量为G。某次钻取中质量为m的钻尖进入月球表面以下h深处,则此时月球对钻尖的万有引力为( )
A.0 B. C. D.
典例分析
【正确答案】D
【解析】月球质量与剩余质量关系为
设月球密度为 ,月球对钻尖的万有引力为
故选D。
典例分析
中物理
第七章 万有引力与宇宙航行
(高一 下)
第2节 万有引力定律
新教材人教版 物理(高中必修第二册)
思考:是什么力支配着行星绕着太阳做如此和谐而有规律的运动呢?
课堂引入
一、来自科学家的思考
合并趋势
伽利略
一切物体都有合并的趋势,这种趋势导致物体做圆周运动。
受到了来自太阳的类似于磁力的作用。
开普勒
类磁力
一、来自科学家的思考
在行星的周围有旋转的物质(以太)作用在行星上,使得行星绕太阳运动。
(以太)作用
笛卡尔
一、来自科学家的思考
行星受到了太阳对它的引力,证明了如果行星的轨道是圆形的,其所受的引力大小跟行星到太阳的距离的二次方成反比,但没法证明在椭圆轨道规律也成立。
F
胡克
哈雷
一、来自科学家的思考
牛顿 (1643—1727)
牛顿在前人对惯性研究的基础上,开始思考“物体怎样才会不沿直线运动”,他的回答是:以任何方式改变速度,都需要力。行星做匀速圆周运动需要指向圆心的力,这个力应该就是太阳对它的引力。
一、来自科学家的思考
二、行星与太阳间的引力
行星绕太阳的运动可以看做匀速圆周运动,行星做匀速圆周运动时,受到一个指向圆心(太阳)的引力,正是这个力提供了匀速圆周运动所需的向心力,由此可推知太阳与行星间引力的方向沿着二者的连线。
太阳与行星间的引力
设行星的质量为m,速度为v,行星与太阳间的距离为r,则行星绕太阳做匀速圆周运动的向心力为
天文观测难以直接得到行星的速度 v,但可以得到行星的公转周期 T
F
行星
太阳
M
m
V
二、行星与太阳间的引力
r
根据开普勒第三定律
所以
太阳对行星的引力
即太阳对不同行星的引力,与行星的质量m成正比,与r2成反比。
F
行星
太阳
M
m
V
二、行星与太阳间的引力
r
类比法
牛 三
F 和F ′是一对作用力和反作用力,那么可以得出F大小跟太阳质量M、行星质量m的关系式有什么关系?
G为比例系数,与太阳、行星无关。
方向:沿着太阳与行星间的连线
F
F
M
m
V
二、行星与太阳间的引力
三、月—地检验
猜想:地球对月球的引力,与地球对树上苹果的吸引力是同一种性质的力吗?
1.牛顿的思考:
地球对月球的引力、地球对地面上物体的引力若为同一种力,其大小的表达式满足
三、月—地检验
三、月—地检验
R
r
F
结论:地面物体受地球的引力、月球所受地球的引力,与太阳、行星间的引力,遵循相同的规律。
三、月—地检验
四、万有引力定律
2.表达式:
3.适用条件:
(1)两质点间(两物体间距远大于物体的线度)
(2)两均质球体间(r 为两球球心间的距离)
1.内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量m1和m2的乘积成正比、与它们之间距离r 的二次方成反比。
4.对万有引力定律的理解:
(1)普遍性:它存在于宇宙中任何客观存在的两个物体之间。
(2)相互性:任何两物体间的相互引力,都是一对作用力和反作用力,符合牛顿第三定律。
(3)宏观性:通常情况下,万有引力非常小,只有在质量巨大的天体间或天体与天体附近的物体间,它的作用才有实际的物理意义。
(4)独立性:万有引力的大小只与它们的质量和距离有关,与其他的因素均无关。不管它们之间是否还有其他作用力。
四、万有引力定律
5.发现万有引力定律的重要意义:
揭示了地面上物体运动的规律和天体上物体的运动遵从同一规律,让人们认识到天体上物体的运动规律也是可以认识的,解放了人们的思想,给人们探索自然的奥秘建立了极大信心, 对后来的物理学、天文学的发展具有深远的影响。
四、万有引力定律
五、引力常量
1686年牛顿发现万有引力定律后,却无法算出两个天体间的引力大小。
100多年以后,英国物理学家卡文迪什利用扭秤装置,第一次比较准确地测出了引力常量。
五、引力常量
1.扭秤装置把微小力通过杠杆旋转明显反映出来(一次放大);
2.扭转角度(微小形变)通过光标的移动来反映(二次放大),从而确定物体间的万有引力。
装置的巧妙之处:两次放大及等效的思想 。
3.标准值:G=6.67259×10-11N·m2/kg2,
通常取G=6.67×10-11N·m2/kg2 。
测定引力常量的重要意义
1.证明了万有引力的存在;
2.“开创了测量弱力的新时代” (英国物理学家玻印廷语);
3.使得万有引力定律有了真正的实用价值,可测定远离地球的一些天体的质量、平均密度等。
五、引力常量
G=6.67×10-11N·m2/kg2
课堂小结
【典例1】(2021·全国高一单元测试)量纲分析是物理学中的一种很重要的研究方法。例如,任何两个物体之间都存在相互作用的引力,引力的大小与这两个物体的质量的乘积成正比,与这两个物体之间的距离的平方成反比,其表达式可写为,式中G为万有引力常量,你可能不知道G的具体单位,但是你可以结合单位换算(量纲分析)对其做出推断,则根据你的推断,下列关于G的具体单位,表述正确的是( )
A.N·m/kg B. C. D.
典例分析
【正确答案】B
【典例2】(2021·全国高一专题练习)(多选)关于太阳与行星间的引力,下列说法中正确的是( )
A.由于地球比木星离太阳近,所以太阳对地球的引力一定比对木星的引力大
B.行星绕太阳沿椭圆轨道运动时,在从近日点向远日点运动时所受引力变小
C.由F= 可知G= ,由此可见G与F和r2的乘积成正比,与M太和m的乘积成反比
D.行星绕太阳运动的椭圆轨道可近似看成圆轨道,行星做圆周运动的向心力来源于太阳对行星的引力
典例分析
【正确答案】BD
【典例3】(2020·辽宁高一期末)“月地检验”是牛顿为了证明以下猜想:“使月球绕地球运动的力”与“使苹果落地的力”遵循同样的规律。牛顿当年知道月地之间距离3.84×108米,地球半径6.4×106米,那么他需要验证( )
A.地球吸引苹果的力约为地球吸引月球的力的
B.自由落体在月球表面的加速度约为地球表面的
C.苹果在月球表面受到的引力约为在地球表面的
D.月球公转的加速度约为苹果落向地面加速度的
典例分析
【正确答案】D
【典例4】(2020·北京市第四十三中学高一月考)“北斗卫星导航系统”是中国自行研制的全球卫星导航系统,同步卫星是其重要组成部分。如图所示,发射同步卫星时,可以先将卫星发射至近地圆轨道1,然后经过一系列的变轨过程,将卫星送入同步圆轨道2,A点在轨道1上,B、C两点在轨道2上。卫星在轨道1、轨道2上的运动均可视为匀速圆周运动。在该卫星远离地球的过程中,地球对卫星的引力( )
A.越来越大 B.越来越小
C.保持不变 D.先变大后变小
典例分析
【正确答案】B
【典例5】(2021·山西吕梁市·高三一模)2020年12月1日嫦娥五号探测器实施月面“挖土”成功,“挖土”采用了钻取和表取两种模式。假设月球可看作质量分布均匀的球体,其质量为M,半径为R。已知质量分布均匀的球壳对壳内物体的万有引力为零,万有引力常量为G。某次钻取中质量为m的钻尖进入月球表面以下h深处,则此时月球对钻尖的万有引力为( )
A.0 B. C. D.
典例分析
【正确答案】D
【解析】月球质量与剩余质量关系为
设月球密度为 ,月球对钻尖的万有引力为
故选D。
典例分析
