人教版数学八年级下册同步课件:18.2.3 正方形(共30张PPT)
文档属性
| 名称 | 人教版数学八年级下册同步课件:18.2.3 正方形(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 932.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 15:52:18 | ||
图片预览


文档简介
(共30张PPT)
第十八章 平行四边形
18.2.3 正方形
知识回顾
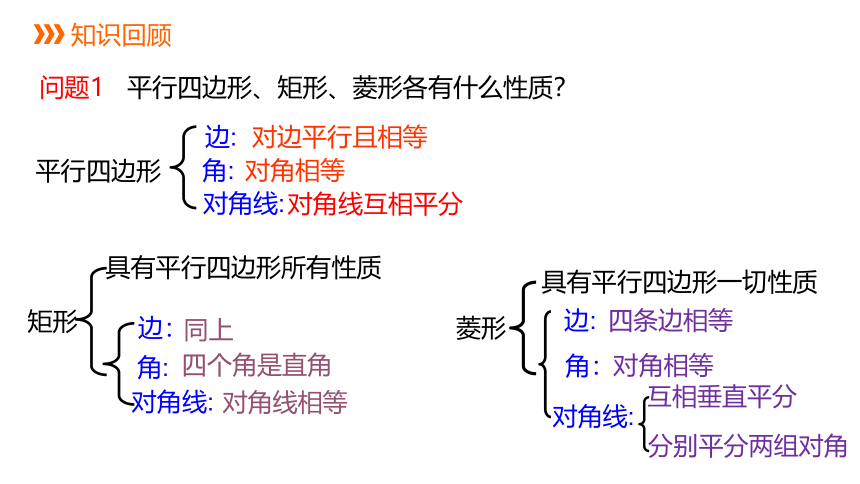
问题1 平行四边形、矩形、菱形各有什么性质?
平行四边形
边:
角:
对角线:
对边平行且相等
对角相等
对角线互相平分
矩形
角:
四个角是直角
对角线:
对角线相等
边:
同上
具有平行四边形所有性质
菱形
边:
四条边相等
对角线:
互相垂直平分
分别平分两组对角
对角相等
具有平行四边形一切性质
角:
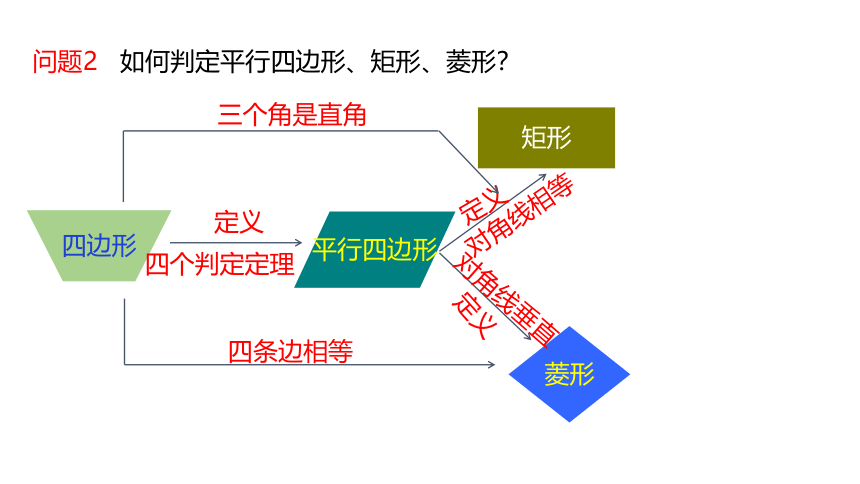
问题2 如何判定平行四边形、矩形、菱形?
平行四边形
矩形
菱形
四边形
三个角是直角
四条边相等
定义
四个判定定理
定义
对角线相等
定义
对角线垂直
情景导入
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
你还能举出其他的例子吗?
获取新知
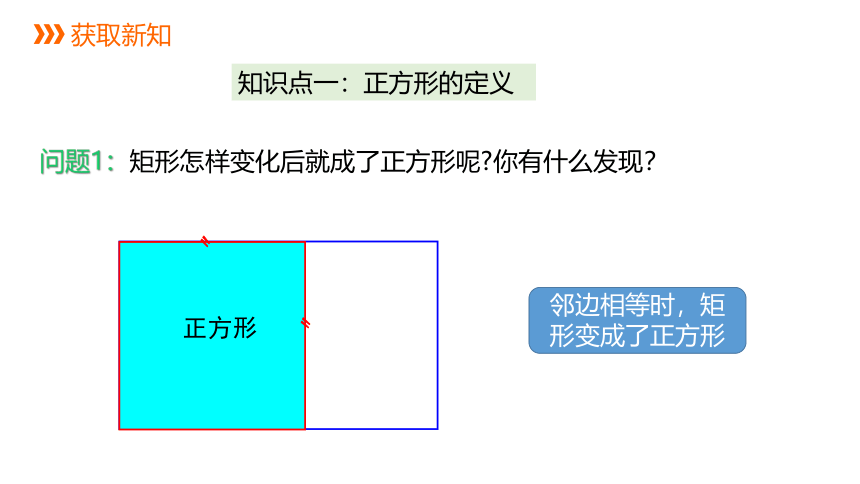
知识点一:正方形的定义
矩 形
〃
〃
问题1:矩形怎样变化后就成了正方形呢 你有什么发现?
正方形
邻边相等时,矩形变成了正方形
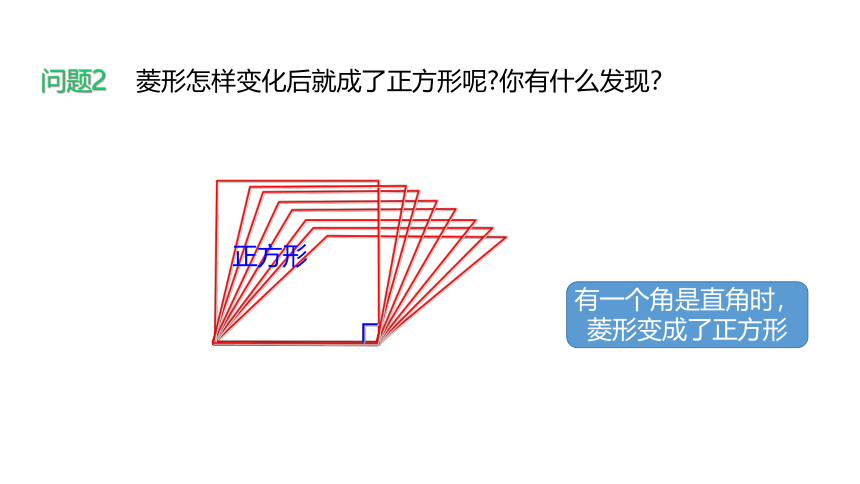
问题2 菱形怎样变化后就成了正方形呢 你有什么发现?
正方形
有一个角是直角时,菱形变成了正方形
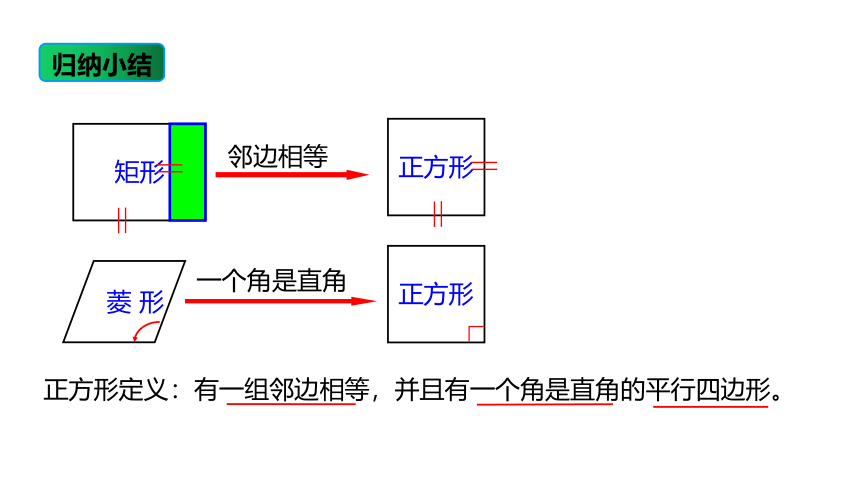
邻边相等
矩形
正方形
菱 形
一个角是直角
正方形
∟
正方形定义:有一组邻边相等,并且有一个角是直角的平行四边形。
归纳小结
获取新知
知识点二:正方形的性质
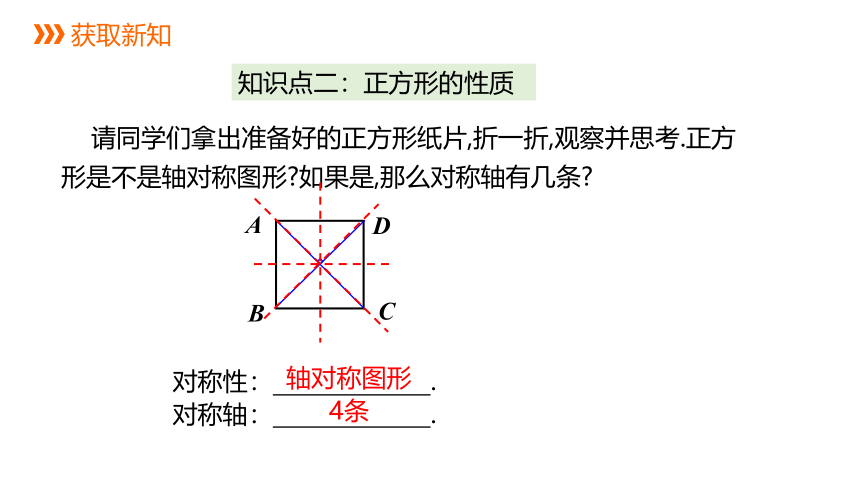
请同学们拿出准备好的正方形纸片,折一折,观察并思考.正方形是不是轴对称图形 如果是,那么对称轴有几条
对称性: .
对称轴: .
轴对称图形
4条
A
B
C
D
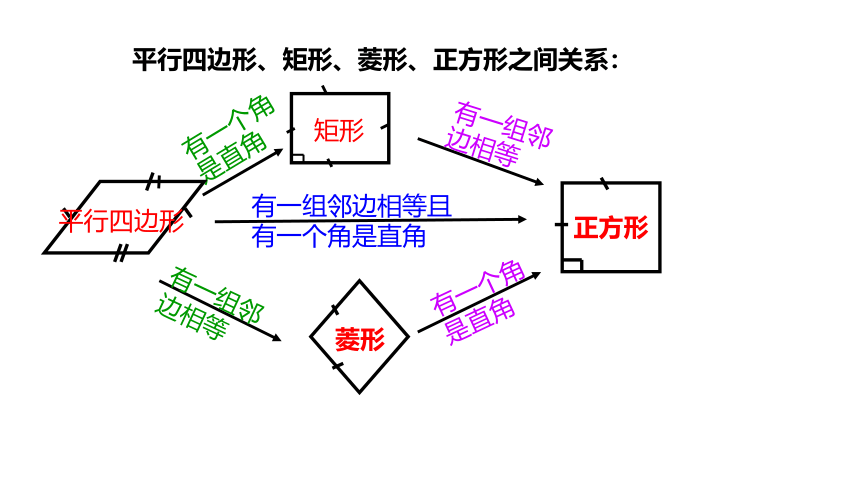
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
平行四边形
平行四边形、矩形、菱形、正方形之间关系:
矩形
菱形
正方形
矩形
菱形
正
方
形
平行四边形
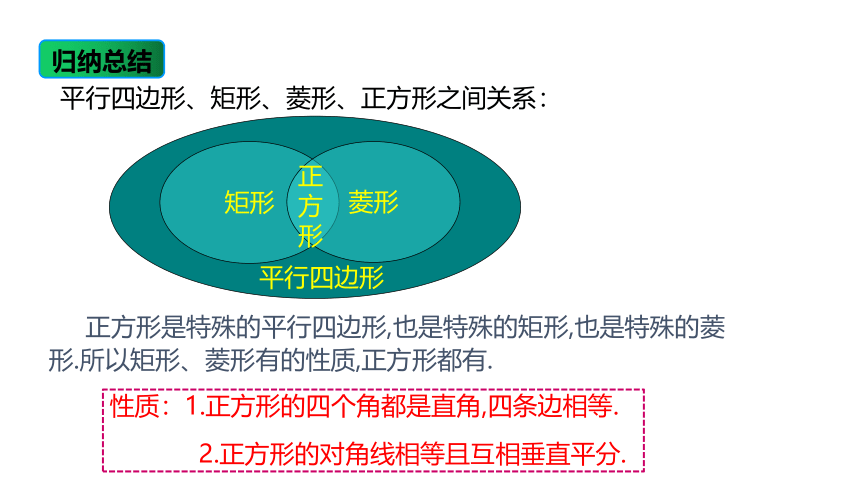
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
平行四边形、矩形、菱形、正方形之间关系:
性质:1.正方形的四个角都是直角,四条边相等.
2.正方形的对角线相等且互相垂直平分.
归纳总结
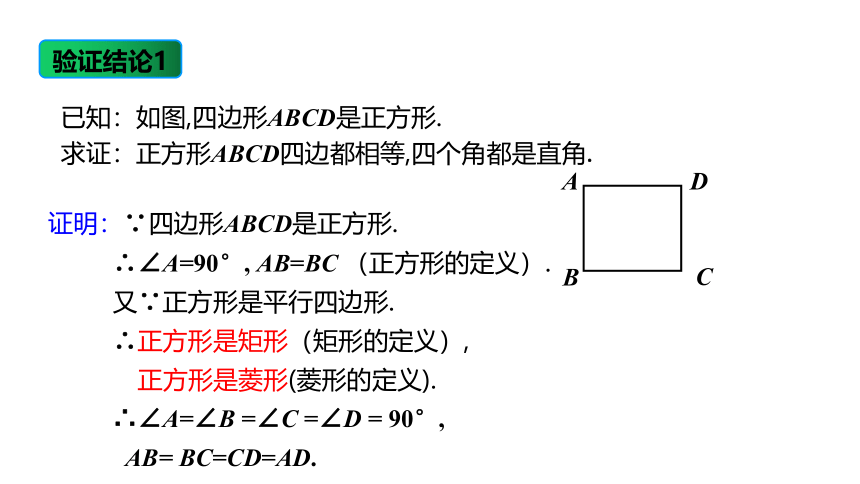
已知:如图,四边形ABCD是正方形.
求证:正方形ABCD四边都相等,四个角都是直角.
A
B
C
D
证明:∵四边形ABCD是正方形.
∴∠A=90°, AB=BC (正方形的定义).
又∵正方形是平行四边形.
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义).
∴∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.
验证结论1
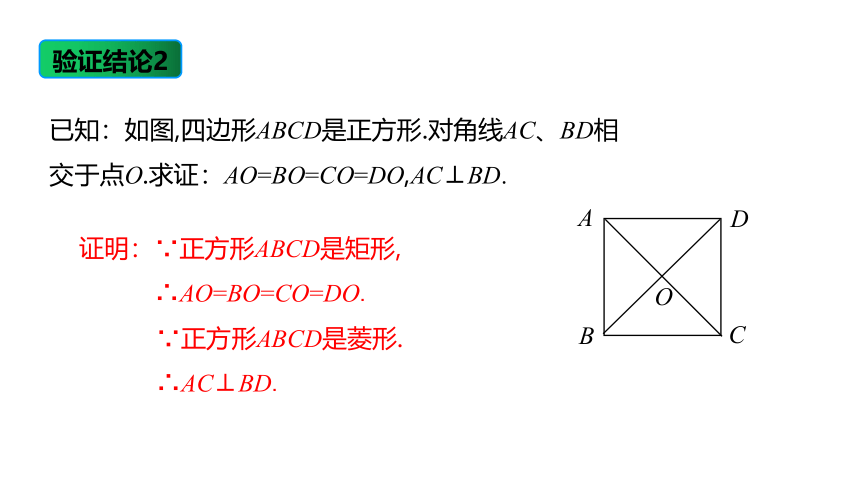
已知:如图,四边形ABCD是正方形.对角线AC、BD相交于点O.求证:AO=BO=CO=DO,AC⊥BD.
A
B
C
D
O
证明:∵正方形ABCD是矩形,
∴AO=BO=CO=DO.
∵正方形ABCD是菱形.
∴AC⊥BD.
验证结论2
例题讲解
例1 求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
已知: 如图,四边形ABCD是正方形,对角线AC、BD相
交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
A
D
C
B
O
A
D
C
B
O
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都
是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO.
例2 如图,在正方形ABCD中, ΔBEC是等边三角形,
求证: ∠EAD=∠EDA=15° .
证明:∵ ΔBEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°,
∵ 四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴AB=BE=CE=CD, ∠ABE= ∠DCE=30°,
∴△ABE,△DCE是等腰三角形,
∴∠BAE= ∠BEA= ∠CDE= ∠CED=75°,
∴∠EAD= ∠EDA=90°-75°=15°.
巩固练习
已知:如图,在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°.
证明:∵CE⊥AF, ∴∠ADC=∠AEM=90°.
又∵∠CMD=∠AME,
∴∠1=∠2.
又∵CD=AD,∠ADF=∠MDC,
∴Rt△CDM≌Rt△ADF(ASA).
∴DM=DF.
∴∠DMF=∠DFM.
∵∠ADF=90°,∴∠MFD=45°.
获取新知
活动1 把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.量量看是不是正方形.
正方形
菱形
猜想 满足怎样条件的菱形是正方形?
正方形
一个角是直角
对角线相等
知识点三:正方形的判定
已知:如图,在菱形ABCD中,AC , DB是它的两条对角线,
AC=DB.
求证:四边形ABCD是正方形.
验证猜想
A
B
C
D
O
对角线相等的菱形是正方形.
证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥DB.
∵AC=DB,
∴ AO=BO=CO=DO,
∴△AOD,△AOB,△COD,△BOC是等腰直角三角形,
∴∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴四边形ABCD是正方形.
A
B
C
D
O
活动2 准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形,可量一量验证验证.
正方形
猜想 满足怎样条件的矩形是正方形?
矩形
正方形
一组邻边相等
对角线互相垂直
已知:如图,在矩形ABCD中,AC , DB是它的两条对角线,
AC⊥DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴ AO=CO=BO=DO ,∠ADC=90°.
∵AC⊥DB,
∴ AD=AB=BC=CD,
∴四边形ABCD是正方形.
A
B
C
D
O
对角线互相垂直的矩形是正方形.
验证猜想
正方形判定的几条途径:
正方形
正方形
+
+
先判定菱形
先判定矩形
矩形条件(二选一)
菱形条件(二选一)
一个直角,
一组邻边相等,
总结归纳
对角线相等
对角线垂直
平行四边形
正方形
一组邻边相等
一内角是直角
例题讲解
例3 已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.
求证:四边形CFDE是正方形.
∵∠C=90°, DE⊥BC于E,DF⊥AC于F,
∴∠DEC=90°, ∠DFC=90°,
∴四边形CFDE有三个直角, 它是矩形.
又∵CD平分∠ACB,
∴ DE=DF.
∴四边形CFDE是正方形.
证明:
随堂演练
1.正方形具有而矩形不一定具有的性质是 ( )
A.四个角相等
B.对角线互相垂直平分
C.对角互补
D.对角线相等
B
2. 平行四边形、矩形、菱形、正方形共有的性质是( )
A.对角线相等
B.对角线互相平分
C.对角线互相垂直
D.对角线互相垂直平分
B
3.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是( )
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
C
A
B
C
D
O
4. 如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.
求证:△APB≌△DPC;
解:∵四边形ABCD是正方形,
∴∠ABC=∠DCB=90°.
∵PB=PC,
∴∠PBC=∠PCB.
∴∠ABC-∠PBC=∠DCB-∠PCB,
即∠ABP=∠DCP.
又∵AB=DC,PB=PC,
∴△APB≌△DPC.
证明:过点D作DG⊥AB,垂足为G.
∵ DE⊥AC,DF⊥AB ,
∴∠DEC= ∠DFC=90°.
又∵ ∠C=90 °,
∴四边形ADFC是矩形.
∵AD是∠CAB的平分线,DE⊥AC,DG⊥AB,
∴ DE=DG.
同理得DG=DF,
∴ED=DF,
∴四边形ADFC是正方形.
5.如图,在直角三角形中,∠C=90°,∠A、∠B的平分线交于点D.DE⊥AC,DF⊥AB.求证:四边形CEDF为正方形.
A
B
C
D
E
F
G
课堂小结
1.正方形的性质
四条边都相等
两组对边分别平行
两条对角线互相平分
边
对角线
角
两组对角分别相等
四个角都是直角
两条对角线互相垂直,每一条对角线平分一组对角
两条对角线相等
正方形
5种识别方法
三个角是直角
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
四边形
平行四边形
矩形
菱形
正方形
2.正方形的判定
四条边都相等
第十八章 平行四边形
18.2.3 正方形
知识回顾
问题1 平行四边形、矩形、菱形各有什么性质?
平行四边形
边:
角:
对角线:
对边平行且相等
对角相等
对角线互相平分
矩形
角:
四个角是直角
对角线:
对角线相等
边:
同上
具有平行四边形所有性质
菱形
边:
四条边相等
对角线:
互相垂直平分
分别平分两组对角
对角相等
具有平行四边形一切性质
角:
问题2 如何判定平行四边形、矩形、菱形?
平行四边形
矩形
菱形
四边形
三个角是直角
四条边相等
定义
四个判定定理
定义
对角线相等
定义
对角线垂直
情景导入
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
你还能举出其他的例子吗?
获取新知
知识点一:正方形的定义
矩 形
〃
〃
问题1:矩形怎样变化后就成了正方形呢 你有什么发现?
正方形
邻边相等时,矩形变成了正方形
问题2 菱形怎样变化后就成了正方形呢 你有什么发现?
正方形
有一个角是直角时,菱形变成了正方形
邻边相等
矩形
正方形
菱 形
一个角是直角
正方形
∟
正方形定义:有一组邻边相等,并且有一个角是直角的平行四边形。
归纳小结
获取新知
知识点二:正方形的性质
请同学们拿出准备好的正方形纸片,折一折,观察并思考.正方形是不是轴对称图形 如果是,那么对称轴有几条
对称性: .
对称轴: .
轴对称图形
4条
A
B
C
D
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
有一组邻边相等且有一个角是直角
平行四边形
平行四边形、矩形、菱形、正方形之间关系:
矩形
菱形
正方形
矩形
菱形
正
方
形
平行四边形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
平行四边形、矩形、菱形、正方形之间关系:
性质:1.正方形的四个角都是直角,四条边相等.
2.正方形的对角线相等且互相垂直平分.
归纳总结
已知:如图,四边形ABCD是正方形.
求证:正方形ABCD四边都相等,四个角都是直角.
A
B
C
D
证明:∵四边形ABCD是正方形.
∴∠A=90°, AB=BC (正方形的定义).
又∵正方形是平行四边形.
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义).
∴∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.
验证结论1
已知:如图,四边形ABCD是正方形.对角线AC、BD相交于点O.求证:AO=BO=CO=DO,AC⊥BD.
A
B
C
D
O
证明:∵正方形ABCD是矩形,
∴AO=BO=CO=DO.
∵正方形ABCD是菱形.
∴AC⊥BD.
验证结论2
例题讲解
例1 求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
已知: 如图,四边形ABCD是正方形,对角线AC、BD相
交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
A
D
C
B
O
A
D
C
B
O
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都
是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO.
例2 如图,在正方形ABCD中, ΔBEC是等边三角形,
求证: ∠EAD=∠EDA=15° .
证明:∵ ΔBEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°,
∵ 四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴AB=BE=CE=CD, ∠ABE= ∠DCE=30°,
∴△ABE,△DCE是等腰三角形,
∴∠BAE= ∠BEA= ∠CDE= ∠CED=75°,
∴∠EAD= ∠EDA=90°-75°=15°.
巩固练习
已知:如图,在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°.
证明:∵CE⊥AF, ∴∠ADC=∠AEM=90°.
又∵∠CMD=∠AME,
∴∠1=∠2.
又∵CD=AD,∠ADF=∠MDC,
∴Rt△CDM≌Rt△ADF(ASA).
∴DM=DF.
∴∠DMF=∠DFM.
∵∠ADF=90°,∴∠MFD=45°.
获取新知
活动1 把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.量量看是不是正方形.
正方形
菱形
猜想 满足怎样条件的菱形是正方形?
正方形
一个角是直角
对角线相等
知识点三:正方形的判定
已知:如图,在菱形ABCD中,AC , DB是它的两条对角线,
AC=DB.
求证:四边形ABCD是正方形.
验证猜想
A
B
C
D
O
对角线相等的菱形是正方形.
证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥DB.
∵AC=DB,
∴ AO=BO=CO=DO,
∴△AOD,△AOB,△COD,△BOC是等腰直角三角形,
∴∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴四边形ABCD是正方形.
A
B
C
D
O
活动2 准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形,可量一量验证验证.
正方形
猜想 满足怎样条件的矩形是正方形?
矩形
正方形
一组邻边相等
对角线互相垂直
已知:如图,在矩形ABCD中,AC , DB是它的两条对角线,
AC⊥DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴ AO=CO=BO=DO ,∠ADC=90°.
∵AC⊥DB,
∴ AD=AB=BC=CD,
∴四边形ABCD是正方形.
A
B
C
D
O
对角线互相垂直的矩形是正方形.
验证猜想
正方形判定的几条途径:
正方形
正方形
+
+
先判定菱形
先判定矩形
矩形条件(二选一)
菱形条件(二选一)
一个直角,
一组邻边相等,
总结归纳
对角线相等
对角线垂直
平行四边形
正方形
一组邻边相等
一内角是直角
例题讲解
例3 已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.
求证:四边形CFDE是正方形.
∵∠C=90°, DE⊥BC于E,DF⊥AC于F,
∴∠DEC=90°, ∠DFC=90°,
∴四边形CFDE有三个直角, 它是矩形.
又∵CD平分∠ACB,
∴ DE=DF.
∴四边形CFDE是正方形.
证明:
随堂演练
1.正方形具有而矩形不一定具有的性质是 ( )
A.四个角相等
B.对角线互相垂直平分
C.对角互补
D.对角线相等
B
2. 平行四边形、矩形、菱形、正方形共有的性质是( )
A.对角线相等
B.对角线互相平分
C.对角线互相垂直
D.对角线互相垂直平分
B
3.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是( )
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
C
A
B
C
D
O
4. 如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.
求证:△APB≌△DPC;
解:∵四边形ABCD是正方形,
∴∠ABC=∠DCB=90°.
∵PB=PC,
∴∠PBC=∠PCB.
∴∠ABC-∠PBC=∠DCB-∠PCB,
即∠ABP=∠DCP.
又∵AB=DC,PB=PC,
∴△APB≌△DPC.
证明:过点D作DG⊥AB,垂足为G.
∵ DE⊥AC,DF⊥AB ,
∴∠DEC= ∠DFC=90°.
又∵ ∠C=90 °,
∴四边形ADFC是矩形.
∵AD是∠CAB的平分线,DE⊥AC,DG⊥AB,
∴ DE=DG.
同理得DG=DF,
∴ED=DF,
∴四边形ADFC是正方形.
5.如图,在直角三角形中,∠C=90°,∠A、∠B的平分线交于点D.DE⊥AC,DF⊥AB.求证:四边形CEDF为正方形.
A
B
C
D
E
F
G
课堂小结
1.正方形的性质
四条边都相等
两组对边分别平行
两条对角线互相平分
边
对角线
角
两组对角分别相等
四个角都是直角
两条对角线互相垂直,每一条对角线平分一组对角
两条对角线相等
正方形
5种识别方法
三个角是直角
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
四边形
平行四边形
矩形
菱形
正方形
2.正方形的判定
四条边都相等
