第三章平行四边形全章学案

3.1.1平行四边形的性质（一）
学习目标：
学习四边形的概念、结构、分类；
记忆平行四边形的概念、结构、表示方法、读法；
记忆平行四边形的性质；
会画平行四边形的图形
重点：平行四边形性质的应用
预习导学——不看不讲
学一学：阅读教材P67~P68内容，解答下列问题：
我能说出日常生活中这些物体的形状是四边形 ：
四边形有 这些特征。
这样的图形叫做四边形； 叫做四边形的边，
叫做四边形的顶点，
叫做四边形的对角线， 叫做四边形的内角，简称四边形的 ， 叫做四边形的对角，相对的两条边叫做四边形的 。
我能说出下图中四边形的所有结构。
这个四边形可以记作 ，
有这四个角分别是 ， ， ， ，
对角线是 和
边AB的对边是 ；边AD的对边是 ；
5、四边形可以分为两类： 和 ；
6、下列四边形哪些是凸四边形？哪些是凹四边形？
说一说：
1、 叫做平行四边形；
2、如图，在四边形ABCD中
则四边形ABCD是平行四边形，记作 ，读作
3、由平行四边形的定义可以看出要判定一个四边形是否是平行四边形只要 个条件，它们分别是： 。
学一学：
我也能画一个平行四边形：
议一议：阅读P69~P71页的内容，解答下列问题：
量一量我刚才画的平行四边形可以猜测出平行四边形的对边 ，平行四边形的对角 ；
我还可以证明我的猜测：
在 ABCD中，作对角线AC。
由于AB// ，因此（两直线平行， ）。
同理，由于BC// ，因此（两直线平行， ）
从而 （ ）
即
我还可以通过证明与全等后说明
请根据图形同组之间相互口述说明与全等的证明过程。
【归纳总结】
平行四边形的性质有： ，
。
结合图形用几何语言可以表述为：
在 EFGH中，EF// ，FG// ；
EH= ， =HG；
【课堂展示】
一块平行四边形的木板，其中木板的一边长为45cm，
相邻的另一边长为55cm，试求这块木板的周长。
在上块木板中，若
3、夹在两条平行线间的平行线段 。如图，直线，
AB、CD是 与 之间的任意两条平行线段，则AB CD
【当堂检测】（每小题25分，共100分）
我今天的收获：
3.1.1平行四边形的性质（二）
学习目标：
学习平行四边形关于对角线的性质；
学习中心对称图形的概念
重点：
平行四边形关于对角线性质的推导；
平行四边形对角线性质的应用。
预习导学——不看不讲
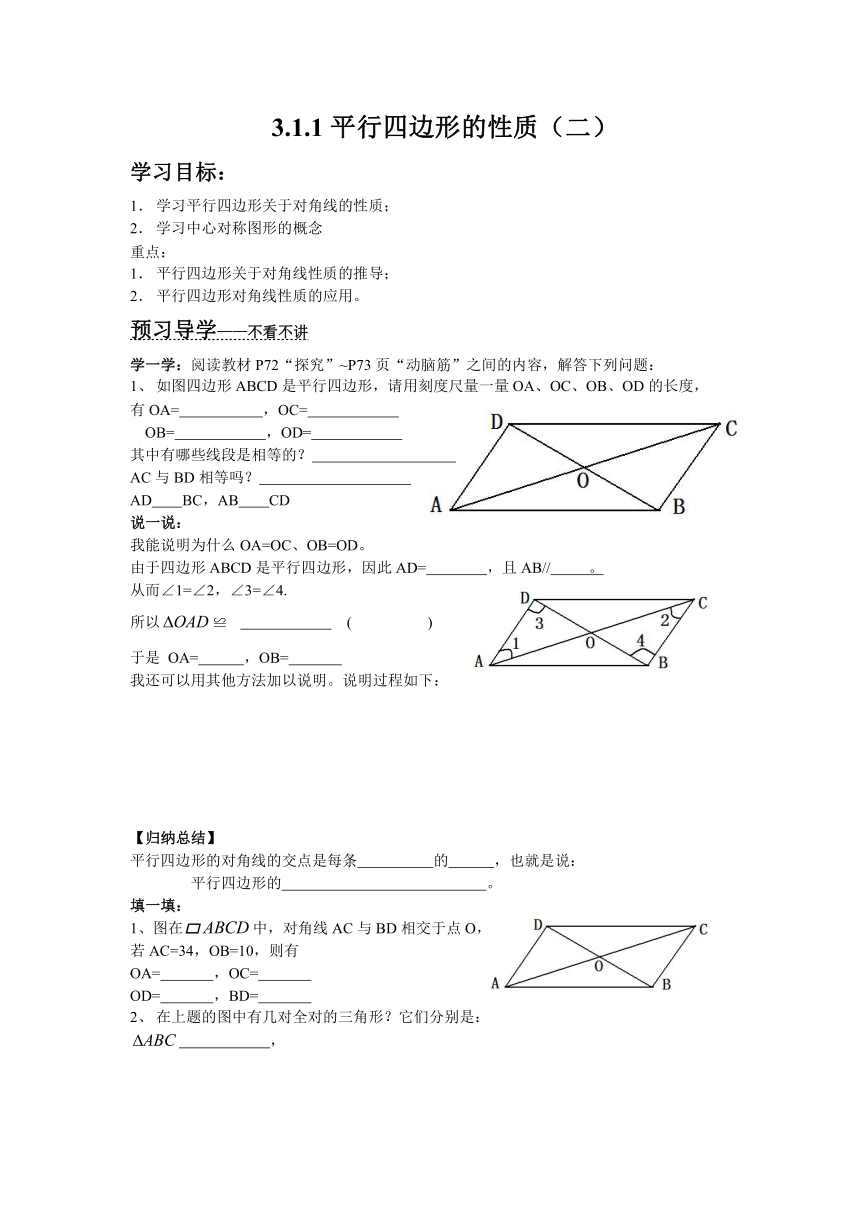
学一学：阅读教材P72“探究”~P73页“动脑筋”之间的内容，解答下列问题：
如图四边形ABCD是平行四边形，请用刻度尺量一量OA、OC、OB、OD的长度，
有OA= ，OC=
OB= ，OD=
其中有哪些线段是相等的？
AC与BD相等吗？
AD BC，AB CD
说一说：
我能说明为什么OA=OC、OB=OD。
由于四边形ABCD是平行四边形，因此AD= ，且AB// 。
从而∠1=∠2，∠3=∠4.
所以≌ ( )
于是 OA= ，OB=
我还可以用其他方法加以说明。说明过程如下：
【归纳总结】
平行四边形的对角线的交点是每条 的 ，也就是说：
平行四边形的 。
填一填：
1、图在中，对角线AC与BD相交于点O，
若AC=34，OB=10，则有
OA= ，OC=
OD= ，BD=
在上题的图中有几对全对的三角形？它们分别是：
，
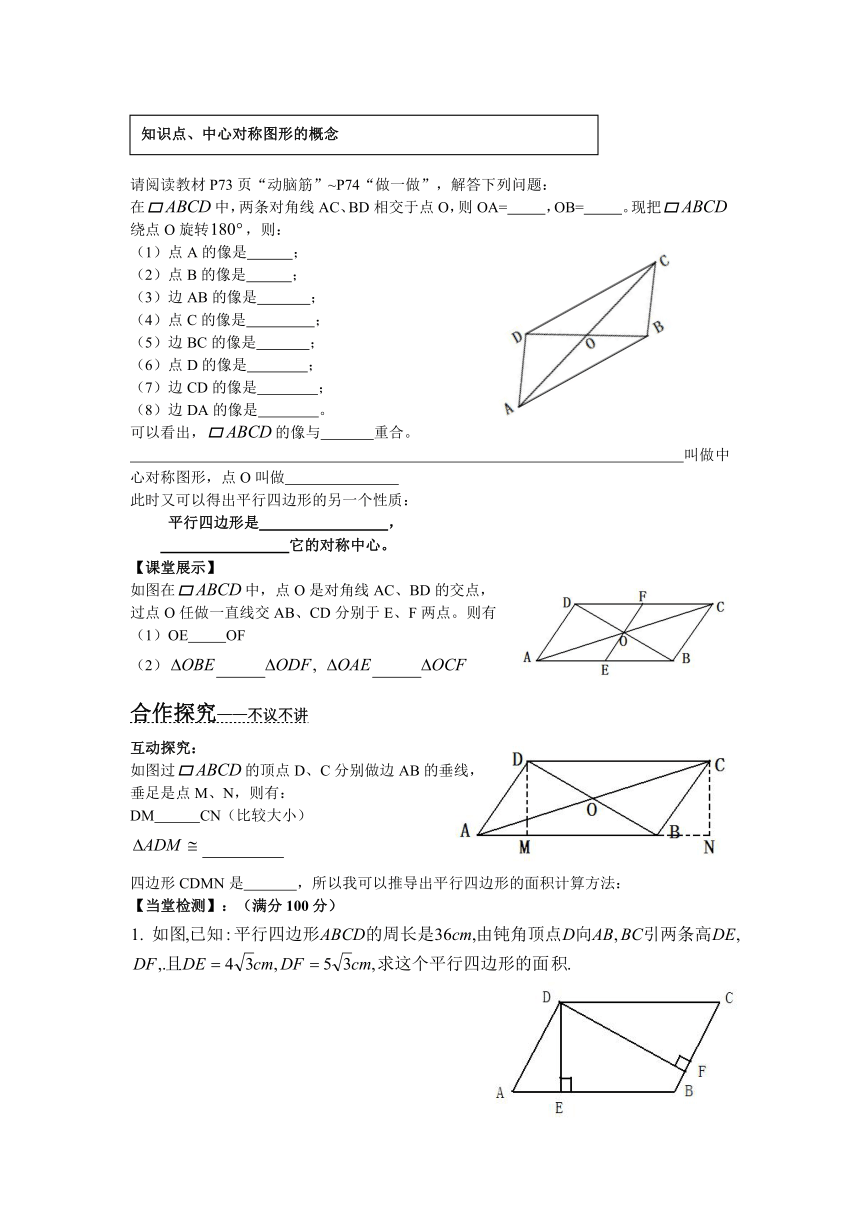
请阅读教材P73页“动脑筋”~P74“做一做”，解答下列问题：
在中，两条对角线AC、BD相交于点O，则OA= ，OB= 。现把绕点O旋转，则：
（1）点A的像是 ；
（2）点B的像是 ；
（3）边AB的像是 ；
（4）点C的像是 ；
（5）边BC的像是 ；
（6）点D的像是 ；
（7）边CD的像是 ；
（8）边DA的像是 。
可以看出，的像与 重合。
叫做中心对称图形，点O叫做
此时又可以得出平行四边形的另一个性质：
平行四边形是 ，
它的对称中心。
【课堂展示】
如图在中，点O是对角线AC、BD的交点，
过点O任做一直线交AB、CD分别于E、F两点。则有
（1）OE OF
（2）
合作探究——不议不讲
互动探究：
如图过的顶点D、C分别做边AB的垂线，
垂足是点M、N，则有：
DM CN（比较大小）
四边形CDMN是 ，所以我可以推导出平行四边形的面积计算方法：
【当堂检测】：（满分100分）
3．1．2 中心对称图形（续）
学习目标：
进一步加强学习中心对称图形的相关概念；
学习中心对称图形的性质；
能画出中心对称图形的对称中心。
重点：
归纳中心对称图形的性质；
归纳具有中心对称性质的简单几何图形和部分现实生活中的例子。
预习导学——不看不讲
学一学：阅读教材P75页~P76页“说一说”的内容，解答下列问题：
1、教材中“观察”部分第1个问题，是中心对称图形的是 ，不是中心对称图形的是 。
2、教材中“观察”部分第2个问题，是中心对称图形的是 ，不是中心对称图形的是 。
3、 此时称点E和点F关于点O对称， 一对对应点。
4、两个对应点之间通常用 连接（实线、虚线），对就点的连线一定会过 。
做一做：
如图1—1试画出点M关于点O成中心对称的对称点N。
已知点A、B是关于点O成中心对称的两点，请在图2—1中确定这一点O。
3、在下图3—1中请画出线段EF关于点O成中心对称的线段AB。
【归纳总结】
1、我能说出中心对称图形的性质有（说得越多越有成就感）：
2、要判断一个图形是否是中心对称图形，首先要确定 ，再围绕这一点旋转角度
为 后，看它是否与原图形重合，若重合则该图形是 ，若旋转后的图形与原图形不重合，则该图形不是 。
【课堂展示】
目前我们所学过的基本图形中是中心对称图形的有（我能举出很多的例子）：
图形名称 对称中心 图例
平行四边形 对角线交点
线段
。。。。。。 。。。。。。 。。。。。。。
我们所学过的汉字中是中心对称图形的有： ；
我们所学过的英文字母中是中心对称图形的有： ；
我们所学过的数字中是中心对称图形的有： ；
我们所学过的运算符号中是中心对称图形的有： ；
扑克牌中是中心对称图形的扑克牌有： ；
麻将牌中是中心对称图形的麻将牌有： ；
在生活中我还可以举出更多的是中心对称图形的例子： 。
【当堂检测】：（第1、2小题各40分，第3小题每画一个图形加10分）
请确定下列各图形的对称中心
2、请画出四边形ABCD关于点O成中心对称的图形
3、我还可以设计出一些是中心对称的图形
3．1．3 平行四边形的判定（一）
学习目标：
学习平行四边形的两种判定方法；
能结合图形用几何语言说出平行四边形的判定过程。
重点：
能用平行四边形的判定方法解决简单的问题。
预习导学——不看不讲
学一学：阅读教材P77页“动脑筋”的内容，解答下列问题：
称为平行四边形。
2、结合图形1用定义可以说明四边形ABCD是平行四边形，
如图在四边形ABCD中
有：AB//
//AD 则
四边形ABCD是平行四边形
3、如图2，AC、BD是四边形ABCD的对角线，
交点是点O，且OA=OC，OB=OD。
则四边形ABCD是平行四边形
解：由于在和中
≌ ( )
从而 （ ）
于是 AB// （ ）
同理 AD// 。
所以四边形ABCD是 。
【归纳总结】
平行四边形的一种判定方法：
结合图3，说明四边形ABCD是平行四边形
在四边形ABCD中
OA=
=OD
则四边形ABCD是平行四边形。 图3
学一学：阅读教材P78页“动脑筋”内容，解答下列问题。
如图4在四边形ABCD中，AB=CD，且AB//CD。
求证：四边形ABCD是平行四边形。
【归纳总结】
平行四边形的又一种判定方法：
结合图形5，说明四边形ABCD是平行四边形
方法一：在四边形ABCD中，有
AB=
AB//
则四边形ABCD是 。
方法二：在四边形ABCD中，有
AD=
AD//
则四边形ABCD是 。
【课堂展示】
1、已知：如图6，在的对角线AC上有两点E、F，且AE=CF，对角线BD上有两点M、N，且BM=DN。
求证：四边形EMFN是平行四边形。
已知：如图7，在的边AB、CD上分别取一个点E、F，使得AE=AB，DF=CD，连接BF、DE。
求证：（1）四边形BFDE是平行四边形；
（2）BF=DE。
【当堂检测】：（满分100分）
已知：如图，把的中线AD延长至点E，使得DE=AD，连结EB、EC。
求证：四边形ABEC是平行四边形。
3．1．3 平行四边形的判定（二）
学习目标：
进一步学习平行四边形的判定方法；
将平行四边形的判定方法进行整理。
重点：
平行四边形判定方法的运用；
平行四边形判定方法的推导。
预习导学——不看不讲
学一学：阅读教材P80页“动脑筋”的内容，解答下列问题：
如图在四边形ABCD中，AB=CD，AD=BC，
求证：四边形ABCD是平行四边形
证法一：（我可以用“一组对边平行且相等的四边形
是平行四边形”加以证明）
证法二：（我还可以用定义“两组对边分别平行的四边形是平行四边形”加以证明）
【归纳总结】
平行四边形的又一种判定方法：
两组对边分别 的四边形是平行四边形。
议一议：
两组邻边分别相等的四边形是平行四边形吗？我可以用一个图形来加以说明：
一组对边相等，另一组对边平行的四边形一定是平行四边形吗？我可以用一个图形来加以说明：
目前我们学习了下面几种平行四边形的判定方法：
（1）两组对边分别 的四边形是平行四边形；
（2）两组对边分别 的四边形是平行四边形；
（3）一组对边 的四边形是平行四边形；
（4）对角线 的四边形是平行四边形。
这几种方法我都可以结合图形用几何语言加以说明：
如图1，在四边形ABCD中，
AB// ，AD//
则四边形ABCD是平行四边形。
如图1，在四边形ABCD中，
AB= ， =
则四边形ABCD是平行四边形。
（3） 如图1，在四边形ABCD中， 或者 如图1，在四边形ABCD中，
AB// ，AB= AD// ，AD=
则四边形ABCD是平行四边形 则四边形ABCD是平行四边形。
如图2，在四边形ABCD中，对角线AC、BD
相交于点O，
OA= ，OD=
或：OA= ，OB=
四边形ABCD是平行四边形。
【课堂展示】
如图， 是由四个全等的三角形拼成的，
请找出其中所有的平行四边形，并且说明理由。
【当堂检测】：（每小题50分，共100分）
1、如图3，在四边形ABCD中，AB=DC，BC=AD，E、F分别是边AB、CD上的点，且AE=AB，DF=DC。请找出图3中所有的平行四边形，并且说出理由。
如图4，在四边形ABCD中，。
求证：四边形ABCD是平行四边形。
3．1．4 三角形的中位线
学习目标：
记忆三角形的中位线概念；
理解三角形中位线性质定理；
能理解三角形中位线性质定理的推导
重点：
结合图形能用几何语言描述三角形中位线性质定理；
用三角形中位线性质定理解决一些简单的实际问题。
预习导学——不看不讲
学一学：阅读教材P82页的内容，解答下列问题：
叫做三角形的中位线。
2、一个三角形有 条中位线，
我能在图1的三角形中画出三角形的中位线。
3、在图2中，我量线段EF= ，AB= ，
我可以猜测出线段EF与AB的关系式是 。
我还可以猜测出线段EF与AB的位置关系是： 。
学一学：阅读教材P82~P83例4上方的内容，解答下列问题：
如图3，点E、F分别是边AC、BC上的中点，
求证：EF=AB，EF//AB。
证明：将绕点F旋转，设点E的像
为点G，易知点C的像是点 ，点F的像是点 ，
且E、F、G在同一条直线上。
又因为旋转不改变图形的 ，所心有
BG= = ，GF= ，=
则CE// 。 （ ）
即 AE//
又AE=
所以四边形 是平行四边形。（ ）
所以EG= ，EG// 。 （平行四边形的 ）
又因为EF=FG
所以EF= = ，EF// 。
【归纳总结】
三角形中位线性质定理：
三角形的中位线平行于 ，并且等于 。
【课堂展示】
填一填：
如图5，点E、F、H分别是三边上的中点，则有：
（1）的中位线有
（2）HF// ，HF= = =
（3）HE// ，HE= = =
（4）EF// ，EF= = =
2、在图5中，有几个平行四边形？它们分别是
3、如图6，顺次连结四边形ABCD各边中点E、F、H、M，得到的四边形EFHM是平行四边形吗？为什么？
【当堂检测】：（每小题50分，共100分）
1、如图7，设四边形EFHM的两条对角线EH、FM的长分别为12、10，A、B、C、D分别是边EF、FH、HM、ME的中点，求的周长。
如图8，已知三边AB=18，BC=10，AC=16，
则有：
（1）EF= ，HF= ，HE= ；
（2）的周长是
（3）图形中有 对全等的三角形，它们分别是
；
（4）图形中有 个平行四边形，它们分别是
；
（5）的面积关系是 。
3．2．1 菱形的性质
学习目标：
记忆菱形的定义；
记忆菱形的性质；
能区别菱形与平行四边形；
菱形的面积计算公式。
重点：
菱形的作图；
菱形的性质的应用。
预习导学——不看不讲
学一学：阅读教材P88“观察”的内容，回答下列问题：
1、 的四边形叫做菱形。
2、菱形也是平行四边形，是特殊的平行四边形，特殊在于它是一组邻边 的平行四边形。
3、我也能在下方画几个菱形的图形：
说一说：
菱形的性质：
（1）菱形是 图形，对称中心是 ；
（2）菱形的 相等， 相等，对角线 ；
（3）菱形的四条边 。
我可以结合图1用几何语言将菱形的性质加以描述：
（1）菱形ABCD是中心对称图形，对称中心是点 ；
（2）菱形ABCD中，AB= ，AD= ；
（3）菱形ABCD的对角线AC、BD相交于点O，则
OA= = ；OD= = ；
（4）菱形的四边 ，即：AB= = = 。
学一学：阅读教材P89“动脑筋”的内容，回答下列问题：
菱形的性质：
（1）菱形是 图形，它的对称轴是 ；
（2）菱形的 互相垂直，并且每一条对角线 。
我可以结合图形2，将菱形的性质加以描述：
（1）菱形ABCD是轴对称图形，它的对称轴有 条，
是直线 ；
（2）菱形的对角线 ；
（3）在菱形ABCD中，
= = =；
= = = == ；
= = = == ；
= = = =
（4）在图形2中，有 对全等的三角形，它们分别是
学一学：阅读P90的内容，解答下列问题：
1、在菱形ABCD中，对角线AC、BD将菱形分成 对全等
的三角形，它们分别是
；
2、菱形ABCD面积计算公式是： 。
【课堂展示】
如图4，菱形ABCD的两条对角线AC、BD长度分别为8cm，
6cm.
求菱形ABCD的面积和周长。
【当堂检测】：(每小题50分，共100分)
已知菱形ABCD的两条对角线的交点为O，AB=13，OA=5。
求菱形ABCD的两条对角线的长度以及它的面积。
2、如图5，菱形ABCD的边长为4，，
求菱形ABCD的两条对角线的长度以及它的面积。
3．2．2 菱形的判定
学习目标：
记忆菱形的三种判定方法；
会画菱形
重点：
菱形判定方法的应用。
预习导学——不看不讲
学一学：阅读教材P91页的内容，解答下列问题：
1、菱形的两条对角线 ；
2、根据菱形两条对角线相互间的关系性质，我也能在下方空白处画一个标准的菱形：
我还能说出上述画的图形一定是菱形的道理：
【归纳总结】
菱形的判定方法：
对角线 的四边形是菱形。或者说，对角线 的平行四边形是菱形。
议一议：
对角线互相垂直的四边形是菱形，对吗？我能用一个图形加以说明。
对角线互相平分的四边形是菱形，对吗？我能用一个图形加以说明。
阅读教材P92页“做一做”的内容，解答下列问题；
1、菱形的第三种判定方法： 的四边形是菱形。
2、我能用几何语言来描述菱形的第三种方法：
如图2，四边形ABCD中，
AB= = =
则四边形ABCD是菱形。
目前我们学习了这些菱形的判定方法：
1、一组 的平行四边形是菱形；
2、对角线 的四边形是菱形；
3、四条边 的四边形是菱形。
【课堂展示】
如图3，已知菱形ABCD的周长为16，，求：
菱形的其它几个内角的度数；
菱形的边长；
菱形的对角线长；
菱形的面积。
【当堂检测】：（每1小问25分，共计100分）
如图4，四边形ABCD是菱形，，AC=16，求：
菱形四个角的度数；
BD的长；
菱形的周长；
菱形的面积。
3．3矩形（一）
学习目标：
记忆矩形的定义；
能结合图形说出矩形的性质；
记忆矩形的判定方法。
重点：
利用矩形的性质和判定方法解决一些简单的实际问题。
预习导学——不看不讲
学一学：阅读教材P95“观察”~P97“说一说”上方的内容，解决下列问题：
在现实生活中我还能举出更多是矩形的例子：
叫做矩形，也称为
3、从矩形的定义可以看出，矩形是特殊的平行四边形，特殊在于它有一个角是
（ ）
从上可得， 都是直角的四边形是矩形。
由此容易得出：矩形的四个角都
4、结合图形1我能说出矩形的一些性质：
（1）边：AB= ，AD=
（2）角：= = = =
（3）对角线：AC= ，
OA= = =
（4）在图1中有 对全等的三角形，它们分别是
；
（5）图1中有 个等腰三角形，它们分别是
学一学：阅读教材P97“说一说”~P98内容，解答下列问题：
1、结合图2，向同桌我能说出“对角线相等且互相平分的四边形是矩形。或者说，对角线相等的平行四边形是矩形”。并能写下来。
【归纳总结】
矩形的判定方法：
1、有一个角是 的平行四边形是矩形；
2、四个角都是 的四边形是矩形；
3、对角线 的四边形是矩形。或者说，对角线 的平行四边形是矩形
【课堂展示】
有三个角是直角的四边形是矩形，对吗？
我能用一个图形加以说明。
有二个角是直角的四边形是矩形，对吗？
我能用一个图形加以说明。
有一个角是直角的四边形是矩形，对吗？
我能用一个图形加以说明。
对角线相等的四边形是矩形，对吗？
我能用一个图形加以说明。
如图3，在中，它的两条对角线相交于点O。
如果是矩形，
试问：是什么样的三角形？
如果是等腰三角形，其中OA=OD，
试问：是矩形吗？
【当堂检测】：（每一小问25分，共计100分）
如图4，在矩形ABCD中，，且AC=4。求：
矩形的对角线长；
矩形的各边长；
矩形的周长；
矩形的面积。
3．3矩形（二）
学习目标：
能理解矩形是轴对称图形，并能说出矩形的对称轴；
进一步加强对矩形性质和判定的理解与应用。
重点：
矩形性质和判定在实际例子中的应用。
预习导学——不看不讲
学一学：阅读教材P99页“动脑筋”的内容，解答下列问题：
1、对称性：矩形既是 ，它的对称轴是 ；
又是 ，它的对称中心是 。
2、我能在下图1中画出矩形ABCD的对称轴，标出对称中心。
学一学：阅读教材P100的内容，解答下列问题：
如图2，矩形ABCD被它的两条对称轴EF、MN分成四个小四边形，它们都是矩形吗？它们全等吗？为什么？
直线MN、EF有何位置关系？
将直线MN、EF同时绕点O旋转同一方向、
同一个角度后，这两条直线能将矩形分成几个
四边形？这些四边形是全等的吗？能将矩形分
成几个三角形吗？分成的三角形是全等的吗？
4、请你连结ME、EN、NF、FD后，发现四边形MENF是什么样的四边形？请说明理由。
【课堂展示】
当堂检测（每小题50分，共计100分）
从菱形两条对角线的交点分别向各边引垂线。
求：连接各垂足的四边形是矩形。
已知：
求证：
3．4 正方形
学习目标：
理解正方形的性质与判定方法；
能画出正方形的对称轴，能标记出正方形的对称中心
重点：
1．利用正方形的性质和判定解决一些简单的实际问题。
预习导学——不看不讲
学一学：阅读教材P102~P103的内容，解决下列问题：
1、我能说出现实生活中是正方形的例子：
的矩形叫做正方形。或者说，
的平行四边形叫做正方形。
平行四边形、菱形、矩形、正方形四者之间的关系：
（ ） （ ）
（ ） （ ）
【归纳总结】
正方形的性质：
1、边、角：正方形的四条边都 ，四个角都是 ；
2、对角线：正方形的对角线 ，且 ；每条对角线平分 ；
3、对称性：正方形是 图形，它的对称中心是 ；
正方形是 图形，它的对称轴有 条，分别是 。
我能结合图1说出正方形的性质：
1、边：AB= = =
2、角： = = =
= =。。。。。。。=
3、对角线：AC= ，OA= = =
4、对称性：对称中心是点 ，
我能在图1中画出正方形的对称轴。
5、图1中有 个等腰直角三角形，它们分别是
，
其中这些三角形是全等三角形：
。
【课堂展示】
已知一个正方形的边长是4，试求它的对角线长。
已知一个正方形对角长为4，试求它的边长和面积。
【当堂检测】：（每小题10分，共计100分）
1．正方形的四条边都 ，四个角都是 ，对角线 。
2．如果一个四边形是菱形，又是矩形，那么这个四边形一定是 。
5．下列命题，正确的有（ ）
①对角线相等的菱形是正方形 ②四条边都相等的四边形是正方形 ③四个角相等的四边形是正方形 ④对角线互相垂直的矩形是正方形 ⑤对角线垂直且相等的四边形是正方形
A ①② B ②③ C ①④ D ③⑤
6. 已知正方形的一边长为1cm，则它的周长为____，面积为______，对角线长为_____；
7. 已知正方形的对角线长为2cm，则它的边长为_____;
8. 正方形具有而菱形不一定具有的性质是（ ）
（A）四条边相等 （B）对角线互相垂直且平分
（C）对角线平分一组对角（D）对角线相等
9. 正方形具有而矩形不一定具有的性质是（ ）
（A）四个角相等 （B）对角线互相垂直且平分
（C）对角线相等 （D）对角互补
10．（2009.郴州）1.如图，E是正方形ABCD对角线AC上的一点，求证：BE=DE
3．5 梯形（一）
学习目标：
记忆梯形的有关概念、结构；
梯形的分类；
等腰梯形的概念、性质、判定
重点：
等腰梯形的性质和判定的记忆；
等腰梯形的性质、判定的应用。
预习导学——不看不讲
学一学：阅读教材P105“说一说”的内容，解答下列问题：
我还能说出日常生活中有这些物体的形状中包含梯形：
的四边形叫做梯形，
叫做梯形的底（通常把 叫做上底，
叫做下底）， 叫做梯形的腰， 叫做梯形的高。
3、在图1中，我能把梯形的结构标识在图形上。
（ ）
（ ） （ ） （ ）
（ ）
4、 叫做等腰梯形，
叫做直角梯形。
5、我也能在下方空白处画出等腰梯形和直角梯形：
　　　　　　　　　　　　　　　　　　　　　　　　　　　）
　　　　　　　　　　　　　　　　　　　　　　　　
（ ）　　　　　（
　　　　　　　（　　　　　　）　　　　（
　　　　　　　　　　　　　　　　　　　　　　　　　　）
学一学：阅读教材Ｐ106“探究”~P108的内容，解答下列问题：
1、等腰梯形的性质：
（1）等腰梯形在同一底上的 相等；
（2）等腰梯形的两条对角线 ；
（3）对称性：等腰梯形是 图形，它的对称轴有 条，是
（4）等腰梯形在同一腰上的两个角 。
2、我能结合图2说出等腰梯形的性质：
在梯梯形ABCD中，
（1）角：
（2）边：AD=
（3）对角线： =
（4）OA= ，OC=
（5）在图2中，有 对全等的三角形，它们分别是
（6）在图2中，有 个等腰三角形，它们分别是
（7）我能在图2 中画出等腰梯形ABCD的对称轴。
3、在图3中，过点D、C分别向AB作垂线，垂足分别
为点E、F，则图3中有 个全等的三角形，它们分
别是 ，CD= ，AE= 。
梯形ABCD的面积是：
4、我能说出等腰梯形的判定方法：
【课堂展示】
1、如图4，在等腰梯形ABCD中，AD//BC，DE是梯形的高。
（1）BE与两底AD、BC有何关系？
（2）设AD=6，BC=8，AE=5，试求：腰AB的长
和梯形ABCD的面积。
【当堂检测】：（每小题25分，共100分）
1、等腰梯形的上底与高相等，下底是上底的3倍，则下底的一个底角= ___。
2、若等腰梯形的钝角为120°，上底长为5，腰长为4，则该梯形的面积等于__。
3、一直角梯形的一腰长与下底的长都为6cm，且它们的夹角为60 °，则它的上底长为___
4、四个内角的度数比是2：2：1：3，则此四边形是（ ）。
（A)任意四边形 (B)任意梯形
(C)等腰梯形 (D)直角梯形
3．5 梯 形（二）
学习目标：
能画一个等腰梯形；
进一步加强对等腰梯形性质和判定的学习；
归纳在等腰梯形中作辅助线的几种作法。
重点：
1．在等腰梯形中作辅助线的几种方法和作用；
2．对等腰梯形性质和判定的应用。
预习导学——不看不讲
学一学：阅读教材P109~P111的内容，解答下列问题：
1、我能用两种以上的不同方法画一个等腰梯形：
2、在处理等腰梯形的相关问题时，一般有以下几种作辅助线的方法：
方法一：
过上底端点向下底作高。
我认为这种作辅助线的方法可以解决以下问题：
方法二：
作对角线。
我认为这种作辅助线的方法可以解决以下问题：
方法三：
过一端点作腰的平行线。
我认为这种作辅助线的方法可以解决以下问题：
方法四：
延长两腰。
我认为这种作辅助线的方法可以解决以下问题：
我还能说出其它的作辅助线的方法及其作用。
【课堂展示】
1、如果梯形ABCD对角线的交点O与同一底的两个端点的距离相等，那么它是等腰梯形吗？为什么？
2、如图6，已知梯形ABCD的对角线AC=BD。
求证：梯形ABCD是等腰梯形。
【当堂检测】：（第1小题20分，2、3小题各40分，共100分）
1、梯形ABCD中,AD∥BC,AC、BD交于O点，则梯形中共
有（ ）对面积相等的三角形。
（A）2 （B）3 （C）4 （D）5
2、 已知梯形ABCD中，AB∥CD，∠A=40° ∠ B:∠ C:∠ D=3:6:7，求∠ D的度数。
3、如图8，梯形 ABCD中，AB∥CD，AC平分∠ DAB，且AC⊥BC, ∠DAB=60°梯形周长为20，求AD的长
3．6 多边形的内角和与外角和（一）
学习目标：
知道多边形的定义；
知道多边形的结构；
记忆多边形的内角和算公式。
重点：
多边形内角和计算公式的推导；
多边形内角和计算公式的应用。
预习导学——不看不讲
学一学：阅读教材P112~P113的内容，解答下列问题：
1、三角形的内角和为 度。
2、四边形的任一条对角线可以把四边形分成 个三角形，所以一个四边形的内角和
为 度。
3、 叫做多边形，
叫做多边形的边， 叫做多边形的顶点， 叫做多边形的对角线，
叫做多边形的内角。
4、多边形按凹凸形状可以分为 两类。
5、n边形有 条边，有 个顶点，有 个内角，有 条对角线。
学一学：阅读教材P113“探究”~P114的内容，解答下列问题：
1、五边形的内角和为 度。我有几种推导五边形的内角和的方法。
方法一：如图1，连结两条对角线AD、AC 方法二：如图2，连结一条对角线AC，
把五边形分成三个三角形； 把五边形分成一个四边形和一个三角形
方法三：如图3，在五边形内任取一点O，
连接OA、OB、OC、OD、OE
把五边形分成五个三角形。
我还有其它的不同方法。
2、n边形的内角和为 度。
n边形的内角和我可以按类似于求五边形内角和的
方法一可以求出，
我也可以按方法三的思路求出。
结合图4，请将你的方法告诉同桌，好吗。
【课堂展示】
1、九边形的内角和是多少度？
2、正十二边形的内角都相等，它的每一个内角是多少度？
【当堂检测】：（第1、2小题各30分，第3小题40分，共计100分）
1、如果一个多边形的内角和是1440度，试求这个多边形的边数。
2、若正n边形的一个内角是144度，试求 n的值。
3、在四边形ABCD中，∠A=120度，∠B：∠C：∠D = 3：4：5，
求∠B，∠C，∠D的度数。
3．6多边形的内角和与外角和（二）
学习目标：
记忆多边形的外角和；
了解四边形的不稳定性在实际生活中的运用。
重点：
多边形外角和的推导；
多边形外角和的应用。
预习导学——不看不讲
学一学：阅读教材P115“说一说”的内容，解答下列问题：
1、三角形的外角和为 度；
2、 叫做多边形的外角；
3、多边形的每一个内角都有 个外角。多边形的一个内角与它的一个外角的和为 度
4、 叫做多边形的外角和。
5、如图1，
在五边形ABCDE中，的外角为 和
（1）互为 角，= ；
（2）= 度；
（3）五边形ABCDE的内角和为 度；
（4）五边形ABCDE的外角和为 度。
学一学：阅读教材P115“探究”的内容，解答下列问题：
1、四边形的内角和为 度；
2、四边形的外角和为 度；
3、边形（的内角和为 度；
4、边形（的外角和为 度。多边形的外角和是一个定值，它与多边形的边数无关。
【归纳总结】
任意多边形的外角和等于 度。
【课堂展示】
1、一个多边形的内角和等于它外角和的6倍，它是几边形？
学一学；阅读教材P116“说一说”的内容，解答下列问题：
1、 叫做正多边形。
2、在平面内，边都相等的多边形是正多边形，对吗？我能用图形加以说明。
在平面内，角都相等的多边形是正多边形，对吗？我能用图形加以说明。
4、正六边形的内角和是 度，它的每一个内角是 度，它的外角和是 度，它的每一个外角是 度。
学一学：阅读教材P116“动脑筋”，解答下列问题；
1、 叫做四边形的不稳定性。
2、我能说出在现实生活中利用四边形的不稳定性的例子：
【当堂检测】：（每小题25分，共计100分）
1、一个多边形的每一个外角都等于45°，这个多边形是几边形？它的每一个内角是多少度？
2、正十二边形的每一个内角是多少度？每一个外角是多少度？
3、画两个菱形，使它们的边长都为2cm.
4、如果一个多边形的每一个外角都等于它相邻的内角，那么这个多边形的每一个外角是多少度？这个多边形是几边形？
第三章总复习单元测试（一）
班次 姓名
一、选择题（每小题3分，共计18分）
1.若一个多边形的内角和等于，则这个多边形的边数是（ ）
A．5 B．6 C．7 D．8
2. 如图，四边形的对角线互相平分，要使它变为矩形，需要添加的条件是（ ）
A． B．
C． D．
3.在平行四边形中，，那么下列各式中，不能成立的是（ ）
A． B． C． D．
4.把长为8cm的矩形按虚线对折，按图中的虚线剪出一个直角梯形，找开得到一个等腰梯形，剪掉部分的面积为6cm2，则打开后梯形的周长是（ ）
A．cm B．cm C．22cm D．18cm
5.如图，方格图中小正方形的边长为1．将方格图中阴影部分图形剪下来，再把剪下的阴影部分重新剪拼成一个正方形，那么所拼成的这个正方形的边长等于（ ）．
（A） (B) 2 （C） （D）
6.一个正方形的对称轴共有（ ）
A．1条 B．2条 C．4条 D．无数条
二、填空题（每小题3分，共计33分）
7.从下列图中选择四个拼图板,可拼成一个矩形,正确的选择方案为 ． (只填写拼图板的代码)
8. 如图，在中，分别是的中点，若，则 cm．
9. 如图，菱形的边长为2，，则点的坐标为 ．
10.如图，在中，分别是的中点，若，则的长是 ．
11.如图，菱形中，是对角线的交点，，，则 cm．
12.如图，在四边形中，是对角线的中点，分别是 EMBED Unknown 的中点，，则的度数是 ．
13.如图(1)是一个等腰梯形，由6个这样的等腰梯形恰好可以拼出如图(2)所示的一个菱形.对于图(1)中的等腰梯形，请写出它的内角的度数或腰与底边长度之间关系的一个正确结论： ．
14. 如图，已知P是正方形ABCD对角线BD上一点，且BP = BC，则∠ACP度数是 ．
15. 如图，要测量A、B两点间距离，在O点打桩，取OA的中点 C，OB的中点D，测得CD=30米，则AB=______米．
16.如图，在中，分别是的中点，且，则．
17.边长为５cm的菱形，一条对角线长是6cm，则另一条对角线的长是 .
三、计算题（18小题4分，19小题5分，共9分）
18. 如图，在梯形中，，，，，，求的长．
解：
19.如图，在平行四边形中，，求的度数．
解：
四、证明题（每小题10分，共计30分）
20.如图，在等腰梯形中，，是的中点，求证：．
21.如图，在菱形中，°，过点作且与的延长线交于点．
求证：四边形是等腰梯形．
22.如图所示，已知等腰梯形ABCD中，AD∥BC，AB=DC，AC与BD相交于点O．请在图中找出一对全等的三角形，并加以证明．
SHAPE \* MERGEFORMAT
五、复合题（10分）
23.如图，在△ABC中，D，E分别是AB，AC的中点，BE＝2DE，延长DE到点F，使得EF＝BE，连接CF．
求证：四边形BCFE是菱形；
解：
第三章总复习单元测试（二）
班次 姓名
一、选择题（每小题3分，共计24分）
1. 如图，在平行四边形中，是延长线上的一点，若，则的度数为（ ）
A． B． C． D．
2.如图所示，有一张一个角为的直角三角形纸片，沿其一条中位线剪开后，不能拼成的四边形是（ ）
A．邻边不等的矩形 B．等腰梯形
C．有一角是锐角的菱形 D．正方形
3.某商店出售下列四种形状的地砖：①正三角形；②正方形；③正五边形；④正六边形．若只选购其中一种地砖镶嵌地面，可供选择的地砖共有（ ）．
A．4种 B．3种 C．2种 D．1种
4. 如图，将边长为8cm的正方形纸片ABCD折叠，使点D落在BC边中点E处，点A落在点F处，折痕为MN，则线段CN的长是（ ）．
A．3cm B．4cm
C．5cm D．6cm
5.为了让州城居民有更多休闲和娱乐的地方，政府又新建了几处广场，工人师傅在铺设地面时，准备选用同一种正多边形地砖．现有下面几种形状的正多边形地砖，其中不能进行平面镶嵌的是（ ）
A．正三角形 B．正方形 C．正五边形 D．正六边形
6. (多选)如图，已知梯形中，，，相交于点，，则下列说法正确的是（ ）
A．梯形是轴对称图形 B．
C．梯形是中心对称图形 D．平分
7.科技馆为某机器人编制一段程序，如果机器人在平地上按照图中所示的步骤行走，那么该机器人所走的总路程为（　　）
A．6米　　 B．8米　　 C．12米　 D．不能确定
8.顺次连接等腰梯形四边中点所得四边形是（ ）
A．菱形 B．正方形 C．矩形 D．等腰梯形
二、填空题（每小题3分，共计24分）
9. 如图，正方形的边长为4cm，则图中阴影部分的面积为 cm2．
10. 如图，在等腰梯形ABCD中，AD∥BC，AE∥DC，AB=6cm，则AE= cm.
11.己知菱形ABCD的边长是6，点E在直线AD上，DE＝3，连接BE与对角线AC相交于点M，则 的值是 ．
12.一幅图案．在某个顶点处由三个边长相等的正多边形镶嵌而成．其中的两个分别是正方形和正六边形，则第三个正多边形的边数是 ．
13. 如图，矩形中，cm，cm，点为边上的任意一点，四边形也是矩形，且，则 ．
14.已知菱形的两对角线长分别为6cm和8cm，则菱形的面积为 cm2．
15.如图，菱形ABCD的两条对角线分别长6和8，点P是对角线AC上的一个动点，点M、N分别是边AB、BC的中点，则PM+PN的最小值是_____________．
16.如图，矩形纸片ABCD中，AD=9，AB=3，将其折叠，使点D与点B重合，折痕为EF，那么折痕EF的长为________．
三、证明题（每小题12分，共计24分）
17.如图，在平行四边形中，分别为边的中点，连接．
（1）求证：．
（2）若，则四边形是什么特殊四边形？证明你的结论．
18.已知：如图，点是正方形的边上任意一点，过点作交的延长线于点．求证：．
四、复合题（每小题14分，共计28分）
19．如图，在△ABC 中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的角平分线于点E，交∠BCA的外角平分线于点F．
（1）求证：EO=FO；
（2）当点O运动到何处时，四边形AECF是矩形？
并证明你的结论．
20．如图，在等腰Rt△ABC中，∠C=90°，正方形DEFG的顶点D在边AC上，点E、F在边AB上，点G在边BC上.
（1）求证AE=BF；
（2）若BC=cm，求正方形DEFG的边长.
知识点一、平行四边形的概念
知识点、中心对称图形的概念
知识点 平行四边形的判定方法
知识点一、三角形的中位线性质定理
知识点一、菱形的性质
知识点二、菱形的性质
知识点二、菱形的面积计算公式
知识点二、菱形的第三种判定方法
知识点一、矩形 的概念
矩形
平行四边形
知识点二、矩形的判定
知识点一、矩形的对称性
菱形
正方形
平行四边形
矩形
知识点一、梯形的相关概念
等腰梯形
梯形
四边形
直角梯形
知识点二、等腰梯形性质和判定
知识点一、多边形的概念
知识点二、多边形的内角和计算公式
知识点一、多边形的外角与外角和的概念
知识点二、多边形的外角和
知识点三、正多边形的概念
知识点四、四边形的不稳定性
O
A
D
C
B
3cm
3cm
C
A
E
D
B
O
(B)
A
D
x
y
C
A
B
C
E
D
C
F
D
B
E
A
P
B
C
D
A
P
B
C
M
N
A
A
B
C
D
AB
BB
CB
DB
D
A
B
C
E
D
B
A
O
C
A
B
C
D
F
E
A
B
E
C
D
1
A
D
O
C
B
开始
机器人站在点A处
向前走1米向左转30°
机器人回到点A处
结束
是
否
第9题图
A
B
C
D
A
D
C
E
F
G
B
D
A
B
C
P
M
N
C’
A
F
D
B
C
E
A
B
C
D
E
F
A
E
B
C
F
D
1
2
3