2013中考总结复习冲刺练:中考答题策略与技巧
文档属性
| 名称 | 2013中考总结复习冲刺练:中考答题策略与技巧 |  | |
| 格式 | zip | ||
| 文件大小 | 195.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-23 14:41:32 | ||
图片预览








文档简介
课件24张PPT。2013中考总结复习冲刺练:1.计算题
0指数;负指数;三角数值.
例:计算2.解不等式组解题步骤;数轴表示
例:解不等式组,并用数轴表示解集解:解① 得
解② 得①②所以不等式组的解集为在数轴上表示解集为3.解方程分式方程:去分母不漏乘,去括号注意负号;要注意验根格式.
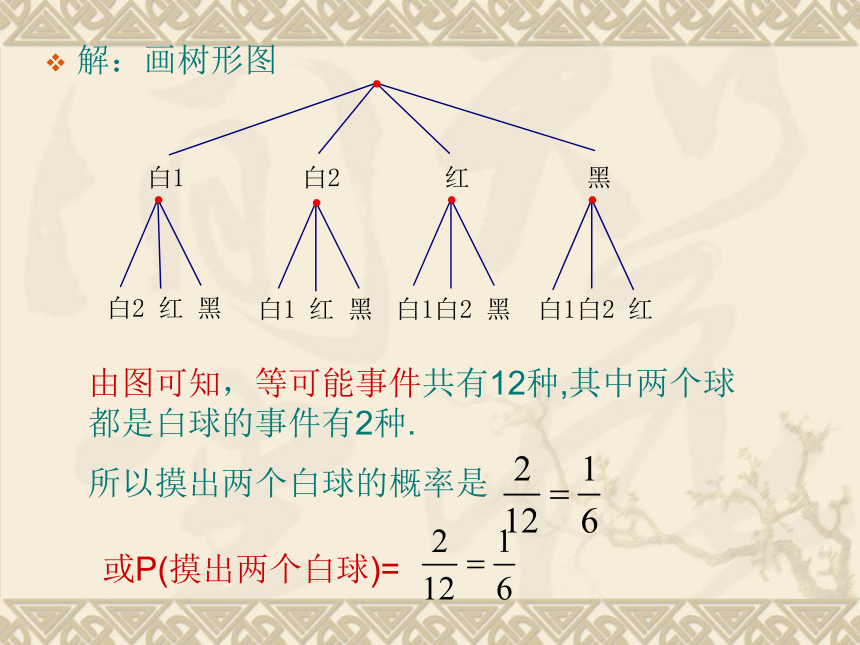
例:解分式方程解:分式两边同乘以得,解得,经检验何知 是方程的根 所以原方程的根是解二次方程(用因式分解法)解:原方程整理为即所以原方程的根为解二次方程(配方法)解:原方程整理为配方得原方程的根为所以即 或 解二次方程(公式法)解:原方程整理为因为原方程的根为所以4.统计问题树形图画法,等可能事件计算,概率表示.
例:口袋里装有2个白球1个红球1个黑球,它们的大小相同.现从中任取两个球,用树形图表示摸出两个白球的各种形况,并求它的概率.解:画树形图由图可知,等可能事件共有12种,其中两个球都是白球的事件有2种.所以摸出两个白球的概率是或P(摸出两个白球)=5.圆的切线证明半径+垂直=切线(判定定理)
例:如图,A,B是⊙O上的点,MN是过A点的直线,若∠AOB=2∠BAM.求证:MN切⊙O于点A.半径+垂直=切线(判定定理)
证明: 因为A,B是⊙O上的点,所以OA=OB,
所以,∠1=∠B,
在△ABO中,因为∠1+∠B+∠AOB=1800,
即,∠AOB=1800- 2∠1,
又因,∠AOB=2∠BAM
所以,1800-2∠1=2∠BAM
2∠BAM +2∠1=1800
∠BAM +∠1=900
即,OA⊥MN于A点,
又因OA是⊙O的半径
所以,MN切⊙O于点A6.证明三角形全等基本格式
在△ABC与△DEF中
因为 AB=DE
∠B=∠E
BC=EF
所以,△ABC≌△DEF(ASA)例:已知△ABC与△DEC都是等腰直角三角形,
∠ACB=∠DCE=900,D是AB上一点.
求证: △ACE≌△BCD
证明:因为△ABC与△DEC都是等腰直角三角形,且∠ACB=∠DCE=900,
所以,AC=BC,EC=DC.
∠ACB-∠3=∠DCE-∠3
即∠1=∠2
在△DBC与△AEC中
因为 BC=AC
∠1=∠2
BC=EC
所以, △DBC≌△AEC (ASA)
7.相似证明基本格式
在△ABC与△DEF中
因为∠A=∠D,∠B=∠E
所以,△ABC∽△DEF平行不能直接得相似例:已知AB=6,DB=4,BC=5,DE∥BC,求DE的长.解题格式:因为DE∥BC,所以∠ADE=∠B,
在△ADE与△ABC中
因为∠ADE=∠B ,∠A为公共角
所以△ADE∽△ABC
所以 即┄ 例:如图,点C在⊙O上,AC=PC,PC是⊙O的切线,AB是直径,PB=3,M是下半圆上一个动点,当△ABM的面积最大时,求MN?MC的值.在△BMN与△CBM中
因为∠1=∠2,∠BMC为公共角
所以, △BMN ∽△CBM
所以,即:8.求二次函数的最值与增减性指出开口,明确最大(小)值.
当x=┄时,y的最大值是┄.
因为a┄,所以当x>┄(x<┄)时y随x增大而增大(减小).例:求二次函数 的最大或最小值.当x取何值时,y随x增大而减小?解:因为
所以,函数有最小值.
当 时,
y的最小值为 因为
抛物线的对称轴是
所以,当x<-3/4时, y随x增大而减小.9.求抛物线的解析式过(0,m)的抛物线要设为:
y=ax 2+bx+m例:求过点(-1,2),(2,3),(0,-4)的抛物线的解析式.解:因为所求的抛物线过点(0,-4),
所以设它的解析式为y=ax2 + bx-4
又因为该抛物线过点(-1,2),(2,3)
所以┄10.一次和二次函数增减性应用“因为k>0,所以y随x的增大而增大”
“因为a>0,所以当x>m时,y随x的增大而增大”
例:A、B两市分别有某种库存机器12台和6台,现决定支援C村10台、D村8台。已知从A市调运一台到C和D村的运费分别是400元和800元,从B调运一台支C和D村的运费分别是300元和500元.
(1)设B运往C的机器x台,求总运费y关于x的函数;
(2)求出总运费最低的调运方案,并求最低运费.解: (1)由已知┄
所以y=200x+8600(0≤x≤6的非负整数)
(2)因为y=200x+8600是一次函数,
且k=200>0,所以y随x的增大而增大,
所以当x取最小值时y值最小,即x=0时y的最小值为200╳0+8600=8600
答:┄11.作图题要答题O结论:⊙O即为所求12.条件探索题要以探索所得的结果为条件证明问题成立.例:把两个全等的等腰直角△ABC和△EFG(直角边长都为4)如图放置,且使三角板EFG的顶点与ABC的斜边中点重合,绕O旋转EFG(旋转角在0到90度之间).
(1)连接HK,设BH=X,GKH的面积为Y,求Y与X的函数关系;
(2)在(1)中是否存在X,使△GKH的面积恰好等于△ABC面积的5/16?若存在,求出此时的X值,若不存在,说明理由.(2)答:当X=1或X=3时,△GKH的面积恰好等于△ABC面积的5/16.
证明:当X=1时,
当X=3时,xy
例:计算2.解不等式组解题步骤;数轴表示
例:解不等式组,并用数轴表示解集解:解① 得
解② 得①②所以不等式组的解集为在数轴上表示解集为3.解方程分式方程:去分母不漏乘,去括号注意负号;要注意验根格式.
例:解分式方程解:分式两边同乘以得,解得,经检验何知 是方程的根 所以原方程的根是解二次方程(用因式分解法)解:原方程整理为即所以原方程的根为解二次方程(配方法)解:原方程整理为配方得原方程的根为所以即 或 解二次方程(公式法)解:原方程整理为因为原方程的根为所以4.统计问题树形图画法,等可能事件计算,概率表示.
例:口袋里装有2个白球1个红球1个黑球,它们的大小相同.现从中任取两个球,用树形图表示摸出两个白球的各种形况,并求它的概率.解:画树形图由图可知,等可能事件共有12种,其中两个球都是白球的事件有2种.所以摸出两个白球的概率是或P(摸出两个白球)=5.圆的切线证明半径+垂直=切线(判定定理)
例:如图,A,B是⊙O上的点,MN是过A点的直线,若∠AOB=2∠BAM.求证:MN切⊙O于点A.半径+垂直=切线(判定定理)
证明: 因为A,B是⊙O上的点,所以OA=OB,
所以,∠1=∠B,
在△ABO中,因为∠1+∠B+∠AOB=1800,
即,∠AOB=1800- 2∠1,
又因,∠AOB=2∠BAM
所以,1800-2∠1=2∠BAM
2∠BAM +2∠1=1800
∠BAM +∠1=900
即,OA⊥MN于A点,
又因OA是⊙O的半径
所以,MN切⊙O于点A6.证明三角形全等基本格式
在△ABC与△DEF中
因为 AB=DE
∠B=∠E
BC=EF
所以,△ABC≌△DEF(ASA)例:已知△ABC与△DEC都是等腰直角三角形,
∠ACB=∠DCE=900,D是AB上一点.
求证: △ACE≌△BCD
证明:因为△ABC与△DEC都是等腰直角三角形,且∠ACB=∠DCE=900,
所以,AC=BC,EC=DC.
∠ACB-∠3=∠DCE-∠3
即∠1=∠2
在△DBC与△AEC中
因为 BC=AC
∠1=∠2
BC=EC
所以, △DBC≌△AEC (ASA)
7.相似证明基本格式
在△ABC与△DEF中
因为∠A=∠D,∠B=∠E
所以,△ABC∽△DEF平行不能直接得相似例:已知AB=6,DB=4,BC=5,DE∥BC,求DE的长.解题格式:因为DE∥BC,所以∠ADE=∠B,
在△ADE与△ABC中
因为∠ADE=∠B ,∠A为公共角
所以△ADE∽△ABC
所以 即┄ 例:如图,点C在⊙O上,AC=PC,PC是⊙O的切线,AB是直径,PB=3,M是下半圆上一个动点,当△ABM的面积最大时,求MN?MC的值.在△BMN与△CBM中
因为∠1=∠2,∠BMC为公共角
所以, △BMN ∽△CBM
所以,即:8.求二次函数的最值与增减性指出开口,明确最大(小)值.
当x=┄时,y的最大值是┄.
因为a┄,所以当x>┄(x<┄)时y随x增大而增大(减小).例:求二次函数 的最大或最小值.当x取何值时,y随x增大而减小?解:因为
所以,函数有最小值.
当 时,
y的最小值为 因为
抛物线的对称轴是
所以,当x<-3/4时, y随x增大而减小.9.求抛物线的解析式过(0,m)的抛物线要设为:
y=ax 2+bx+m例:求过点(-1,2),(2,3),(0,-4)的抛物线的解析式.解:因为所求的抛物线过点(0,-4),
所以设它的解析式为y=ax2 + bx-4
又因为该抛物线过点(-1,2),(2,3)
所以┄10.一次和二次函数增减性应用“因为k>0,所以y随x的增大而增大”
“因为a>0,所以当x>m时,y随x的增大而增大”
例:A、B两市分别有某种库存机器12台和6台,现决定支援C村10台、D村8台。已知从A市调运一台到C和D村的运费分别是400元和800元,从B调运一台支C和D村的运费分别是300元和500元.
(1)设B运往C的机器x台,求总运费y关于x的函数;
(2)求出总运费最低的调运方案,并求最低运费.解: (1)由已知┄
所以y=200x+8600(0≤x≤6的非负整数)
(2)因为y=200x+8600是一次函数,
且k=200>0,所以y随x的增大而增大,
所以当x取最小值时y值最小,即x=0时y的最小值为200╳0+8600=8600
答:┄11.作图题要答题O结论:⊙O即为所求12.条件探索题要以探索所得的结果为条件证明问题成立.例:把两个全等的等腰直角△ABC和△EFG(直角边长都为4)如图放置,且使三角板EFG的顶点与ABC的斜边中点重合,绕O旋转EFG(旋转角在0到90度之间).
(1)连接HK,设BH=X,GKH的面积为Y,求Y与X的函数关系;
(2)在(1)中是否存在X,使△GKH的面积恰好等于△ABC面积的5/16?若存在,求出此时的X值,若不存在,说明理由.(2)答:当X=1或X=3时,△GKH的面积恰好等于△ABC面积的5/16.
证明:当X=1时,
当X=3时,xy
同课章节目录
