8.1.2样本相关系数课件(共31张PPT)
文档属性
| 名称 | 8.1.2样本相关系数课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 21:35:44 | ||
图片预览








文档简介
(共31张PPT)
8.1.2样本相关系数
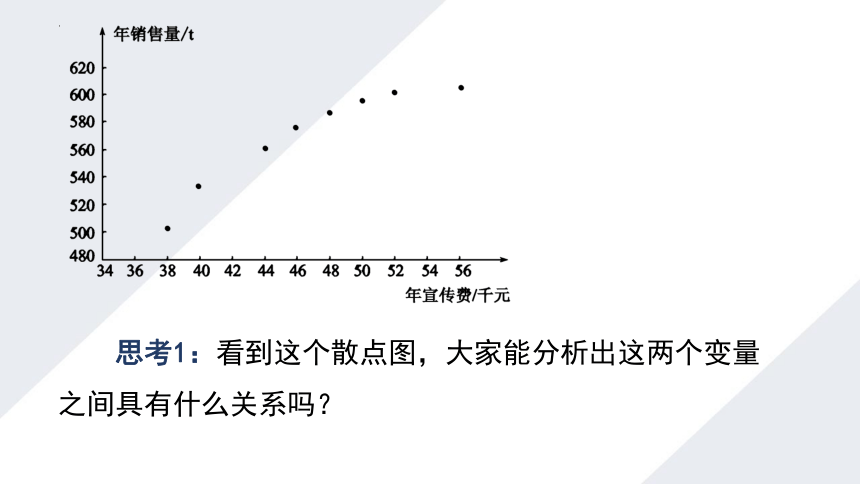
思考1:看到这个散点图,大家能分析出这两个变量之间具有什么关系吗?
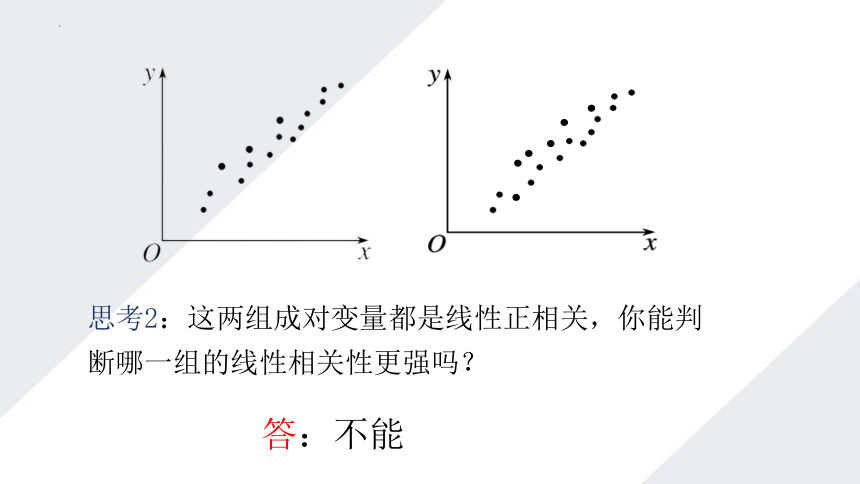
思考2:这两组成对变量都是线性正相关,你能判断哪一组的线性相关性更强吗?
答:不能
通过观察散点图中成对样本数据的分布规律,我们可以大致推断两个变量是否存在相关关系、是正相关还是负相关、是线性相关还是非线性相关等.
散点图虽然直观,但无法确切地反映成对样本数据的相关程度,也就无法量化两个变量之间相关程度的大小. 能否像引入均值、方差等数字特征对单个变量数据进行分析那样,引入一个适当的“数字特征”,对成对样本数据的相关程度进行定量分析呢
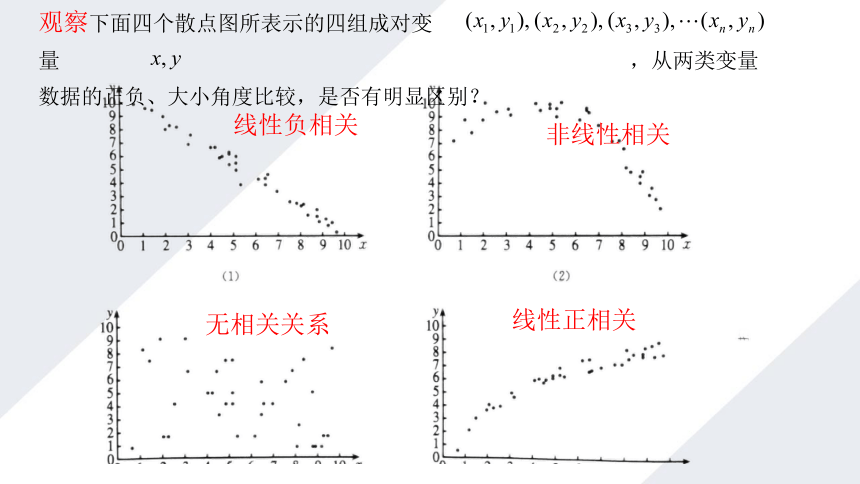
线性负相关
线性正相关
无相关关系
非线性相关
观察下面四个散点图所表示的四组成对变量 ,从两类变量 数据的正负、大小角度比较,是否有明显区别?
对于变量x和变量y,设经过随机抽样获得的成对样本数据为(x1, y1), (x2, y2), , (xn, yn),其中x1, x2, , xn和y1, y2, , yn的均值分别为 和 . 将数据以 为零点进行平移,得到平移后的成对数据为
并绘制散点图.
数据预处理的常用方法:中心化(零均值化)
线性负相关
线性正相关
无相关关系
非线性相关
(x,y)基本异号
(x,y)基本同号
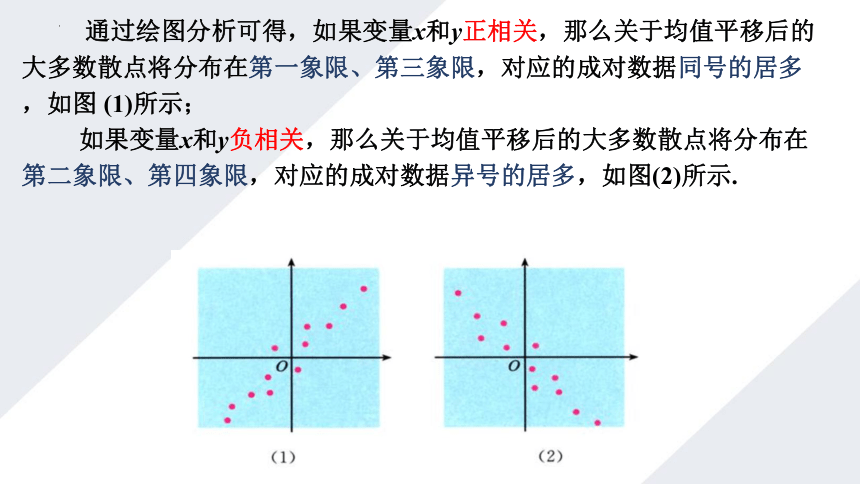
通过绘图分析可得,如果变量x和y正相关,那么关于均值平移后的大多数散点将分布在第一象限、第三象限,对应的成对数据同号的居多,如图 (1)所示;
如果变量x和y负相关,那么关于均值平移后的大多数散点将分布在第二象限、第四象限,对应的成对数据异号的居多,如图(2)所示.
根据上述分析,你能利用正相关变量和负相关变量的成对样本数据平移后呈现的规律,构造一个度量成对样本数据是正相关还是负相关的数字特征吗
利用散点 的横、纵坐标是否同号,可以构造一个量
一般情形下,Lxy>0表明成对样本数据正相关;Lxy <0表明成对样本数据负相关.
在研究体重与身高之间的相关程度时,如果体重的单位不变,把身高单位由米改为厘米,单位的改变不会改变体重与身高之间的相关程度.
变换单位前
变换单位后
变换单位后是变换前的100倍
我们发现, Lxy的大小与数据的度量单位有关,所以不能直接用它度量成对样本数据相关程度的大小.
因为Lxy的大小与数据的度量单位有关,所以不宜直接用它度量成对样本数据相关程度的大小. 为了消除度量单位的影响,需要对数据作进一步的“标准化”处理. 我们用
我们称r为变量x和变量y的样本线性相关系数,
简称样本相关系数.
当r>0时,称成对样本数据正相关;当其中一个数据的值变小时,另一个数据的值通常也变小;当其中一个数据的值变大时,另一个数据的值通常也变大。
当r<0时,称成对样本数据负相关;当其中一个数据的值变小时,另一个数据的值通常会变大:当其中一个数据的值变大时,另一个数据的值通常会变小。
样本相关系数r的正负能反映出成对变量的什么关系?
样本相关系数r是一个描述成对样本数据的数字特征,它反映了两个随机变量之间的线性相关程度.
r的符号反映了相关关系的正负性.
|r|的大小反映了两个变量线性相关的程度,即散点集中于一条直线的程度.
① |r|≤1;
② 当|r|越接近1时,成对数据的线性相关程度越强; 当|r|越接近0时,成对数据的线性相关程度越弱;特别地,当|r|=0时,成对数据的没有线性相关关系;当|r|=1时,成对数据都落在一条直线上.
样本相关系数r=0时,样本一定是无相关关系吗?
r=0时,只表明成对样本数据间没有线性相关关系,但不排除它们之间有其他相关关系.
答:
补充:利用相关系数r来检验线性相关显著性水平时,通常与0.75作比较.
若0.75≤|r|≤1,则认为y与x的线性相关程度很强;
若0.3≤|r|<0.75,则认为y与x的线性相关程度一般;
若|r|≤0.25,则认为y与x的线性相关程度较弱
图(1) 中成对样本数据的正线性相关程度很强.
图(2) 中成对样本数据的负线性相关程度比较强.
图(3)中 对样本数据的线性相关程度很弱.
图(4)中成对样本数据的线性相关程度极弱.
练习:两个变量之间的相关程度越低,则其线性相关系数的数值( )
A.越小 B. 越接近1 C. 越接近0 D.越接近-1
练习:给定y与x是一组样本数据,求得样本相关系数r=-0.730,则( )
A.y与x线性不相关 B.y与x 正线性相关
C.y与x负线性相关 D.以上都不对
例1:根据下表中脂肪含量和年龄的样本数据,画出散点图,判断成对样本数据是否线性相关,并通过样本相关系数判断年龄和脂肪的相关程度和变化趋势的异同?
参考数据:
解:先画出散点图,如下图所示:
观察散点图,可以看出样本点都集中在一条直线附近,由此推断脂肪含量和年龄线性相关。
参考数据:
由样本相关系数 ,可以推断脂肪含量和年龄这两个变量正线性相关,且相关程度很强。脂肪含量与年龄变化趋势相同。
课本P103 练习 2
已知变量x和变量y的3对随机观测数据(2, 2), (3, -1), (5, -7),计算成对样本数据的样本相关系数. 能据此推断这两个变量线性相关吗 为什么
已知变量x和变量y的3对随机观测数据(2, 2), (3, -1), (5, -7),计算成对样本数据的样本相关系数. 能据此推断这两个变量线性相关吗 为什么
解:
由样本数据可得
虽然样本相关系数为-1,三个样本点在一条直线上,但是由于样本量太小,据此推断两个变量完全线性相关并不可靠.
练习:假设关于某种设备的使用年限x(年)与所支出的维修费用 y(万元)有如下统计资料∶
已知,,,
(1)求,;
(2)对x,y进行线性相关性检验.
x 2 3 4 5 6
y 2.2 3.8 5.5 6.5 7.0
例2 有人收集了某城市居民年收入(所有居民在一年内收人的总和)与A商品销售额的10年数据,如下表所示.
解:
第n年 1 2 3 4 5 6 7 8 9 10
居民年收入/亿元 32.2 31.1 32.9 35.8 37.1 38.0 39.0 43.0 44.6 46.0
A商品销售额/万元 25.0 30.0 34.0 37.0 39.0 41.0 42.0 44.0 48.0 51.0
画出散点图,推断成对样本数据是否线性相关,并通过样本相关系数推断居民年收入与A商品销售额的相关程度和变化趋势的异同.
解:
画出成对样本数据的散点图,如图所示.从散点图看,A商品销售额与居民年收人的样本数据呈现出线性相关关系.
由样本数据计算得样本相关系数r≈0.95. 由此可以推断,A商品销售额与居民年收入正线性相关,即A商品销售额与居民年收入有相同的变化趋势,且相关程度很强.
例3 在某校高一年级 中随机抽取25名男生,测得他们的身高、体重、臂展等数据,如下表所示.
体重与身高、臂展与身高分别具有怎样的相关性
编号 身高/cm 体重/kg 臂展/cm 编号 身高/cm 体重/kg 臂展/cm
1 2 3 4 5 6 7 8 9 10 11 12 13 173 179 175 179 182 173 180 170 169 1 77 177 178 174 55 71 52 62 82 63 55 81 54 54 59 67 56 169 170 172 177 174 166 174 1 69 1 66 176 170 174 170 14 15 16 17 18 19 20 21 22 23 24 25 166 176 176 175 169 184 169 182 171 177 173 173 66 61 49 60 48 86 58 54 58 61 58 51 161
166
165
173
162
189
164
170
164
173
165
169
根据样本数据画出体重与身高、臂展与身高的散点图,分别如图 (1)和(2)所示,两个散点图都呈现出线性相关的特征.
解:
通过计算得到体重与身高、臂展与身高的样本相关系数分别约为0.34和0.78,都为正线性相关. 其中,臂展与身高的相关程度更高.
小结:
1. 样本相关系数:
2.相关系数的性质:
① 当r>0时,称成对样本数据正相关;当r<0时,称成对样本数据负相关.
② |r|≤1;
③ 当|r|越接近1时,成对数据的线性相关程度越强;当|r|越接近0时,成对数据的线性相关程度越弱;特别地,当|r|=0时,成对数据的没有线性相关关系;当|r|=1时,成对数据都落在一条直线上.
本小节结束
8.1.2样本相关系数
思考1:看到这个散点图,大家能分析出这两个变量之间具有什么关系吗?
思考2:这两组成对变量都是线性正相关,你能判断哪一组的线性相关性更强吗?
答:不能
通过观察散点图中成对样本数据的分布规律,我们可以大致推断两个变量是否存在相关关系、是正相关还是负相关、是线性相关还是非线性相关等.
散点图虽然直观,但无法确切地反映成对样本数据的相关程度,也就无法量化两个变量之间相关程度的大小. 能否像引入均值、方差等数字特征对单个变量数据进行分析那样,引入一个适当的“数字特征”,对成对样本数据的相关程度进行定量分析呢
线性负相关
线性正相关
无相关关系
非线性相关
观察下面四个散点图所表示的四组成对变量 ,从两类变量 数据的正负、大小角度比较,是否有明显区别?
对于变量x和变量y,设经过随机抽样获得的成对样本数据为(x1, y1), (x2, y2), , (xn, yn),其中x1, x2, , xn和y1, y2, , yn的均值分别为 和 . 将数据以 为零点进行平移,得到平移后的成对数据为
并绘制散点图.
数据预处理的常用方法:中心化(零均值化)
线性负相关
线性正相关
无相关关系
非线性相关
(x,y)基本异号
(x,y)基本同号
通过绘图分析可得,如果变量x和y正相关,那么关于均值平移后的大多数散点将分布在第一象限、第三象限,对应的成对数据同号的居多,如图 (1)所示;
如果变量x和y负相关,那么关于均值平移后的大多数散点将分布在第二象限、第四象限,对应的成对数据异号的居多,如图(2)所示.
根据上述分析,你能利用正相关变量和负相关变量的成对样本数据平移后呈现的规律,构造一个度量成对样本数据是正相关还是负相关的数字特征吗
利用散点 的横、纵坐标是否同号,可以构造一个量
一般情形下,Lxy>0表明成对样本数据正相关;Lxy <0表明成对样本数据负相关.
在研究体重与身高之间的相关程度时,如果体重的单位不变,把身高单位由米改为厘米,单位的改变不会改变体重与身高之间的相关程度.
变换单位前
变换单位后
变换单位后是变换前的100倍
我们发现, Lxy的大小与数据的度量单位有关,所以不能直接用它度量成对样本数据相关程度的大小.
因为Lxy的大小与数据的度量单位有关,所以不宜直接用它度量成对样本数据相关程度的大小. 为了消除度量单位的影响,需要对数据作进一步的“标准化”处理. 我们用
我们称r为变量x和变量y的样本线性相关系数,
简称样本相关系数.
当r>0时,称成对样本数据正相关;当其中一个数据的值变小时,另一个数据的值通常也变小;当其中一个数据的值变大时,另一个数据的值通常也变大。
当r<0时,称成对样本数据负相关;当其中一个数据的值变小时,另一个数据的值通常会变大:当其中一个数据的值变大时,另一个数据的值通常会变小。
样本相关系数r的正负能反映出成对变量的什么关系?
样本相关系数r是一个描述成对样本数据的数字特征,它反映了两个随机变量之间的线性相关程度.
r的符号反映了相关关系的正负性.
|r|的大小反映了两个变量线性相关的程度,即散点集中于一条直线的程度.
① |r|≤1;
② 当|r|越接近1时,成对数据的线性相关程度越强; 当|r|越接近0时,成对数据的线性相关程度越弱;特别地,当|r|=0时,成对数据的没有线性相关关系;当|r|=1时,成对数据都落在一条直线上.
样本相关系数r=0时,样本一定是无相关关系吗?
r=0时,只表明成对样本数据间没有线性相关关系,但不排除它们之间有其他相关关系.
答:
补充:利用相关系数r来检验线性相关显著性水平时,通常与0.75作比较.
若0.75≤|r|≤1,则认为y与x的线性相关程度很强;
若0.3≤|r|<0.75,则认为y与x的线性相关程度一般;
若|r|≤0.25,则认为y与x的线性相关程度较弱
图(1) 中成对样本数据的正线性相关程度很强.
图(2) 中成对样本数据的负线性相关程度比较强.
图(3)中 对样本数据的线性相关程度很弱.
图(4)中成对样本数据的线性相关程度极弱.
练习:两个变量之间的相关程度越低,则其线性相关系数的数值( )
A.越小 B. 越接近1 C. 越接近0 D.越接近-1
练习:给定y与x是一组样本数据,求得样本相关系数r=-0.730,则( )
A.y与x线性不相关 B.y与x 正线性相关
C.y与x负线性相关 D.以上都不对
例1:根据下表中脂肪含量和年龄的样本数据,画出散点图,判断成对样本数据是否线性相关,并通过样本相关系数判断年龄和脂肪的相关程度和变化趋势的异同?
参考数据:
解:先画出散点图,如下图所示:
观察散点图,可以看出样本点都集中在一条直线附近,由此推断脂肪含量和年龄线性相关。
参考数据:
由样本相关系数 ,可以推断脂肪含量和年龄这两个变量正线性相关,且相关程度很强。脂肪含量与年龄变化趋势相同。
课本P103 练习 2
已知变量x和变量y的3对随机观测数据(2, 2), (3, -1), (5, -7),计算成对样本数据的样本相关系数. 能据此推断这两个变量线性相关吗 为什么
已知变量x和变量y的3对随机观测数据(2, 2), (3, -1), (5, -7),计算成对样本数据的样本相关系数. 能据此推断这两个变量线性相关吗 为什么
解:
由样本数据可得
虽然样本相关系数为-1,三个样本点在一条直线上,但是由于样本量太小,据此推断两个变量完全线性相关并不可靠.
练习:假设关于某种设备的使用年限x(年)与所支出的维修费用 y(万元)有如下统计资料∶
已知,,,
(1)求,;
(2)对x,y进行线性相关性检验.
x 2 3 4 5 6
y 2.2 3.8 5.5 6.5 7.0
例2 有人收集了某城市居民年收入(所有居民在一年内收人的总和)与A商品销售额的10年数据,如下表所示.
解:
第n年 1 2 3 4 5 6 7 8 9 10
居民年收入/亿元 32.2 31.1 32.9 35.8 37.1 38.0 39.0 43.0 44.6 46.0
A商品销售额/万元 25.0 30.0 34.0 37.0 39.0 41.0 42.0 44.0 48.0 51.0
画出散点图,推断成对样本数据是否线性相关,并通过样本相关系数推断居民年收入与A商品销售额的相关程度和变化趋势的异同.
解:
画出成对样本数据的散点图,如图所示.从散点图看,A商品销售额与居民年收人的样本数据呈现出线性相关关系.
由样本数据计算得样本相关系数r≈0.95. 由此可以推断,A商品销售额与居民年收入正线性相关,即A商品销售额与居民年收入有相同的变化趋势,且相关程度很强.
例3 在某校高一年级 中随机抽取25名男生,测得他们的身高、体重、臂展等数据,如下表所示.
体重与身高、臂展与身高分别具有怎样的相关性
编号 身高/cm 体重/kg 臂展/cm 编号 身高/cm 体重/kg 臂展/cm
1 2 3 4 5 6 7 8 9 10 11 12 13 173 179 175 179 182 173 180 170 169 1 77 177 178 174 55 71 52 62 82 63 55 81 54 54 59 67 56 169 170 172 177 174 166 174 1 69 1 66 176 170 174 170 14 15 16 17 18 19 20 21 22 23 24 25 166 176 176 175 169 184 169 182 171 177 173 173 66 61 49 60 48 86 58 54 58 61 58 51 161
166
165
173
162
189
164
170
164
173
165
169
根据样本数据画出体重与身高、臂展与身高的散点图,分别如图 (1)和(2)所示,两个散点图都呈现出线性相关的特征.
解:
通过计算得到体重与身高、臂展与身高的样本相关系数分别约为0.34和0.78,都为正线性相关. 其中,臂展与身高的相关程度更高.
小结:
1. 样本相关系数:
2.相关系数的性质:
① 当r>0时,称成对样本数据正相关;当r<0时,称成对样本数据负相关.
② |r|≤1;
③ 当|r|越接近1时,成对数据的线性相关程度越强;当|r|越接近0时,成对数据的线性相关程度越弱;特别地,当|r|=0时,成对数据的没有线性相关关系;当|r|=1时,成对数据都落在一条直线上.
本小节结束
