从分数到分式
图片预览











文档简介
课件39张PPT。 丝茅草两边有许多小细齿,能轻易地把人的手指划出一道血口子,非常锋利. 新课导入 如果将铁片的边上也刻成许多小细齿,自然会更加锋利,可以用来更快地伐倒大树了. 鲁班根据丝茅草叶的细齿,请铁匠仿制出世界上第一根锯条. ——鲁班就是这样根据类比的道理发明了锯子. 在数学中,应用类比推理的地方有很多. 所谓类比,就是由两个对象的某些相同或相似的性质,推断它们在其他性质上也有可能相同或相似的一种推理形式. 【知识与能力】
了解分式产生的背景和分式的概念;
了解分式与整式概念的区别与联系, 培养学生分析、归纳、概括的能力;
掌握分式有意义的条件,认识事物间的联系与制约关系,培养逆向思维能力和辩证唯物主义观点. 教学目标 【过程与方法】
用字母表示现实生活中的数量关系,体会分式的模型思想;
能从具体情境中抽象出数量关系和变化规律,经历对具体问题的探索过程,进一步培养符号感;
培养认识特殊与一般的辩证关系. 【情感态度与价值观】
通过丰富的现实情境,在已有数学经验的基础上,了解数学的价值,发展“用数学”的信心;
在现实情境中进一步理解用字母表示数的意义,发展符号感;
体会合作交流,小组讨论的优越性. 1. 了解分式的形式 (A、B是整式);
2. 理解分式概念中的一个特点:分母中含有字母;
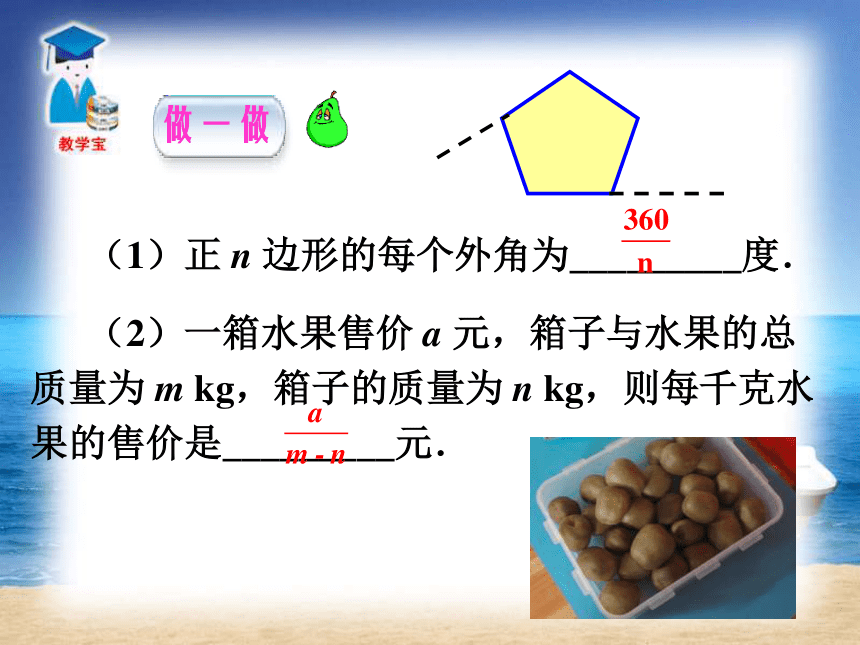
3. 一个要求:分母的取值限于使分母的值不得为零.重点理解和掌握分式有意义的条件.难点 教学重难点 那么,小红 x 分钟折了50 只,每分钟折多少个呢?怎样用式子表示? 手工课上,小红 10 分钟折了5 只大公鸡,每分钟折多少个?怎样用式子表示? 分数怎样给它命名?? (1)正 n 边形的每个外角为_________度.
(2)一箱水果售价 a 元,箱子与水果的总质量为 m kg,箱子的质量为 n kg,则每千克水果的售价是_________元.做一做 (3)有两片枣树,一片 x 公顷,收枣 m 千克,另一片 y 公顷,收枣 n 千克,这两片枣树平均每公顷的产量是_________千克.
(4)△ABC 的面积为 S ,BC 边长为 a ,高 AD 为_________. (5)长方形的面积为10 cm2,长为7 cm,宽应为________cm;
长方形的面积为S,长为 a ,宽应为________ cm . (6)把体积为 200 cm3的水倒入底面积为 33 cm2 的圆柱形容器中,水面高度为____ cm;
把体积为 V 的水倒入
底面积为 S 的圆柱形容器
中,水面高度为_______ . 这些式子有什么共同点? 它们与分数有什么联系与区别?你能总结出什么规律?都具有分数的形式分母中有字母分子分母中全是数字想一想分子分母=A×必须含有字母.分式是不同于整式的另一类式子. 分式整式整式分式有理式单项式多项式…………分式比分数更具有一般性.……分数分式…… 从“ 2、-3、a、-m、2x + 3y ”中任选数字或字母,组成一个分式. 拼式游戏 在分式的概念中,隐含了一个条件,你知道吗? 分式中,分母可以取任意实数吗? 在分数中,分母不能为0 !提示想一想分式的分母也不能为0!结论:B ≠ 0B = 0B ≠ 0B = 0A = 0A≠0分式无意义.分式有意义.分式有意义.分式无意义.尊重分母!
母之不存,子有何义?
分子可正可负可零.解:当分母 4 x+1 ≠ 0 ,
即 x≠【例1】? 当 x 取何值时,下列分式有意义?(1)解:当分母 x-3 ≠ 0 ,
即 x≠3 时,原分式有意义.(2)时,原分式有意义.解:当分母 2|x|-3 ≠ 0 ,
即 x≠(3)解:∵分母( x2 + 1)>0 恒成立,
∴ x 取任意实数时,原分式都有意义.(4)时,原分式有意义. 分式的分子、分母有公因式 x+2 ,若先将公因式约去 ,此时分母的字母取值范围为 x≠2,扩大了分母的范围,所以不能先约去公因式!(5)解:当 x2 - 4 ≠ 0 ,
即 x ≠ ±2 时,原分式有意义.错误解法解:
当 x - 2 ≠ 0 ,
即 x ≠ 2 时,原分式有意义.×√正确解法【例2】当 x 取何值时,下列分式无意义? 解:当分母 x -1 = 0 ,
即 x = 1 时,原分式无意义.(1)解:当分母 3x = 0 ,
即 x = 0 时,原分式无意义.(2) 【例3】当 x 取何值时,下列分式的值为零?(1)解:当分子 x + 3 = 0 得 x =-3 .
且当 x =-3时,分母 2x-5 =-6-5≠0 .
∴当x =-3时,原分式的值为零.(2)解:当分子|x|- 2 = 0 得 x = ±2 .
而当x = 2 时,分母 x2 + x - 6 = 4 + 2 - 6 = 0 ,
原分式无意义.
但当x =-2时,分母 x2 + x - 6 = 4 – 2 – 6≠0 ,
∴当x =-2时,原分式的值为零.(3)解:当分子3-|x|= 0 得 x = ±3.
而当x = 3时,分母 x2-3x + 3 = 9-9+3≠0 ,
当x = -3时,分母 x2-3x + 3=9-3× (-3)+3≠0
∴当 x = 3 或 x = -3 时,原分式的值都为零.1.分式的基本概念:有理式整式分式 课堂小结 只有满足了分式的分母不能为 0 这个条件,分式才有意义.即当B≠0时,分式 才有意义.2.分式何时有意义: 必须在分式有意义的前提下考虑,既要考虑使分子取值为 0 ,又要考虑不使分母为 0 ,二者缺一不可!3.分式的值何时为零?即当 A = 0 且B≠0时,分式 才有意义.1. 你能构造出多少个分式? 随堂练习 2. 当 m 为何值时,下列分式的值为0? m = 0m = 2m = 1 3. 当 x 取何值时,下列分式有意义? x ≠-2x ≠x ≠±2 4. 当 x 为任意实数时,下列分式一定有意义的是( )B 5. 甲﹑乙二人从 A 地走到 B 地,甲每时走 a 千米,乙每时走 b 千米,a>b.如果乙提前 1 小时出发,那么甲追上乙需要多长时间?当a=6,b=5时,求甲追上乙所需的时间?(1)乙先行 1 小时走的路程是 1×b(千米), AB 甲比乙每小时多走(a-b)千米,所以甲追上乙所需的时间是:b÷(a-b)=解: 答:甲追上乙需要 时.当a=6,b=5 时,甲追上乙需要 5 小时.(2)当a=6,b=5 时,甲追上乙所需的时间是: 4. 根据实例编写一个分式,并说出它何时有意义,自己给出一个适当的值,求出分式的值.
了解分式产生的背景和分式的概念;
了解分式与整式概念的区别与联系, 培养学生分析、归纳、概括的能力;
掌握分式有意义的条件,认识事物间的联系与制约关系,培养逆向思维能力和辩证唯物主义观点. 教学目标 【过程与方法】
用字母表示现实生活中的数量关系,体会分式的模型思想;
能从具体情境中抽象出数量关系和变化规律,经历对具体问题的探索过程,进一步培养符号感;
培养认识特殊与一般的辩证关系. 【情感态度与价值观】
通过丰富的现实情境,在已有数学经验的基础上,了解数学的价值,发展“用数学”的信心;
在现实情境中进一步理解用字母表示数的意义,发展符号感;
体会合作交流,小组讨论的优越性. 1. 了解分式的形式 (A、B是整式);
2. 理解分式概念中的一个特点:分母中含有字母;
3. 一个要求:分母的取值限于使分母的值不得为零.重点理解和掌握分式有意义的条件.难点 教学重难点 那么,小红 x 分钟折了50 只,每分钟折多少个呢?怎样用式子表示? 手工课上,小红 10 分钟折了5 只大公鸡,每分钟折多少个?怎样用式子表示? 分数怎样给它命名?? (1)正 n 边形的每个外角为_________度.
(2)一箱水果售价 a 元,箱子与水果的总质量为 m kg,箱子的质量为 n kg,则每千克水果的售价是_________元.做一做 (3)有两片枣树,一片 x 公顷,收枣 m 千克,另一片 y 公顷,收枣 n 千克,这两片枣树平均每公顷的产量是_________千克.
(4)△ABC 的面积为 S ,BC 边长为 a ,高 AD 为_________. (5)长方形的面积为10 cm2,长为7 cm,宽应为________cm;
长方形的面积为S,长为 a ,宽应为________ cm . (6)把体积为 200 cm3的水倒入底面积为 33 cm2 的圆柱形容器中,水面高度为____ cm;
把体积为 V 的水倒入
底面积为 S 的圆柱形容器
中,水面高度为_______ . 这些式子有什么共同点? 它们与分数有什么联系与区别?你能总结出什么规律?都具有分数的形式分母中有字母分子分母中全是数字想一想分子分母=A×必须含有字母.分式是不同于整式的另一类式子. 分式整式整式分式有理式单项式多项式…………分式比分数更具有一般性.……分数分式…… 从“ 2、-3、a、-m、2x + 3y ”中任选数字或字母,组成一个分式. 拼式游戏 在分式的概念中,隐含了一个条件,你知道吗? 分式中,分母可以取任意实数吗? 在分数中,分母不能为0 !提示想一想分式的分母也不能为0!结论:B ≠ 0B = 0B ≠ 0B = 0A = 0A≠0分式无意义.分式有意义.分式有意义.分式无意义.尊重分母!
母之不存,子有何义?
分子可正可负可零.解:当分母 4 x+1 ≠ 0 ,
即 x≠【例1】? 当 x 取何值时,下列分式有意义?(1)解:当分母 x-3 ≠ 0 ,
即 x≠3 时,原分式有意义.(2)时,原分式有意义.解:当分母 2|x|-3 ≠ 0 ,
即 x≠(3)解:∵分母( x2 + 1)>0 恒成立,
∴ x 取任意实数时,原分式都有意义.(4)时,原分式有意义. 分式的分子、分母有公因式 x+2 ,若先将公因式约去 ,此时分母的字母取值范围为 x≠2,扩大了分母的范围,所以不能先约去公因式!(5)解:当 x2 - 4 ≠ 0 ,
即 x ≠ ±2 时,原分式有意义.错误解法解:
当 x - 2 ≠ 0 ,
即 x ≠ 2 时,原分式有意义.×√正确解法【例2】当 x 取何值时,下列分式无意义? 解:当分母 x -1 = 0 ,
即 x = 1 时,原分式无意义.(1)解:当分母 3x = 0 ,
即 x = 0 时,原分式无意义.(2) 【例3】当 x 取何值时,下列分式的值为零?(1)解:当分子 x + 3 = 0 得 x =-3 .
且当 x =-3时,分母 2x-5 =-6-5≠0 .
∴当x =-3时,原分式的值为零.(2)解:当分子|x|- 2 = 0 得 x = ±2 .
而当x = 2 时,分母 x2 + x - 6 = 4 + 2 - 6 = 0 ,
原分式无意义.
但当x =-2时,分母 x2 + x - 6 = 4 – 2 – 6≠0 ,
∴当x =-2时,原分式的值为零.(3)解:当分子3-|x|= 0 得 x = ±3.
而当x = 3时,分母 x2-3x + 3 = 9-9+3≠0 ,
当x = -3时,分母 x2-3x + 3=9-3× (-3)+3≠0
∴当 x = 3 或 x = -3 时,原分式的值都为零.1.分式的基本概念:有理式整式分式 课堂小结 只有满足了分式的分母不能为 0 这个条件,分式才有意义.即当B≠0时,分式 才有意义.2.分式何时有意义: 必须在分式有意义的前提下考虑,既要考虑使分子取值为 0 ,又要考虑不使分母为 0 ,二者缺一不可!3.分式的值何时为零?即当 A = 0 且B≠0时,分式 才有意义.1. 你能构造出多少个分式? 随堂练习 2. 当 m 为何值时,下列分式的值为0? m = 0m = 2m = 1 3. 当 x 取何值时,下列分式有意义? x ≠-2x ≠x ≠±2 4. 当 x 为任意实数时,下列分式一定有意义的是( )B 5. 甲﹑乙二人从 A 地走到 B 地,甲每时走 a 千米,乙每时走 b 千米,a>b.如果乙提前 1 小时出发,那么甲追上乙需要多长时间?当a=6,b=5时,求甲追上乙所需的时间?(1)乙先行 1 小时走的路程是 1×b(千米), AB 甲比乙每小时多走(a-b)千米,所以甲追上乙所需的时间是:b÷(a-b)=解: 答:甲追上乙需要 时.当a=6,b=5 时,甲追上乙需要 5 小时.(2)当a=6,b=5 时,甲追上乙所需的时间是: 4. 根据实例编写一个分式,并说出它何时有意义,自己给出一个适当的值,求出分式的值.
