物理人教版(2019)必修第二册第5章《抛体运动》复习(共28张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册第5章《抛体运动》复习(共28张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 680.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-26 19:52:29 | ||
图片预览








文档简介
(共28张PPT)
高一物理必修二第5章《抛体运动》
复习课件
一、曲线运动的速度方向
1.质点在某一点的速度方向,沿曲线在这一点的 ;
2.在曲线运动中速度的 是变化的,所以曲线运动是 运动.
二、物体做曲线运动的条件
1.动力学角度:当物体所受合力的方向与它的速度方向
时,物体做曲线运动.
2.运动学角度:物体加速度的方向与它的速度的方向
时,物体做曲线运动.
一、曲线运动
切线方向
方向
变速
不在同一直线上
不在同一直线上
1.曲线运动的速度
(1)质点在某一时刻(某一位置)速度的方向与这一时刻质点所在位置处的切线方向一致,故其速度的方向时刻改变.
(2)物体做曲线运动时,速度方向一定变化,但速度的大小不一定变化.
2.曲线运动的性质
(1)性质:速度是矢量,由于速度方向时刻在发生变化,所以曲线运动的加速度一定不为零,是变速运动.
(2)曲线运动一定是变速运动,但变速运动不一定是曲线运动,如匀变速直线运动.
物体做曲线运动的轨迹、速度方向与合力方向三者的关系?
轨迹、速度方向、合力方向三者不共线,合力指向轨迹的凹侧,轨迹夹在速度方向与合力方向之间
在光滑水平面上运动的物体,受到水平恒力F作用后,沿曲线MN运动,速度方向改变了90°,如图所示,则此过程中,物体受到的恒力可能是( )
A.F1 B.F2 C.F3 D.F4
B
二、运动的合成与分解
1.合运动与分运动
如果物体同时参与了几个运动,那么物体实际发生的运动就是 (选填“合运动”或“分运动”),同时参与的几个运动就是分运动.
2.运动的合成与分解:由分运动求合运动的过程,叫作运动的合成; 的过程,叫作运动的分解.
3.运动的合成与分解遵从 法则.
合运动
由合运动求分运动
矢量运算
4.合运动与分运动的四个特性
等时性 各分运动与合运动同时发生和结束,时间相同
等效性 各分运动的共同效果与合运动的效果相同
同体性 各分运动与合运动是同一物体的运动
独立性 各分运动之间互不相干,彼此独立,互不影响
5.运动的合成与分解
(1)运动的合成与分解是指位移、速度、加速度的合成与分解.其合成、分解遵循平行四边形定则.
(2)对速度v进行分解时,不能随意分解,应按物体的实际运动效果进行分解.
6.曲、直判断:
加速度(或合力)与速度方向
7.是否为匀变速运动的判断:
加速度(或合力)
互成角度的一个匀速直线运动和一个匀变速直线运动的合运动的轨迹向哪个方向弯曲?
轨迹在合初速度v0与合加速度a之间,且向合加速度一侧弯曲.
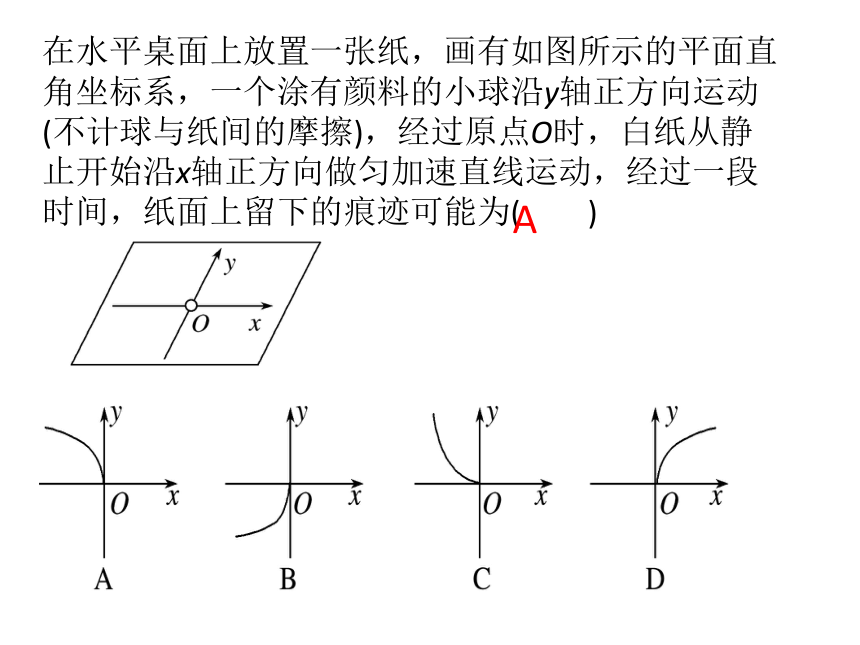
在水平桌面上放置一张纸,画有如图所示的平面直角坐标系,一个涂有颜料的小球沿y轴正方向运动(不计球与纸间的摩擦),经过原点O时,白纸从静止开始沿x轴正方向做匀加速直线运动,经过一段时间,纸面上留下的痕迹可能为( )
A
三、小船渡河问题
一条宽为d的大河,小明驾着小船从码头A出发,欲将一批货物运送到对岸的码头B.已知河水流速为v水,小船在静水中的航速为v船.
1.渡河过程中,小船参与了哪两个分运动?
2.小船如何渡河时间最短?最短时间为多少?此时渡河位移为多大?
3.小船如何渡河才能使渡河位移最小?最小位移为多大?
情况一:v水情况二:v水>v船
四、关联速度模型
1.两物体通过不可伸长的轻绳(杆)相连,当两物体都发生运动,且物体运动的方向不在绳(杆)的直线上,两物体的速度是关联的..
2.处理关联速度问题的方法:首先认清哪个是合速度、哪个是分速度.物体的实际速度一定是合速度,分解时两个分速度方向应取沿绳方向和垂直绳方向.
如图所示,岸上的小车A以速度v匀速向左运动,绳跨过光滑轻质定滑轮和小船B相连.
(1)在相等的时间内,小车A和小船B运动的位移相等吗?
(2)小车A和小船B某一时刻的速度大小相等吗?如果不相等,哪个速度大?
(3)从运动的合成和分解的角度看,小船上P点的速度可以分解为哪两个分速度?
(4)若某时刻连接船的绳与水平方向的夹角为α,则船的速度是多大?
五、实验:探究平抛运动的特点
1.抛体运动:以一定的速度将物体抛出,在空气阻力 的情况下,物体只受 作用的运动.
2.平抛运动:初速度沿 方向的抛体运动.
3.平抛运动的特点:
(1)初速度沿 方向;
(2)只受 作用.
可以忽略
重力
水平
水平
重力
方案一:频闪照相(或录制视频)的方法
以抛出点为原点,建立直角坐标系
方案二:探究平抛运动竖直分运动的特点
分别改变小球距地面的高度和小锤击打的力度,即改变A球的初速度,发现两球 ,说明平抛运动在竖直方向的分运动为 .
仍同时落地
自由落体运动.
实验:探究平抛运动水平分运动的特点
平抛运动在相等时间内水平方向位移相等,平抛运动水平方向为匀速直线运动.
六、平抛运动的规律
平抛运动的速度
水平方向:不受力,加速度是0,水平方向为匀速直线运动,vx=v0.
竖直方向:只受重力,所以a=g;竖直方向的初速度为0,所以竖直方向为自由落体运动,vy=gt.
平抛运动的速度方向沿轨迹的切线方向,速度大小、方向都不断变化.
平抛运动的位移与轨迹
1.水平位移:x=v0t
2.竖直位移:y= gt2
3.轨迹方程:y= x2,由此可知平抛运动的轨迹是一条抛物线.
平抛运动的规律
七、与斜面、曲面相结合的平抛运动
从空中水平抛出垂直落到斜面上
分解速度,构建速度三角形
vx=v0
vy=gt
从斜面水平抛出又落到斜面上
分解位移,构建位移三角形
x=v0t
y= gt2
斜面外开始,要求以最短位移打到斜面
分解位移,构建位移三角形
x=v0t
y= gt2
斜面外开始,沿斜面方向落入斜面
(与斜面距离最大)
分解速度,构建速度三角形
vx=v0
vy=gt
八、平抛运动的两个重要推论
1.做平抛运动的物体在某时刻速度方向与水平方向的夹角θ、位移方向与水平方向的夹角α的关系为tan θ=2tan α.
2.做平抛运动的物体在任意时刻的速度的反向延长线一定通过此时水平位移的中点.
如图所示,AB为半圆环ACB的水平直径,C为环上的最低点,环半径为R.一个小球从A点沿AB以速度v0抛出,不计空气阻力,则下列判断正确的是( )
A.v0越大,小球从抛出到落在半圆环上经历的时间越长
B.即使v0取值不同,小球落到环上时的速度方向和水平方向的夹角也相同
C.若v0取值适当,可以使小球垂直撞击半圆环
D.无论v0取何值,小球都不可能垂直撞击半圆环
D
再见
高一物理必修二第5章《抛体运动》
复习课件
一、曲线运动的速度方向
1.质点在某一点的速度方向,沿曲线在这一点的 ;
2.在曲线运动中速度的 是变化的,所以曲线运动是 运动.
二、物体做曲线运动的条件
1.动力学角度:当物体所受合力的方向与它的速度方向
时,物体做曲线运动.
2.运动学角度:物体加速度的方向与它的速度的方向
时,物体做曲线运动.
一、曲线运动
切线方向
方向
变速
不在同一直线上
不在同一直线上
1.曲线运动的速度
(1)质点在某一时刻(某一位置)速度的方向与这一时刻质点所在位置处的切线方向一致,故其速度的方向时刻改变.
(2)物体做曲线运动时,速度方向一定变化,但速度的大小不一定变化.
2.曲线运动的性质
(1)性质:速度是矢量,由于速度方向时刻在发生变化,所以曲线运动的加速度一定不为零,是变速运动.
(2)曲线运动一定是变速运动,但变速运动不一定是曲线运动,如匀变速直线运动.
物体做曲线运动的轨迹、速度方向与合力方向三者的关系?
轨迹、速度方向、合力方向三者不共线,合力指向轨迹的凹侧,轨迹夹在速度方向与合力方向之间
在光滑水平面上运动的物体,受到水平恒力F作用后,沿曲线MN运动,速度方向改变了90°,如图所示,则此过程中,物体受到的恒力可能是( )
A.F1 B.F2 C.F3 D.F4
B
二、运动的合成与分解
1.合运动与分运动
如果物体同时参与了几个运动,那么物体实际发生的运动就是 (选填“合运动”或“分运动”),同时参与的几个运动就是分运动.
2.运动的合成与分解:由分运动求合运动的过程,叫作运动的合成; 的过程,叫作运动的分解.
3.运动的合成与分解遵从 法则.
合运动
由合运动求分运动
矢量运算
4.合运动与分运动的四个特性
等时性 各分运动与合运动同时发生和结束,时间相同
等效性 各分运动的共同效果与合运动的效果相同
同体性 各分运动与合运动是同一物体的运动
独立性 各分运动之间互不相干,彼此独立,互不影响
5.运动的合成与分解
(1)运动的合成与分解是指位移、速度、加速度的合成与分解.其合成、分解遵循平行四边形定则.
(2)对速度v进行分解时,不能随意分解,应按物体的实际运动效果进行分解.
6.曲、直判断:
加速度(或合力)与速度方向
7.是否为匀变速运动的判断:
加速度(或合力)
互成角度的一个匀速直线运动和一个匀变速直线运动的合运动的轨迹向哪个方向弯曲?
轨迹在合初速度v0与合加速度a之间,且向合加速度一侧弯曲.
在水平桌面上放置一张纸,画有如图所示的平面直角坐标系,一个涂有颜料的小球沿y轴正方向运动(不计球与纸间的摩擦),经过原点O时,白纸从静止开始沿x轴正方向做匀加速直线运动,经过一段时间,纸面上留下的痕迹可能为( )
A
三、小船渡河问题
一条宽为d的大河,小明驾着小船从码头A出发,欲将一批货物运送到对岸的码头B.已知河水流速为v水,小船在静水中的航速为v船.
1.渡河过程中,小船参与了哪两个分运动?
2.小船如何渡河时间最短?最短时间为多少?此时渡河位移为多大?
3.小船如何渡河才能使渡河位移最小?最小位移为多大?
情况一:v水
四、关联速度模型
1.两物体通过不可伸长的轻绳(杆)相连,当两物体都发生运动,且物体运动的方向不在绳(杆)的直线上,两物体的速度是关联的..
2.处理关联速度问题的方法:首先认清哪个是合速度、哪个是分速度.物体的实际速度一定是合速度,分解时两个分速度方向应取沿绳方向和垂直绳方向.
如图所示,岸上的小车A以速度v匀速向左运动,绳跨过光滑轻质定滑轮和小船B相连.
(1)在相等的时间内,小车A和小船B运动的位移相等吗?
(2)小车A和小船B某一时刻的速度大小相等吗?如果不相等,哪个速度大?
(3)从运动的合成和分解的角度看,小船上P点的速度可以分解为哪两个分速度?
(4)若某时刻连接船的绳与水平方向的夹角为α,则船的速度是多大?
五、实验:探究平抛运动的特点
1.抛体运动:以一定的速度将物体抛出,在空气阻力 的情况下,物体只受 作用的运动.
2.平抛运动:初速度沿 方向的抛体运动.
3.平抛运动的特点:
(1)初速度沿 方向;
(2)只受 作用.
可以忽略
重力
水平
水平
重力
方案一:频闪照相(或录制视频)的方法
以抛出点为原点,建立直角坐标系
方案二:探究平抛运动竖直分运动的特点
分别改变小球距地面的高度和小锤击打的力度,即改变A球的初速度,发现两球 ,说明平抛运动在竖直方向的分运动为 .
仍同时落地
自由落体运动.
实验:探究平抛运动水平分运动的特点
平抛运动在相等时间内水平方向位移相等,平抛运动水平方向为匀速直线运动.
六、平抛运动的规律
平抛运动的速度
水平方向:不受力,加速度是0,水平方向为匀速直线运动,vx=v0.
竖直方向:只受重力,所以a=g;竖直方向的初速度为0,所以竖直方向为自由落体运动,vy=gt.
平抛运动的速度方向沿轨迹的切线方向,速度大小、方向都不断变化.
平抛运动的位移与轨迹
1.水平位移:x=v0t
2.竖直位移:y= gt2
3.轨迹方程:y= x2,由此可知平抛运动的轨迹是一条抛物线.
平抛运动的规律
七、与斜面、曲面相结合的平抛运动
从空中水平抛出垂直落到斜面上
分解速度,构建速度三角形
vx=v0
vy=gt
从斜面水平抛出又落到斜面上
分解位移,构建位移三角形
x=v0t
y= gt2
斜面外开始,要求以最短位移打到斜面
分解位移,构建位移三角形
x=v0t
y= gt2
斜面外开始,沿斜面方向落入斜面
(与斜面距离最大)
分解速度,构建速度三角形
vx=v0
vy=gt
八、平抛运动的两个重要推论
1.做平抛运动的物体在某时刻速度方向与水平方向的夹角θ、位移方向与水平方向的夹角α的关系为tan θ=2tan α.
2.做平抛运动的物体在任意时刻的速度的反向延长线一定通过此时水平位移的中点.
如图所示,AB为半圆环ACB的水平直径,C为环上的最低点,环半径为R.一个小球从A点沿AB以速度v0抛出,不计空气阻力,则下列判断正确的是( )
A.v0越大,小球从抛出到落在半圆环上经历的时间越长
B.即使v0取值不同,小球落到环上时的速度方向和水平方向的夹角也相同
C.若v0取值适当,可以使小球垂直撞击半圆环
D.无论v0取何值,小球都不可能垂直撞击半圆环
D
再见
