5.3.1 简单的轴对称图形(1)(课件)(共33张PPT)
文档属性
| 名称 | 5.3.1 简单的轴对称图形(1)(课件)(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-26 21:15:51 | ||
图片预览









文档简介
(共33张PPT)
5.3.1简单的轴对称图形(1)
第五章
生活中的轴对称
七年级数学下册(北师大版)
学习目标
1 经历探索简单图形轴对称的过程,进一步体验轴对称的特征,发展空间观念。
2 探索并掌握等腰三角形的轴对称性及其相关性质。
3 通过学生的操作与思考,使学生掌握等腰三角形和等边三角形的轴对称性及其有关性质,从而发展空间观念。
导入新课
2.在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴 ,对应线段 ,对应角 .
垂直平分
相等
相等
1.如果一个平面图形沿一条直线折叠后,直线两旁的部分能够 ,那么这个图形叫做轴对称图形,这条直线叫做 .
互相重合
对称轴
一个轴对称图形的对称轴可能是一条,也有可能
是多条.
导入新课
问题:下列图片中有你熟悉的几何图形吗?
讲授新课
等腰三角形的性质
A
B
C
等腰三角形定义:
有两条边相等的三角形, 叫做等腰三角形.
相等的两条边叫做腰,
另一条边叫做底边,
底边与腰的夹角叫做底角.
两腰所夹的角叫做顶角,
腰
腰
底边
顶角
底角
讲授新课
等腰三角形是轴对称图形吗?如果是,请找出它的对称轴.
你是如何得到问题的答案的?
直接想象
折叠操作
折叠验证
想象过程
讲授新课
找出等腰△ABC的对称轴.
等腰三角形底边的中线所在的直线.
等腰三角形底边的高所在的直线.
你同意他们的观点吗?
讲授新课
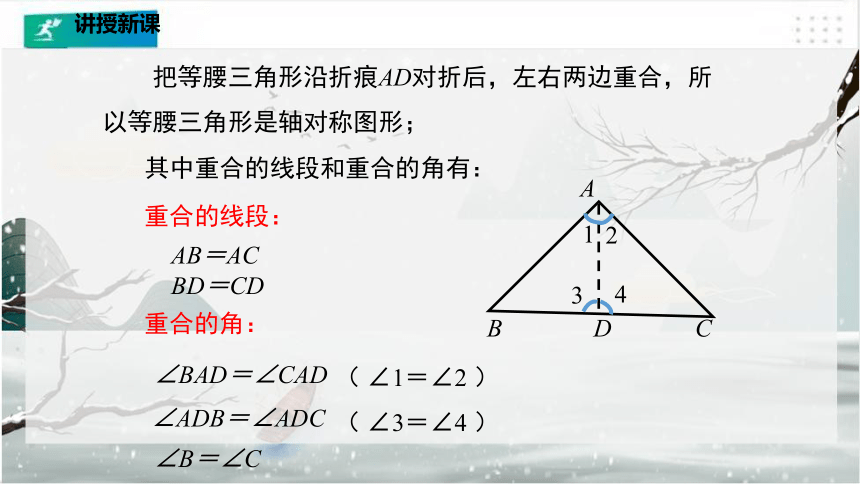
把等腰三角形沿折痕AD对折后,左右两边重合,所以等腰三角形是轴对称图形;
重合的线段:
AB=AC
BD=CD
∠BAD=∠CAD
重合的角:
B
A
C
D
其中重合的线段和重合的角有:
1
2
4
3
∠ADB=∠ADC
∠B=∠C
( ∠1=∠2 )
( ∠3=∠4 )
讲授新课
B
A
C
D
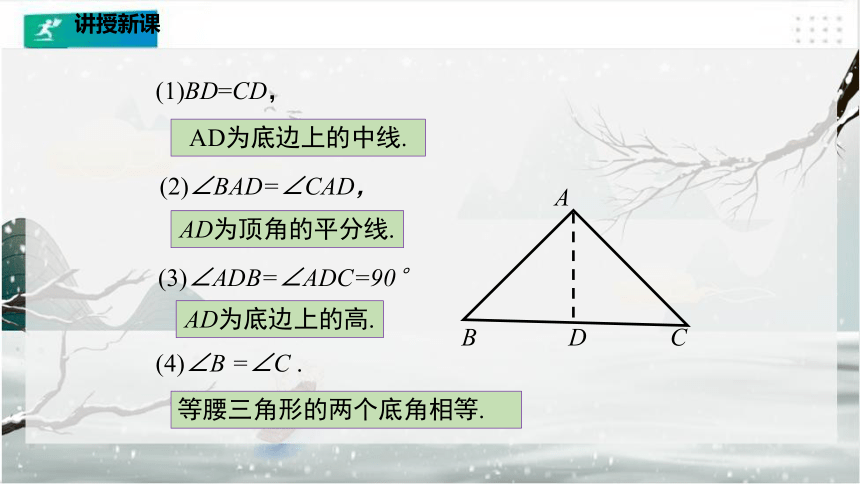
(1)BD=CD,
AD为底边上的中线.
(2)∠BAD=∠CAD,
AD为顶角的平分线.
(3)∠ADB=∠ADC=90°
AD为底边上的高.
(4)∠B =∠C .
等腰三角形的两个底角相等.
讲授新课
1.等腰三角形顶角平分线所在的直线是它的对称轴.
A
B
C
D
如图,在等腰△ABC中,AB=AC,AD是∠BAC的平分线,求证:直线AD是等腰△ABC的对称轴.
证明:
∵AD是∠BAC的平分线,
∴∠BAD=∠ CAD.
在△ABD和△ACD中,
AB=AC
∠BAD=∠ CAD
AD=AD,
∴△ABD≌△ACD(SAS).
∴直线AD是等腰△ABC的对称轴.
讲授新课
A
B
C
D
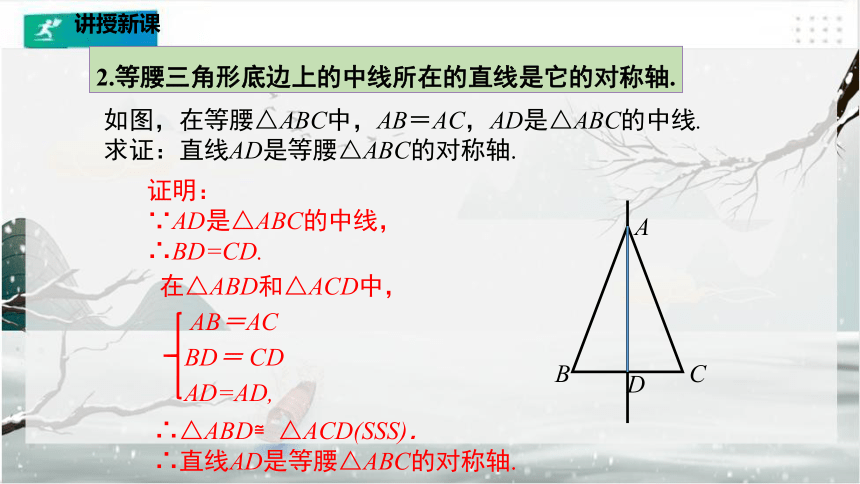
证明:
∵AD是△ABC的中线,
∴BD=CD.
在△ABD和△ACD中,
AB=AC
BD= CD
AD=AD,
∴△ABD≌△ACD(SSS).
∴直线AD是等腰△ABC的对称轴.
2.等腰三角形底边上的中线所在的直线是它的对称轴.
如图,在等腰△ABC中,AB=AC,AD是△ABC的中线.求证:直线AD是等腰△ABC的对称轴.
讲授新课
3.等腰三角形底边上的高所在的直线是它的对称轴.
A
B
C
D
如图,在等腰△ABC中,AB=AC,AD⊥BC.
求证:直线AD是等腰△ABC的对称轴.
证明:
∵AD⊥BC,
∴∠BDA=∠CDA=90°.
∴直线AD是等腰△ABC的对称轴.
在△ABD和△ACD中,
AB=AC
AD=AD,
∴△ABD≌△ACD(HL).
讲授新课
4.等腰三角形顶角平分线、底边上的中线、底边上的高重合.
A
B
C
D
证明:
在△ABD和△ACD中,
AB=AC
∠BAD=∠ CAD
AD=AD,
∴△ABD≌△ACD(SAS).
∴BD=CD,
∠BDA=∠ CDA.
如图,在等腰△ABC中,AB=AC,∠BAD=∠ CAD.
求证:AD⊥BC,BD=CD.
∵∠BDA+∠ CDA=180°,
∴∠BDA=∠ CDA=90°.
∴AD⊥BC.
讲授新课
证明:
在△ABD和△ACD中,
AB=AC
BD= CD
AD=AD,
∴△ABD≌△ACD(SSS).
∴∠BAD=∠CAD,
∠BDA=∠ CDA.
如图,在等腰△ABC中,AB=AC,BD=CD.
求证:∠BAD=∠ CAD,AD⊥BC.
4.等腰三角形顶角平分线、底边上的中线、底边上的高重合.
A
B
C
D
∵∠BDA+∠ CDA=180°,
∴∠BDA=∠ CDA=90°.
∴AD⊥BC.
讲授新课
证明:
∵AD⊥BC,
∴∠BDA=∠CDA=90°.
在Rt△ABD和Rt△ACD中,
AB=AC
AD=AD,
∴Rt△ABD≌Rt△ACD(HL).
如图,在等腰△ABC中,AB=AC,AD⊥BC.
求证:∠BAD=∠ CAD,AD⊥BC.
4.等腰三角形顶角平分线、底边上的中线、底边上的高重合.
A
B
C
D
∴∠BAD=∠CAD,
BD= CD.
讲授新课
等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
“知其一”,
“得另二”!
A
B
C
D
在△ABC中,AB=AC,
∵AD⊥BC,
∴∠BAD=∠CAD,BD=CD.
在△ABC中,AB=AC,
∵∠BAD=∠CAD,
∴AD⊥BC,BD=CD.
在△ABC中,AB=AC,
∵BD=CD,
∴∠BAD=∠CAD,AD⊥BC.
等腰三角形是轴对称图形.
等腰三角形的顶角平分线、底边上的高和底边上的中线互相重合(简称“三线合一”).
归纳总结
等腰三角形的两个底角相等.
讲授新课
等边三角形的性质
(1)等边三角形有几条对称轴?
等边三角形有三条对称轴.
等边三角形是特殊的等腰三角形.
一般到特殊!
讲授新课
(2)你能发现它的哪些特征?
等边三角形的三个内角都相等,且每个内角都是60°.
∵△ ABC是等边三角形,
∴∠A=∠B= ∠C=60°.
文字语言:
几何语言:
A
C
B
等边三角形是轴对称图形,共有三条对称轴。
等边三角形每个角的平分线和这个角的对边上的中线、高线重合(简称“三线合一”),它们所在的直线都是等边三角形的对称轴。
归纳总结
等边三角形的各角都相等,都等于60°
当堂检测
1. 一个等边三角形的对称轴共有( )
A.1条 B.2条 C.3条 D.6条
C
2.下列图形一定是轴对称图形的是( )
A.锐角三角形 B.直角三角形 C.等腰三角形
D.不等边三角形 E.钝角三角形 F.等边三角形
C、F
当堂检测
3. 如图,在△ABC中,AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为( )
A.35°
B.45°
C.55°
D.60°
C
当堂检测
4. 一个等腰三角形的周长为11 cm,其中一边长为3 cm,则其余两边长为 ( )
A.3 cm,5 cm B.4 cm,4 cm
C.3 cm,5 cm或4 cm,4 cm D.以上都不对
C
5.如果ΔABC是轴对称图形,则它的对称轴一定是( )
A. 某一条边上的高。
B. 某一条边上的中线。
C. 平分一角和这个角的对边的直线。
D. 某一个角的平分线。
C
当堂检测
6.如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB
于点E,DF⊥AC于点F,下列结论:①∠BAD=∠CAD;
②AD上任意一点到AB,AC的距离相等;③BD=CD;
④若点P在直线AD上,则PB=PC.
其中正确的是( )
A.① B.①②
C.①②③ D.①②③④
D
当堂检测
7.填空:
(1)等腰直角三角形的每一个锐角的度数是 ;
(2)如果等腰三角形的底角等于40°,那么它的顶角的度数是______ ;
(3)如果等腰三角形有一个内角等于80°,那么这个三角形的最小内角等于____________ ;
20°或50°
100°
45°
当堂检测
8.如图,AB=AE,BC=DE,∠B=∠E,AM⊥CD,垂足为M. 试说明:CM=MD.
解:如图,连接AC,AD.
在△ABC和△AED中,
所以△ABC≌△AED(SAS).
所以AC=AD.
又因为AM⊥CD,
所以CM=MD.
当堂检测
9. 用三角尺和直尺作图.(不写作法,保留作图痕迹)如图,
点A,B在直线l的同侧.(1)试在直线l上取一点M,使MA+MB的值最小;(2)试在直线l上取一点N,使NB-NA的值最大.
解:(1)如图所示:
(2)如图所示:
当堂检测
10.已知点D、E在△ABC的边BC上,AB=AC.
(1)如图①,若AD=AE,求证:BD=CE;
(2)如图②,若BD=CE,F为DE的中点,求证:AF⊥BC.
图②
图①
当堂检测
证明:(1)如图①,过A作
AG⊥BC于G.
∵AB=AC,AD=AE,
∴BG=CG,DG=EG,
∴BG-DG=CG-EG,
∴BD=CE;
(2)∵BD=CE,F为DE的中点,
∴BD+DF=CE+EF,
∴BF=CF.
∵AB=AC,∴AF⊥BC.
图②
图①
G
当堂检测
方法总结:在等腰三角形有关计算或证明中,有时需要添加辅助线,其顶角平分线、底边上的高、底边上的中线是常见的辅助线.
课堂小结
等腰三角形的性质
轴对称图形
等腰三角形
三线合一
等边对等角
等边三角形的性质
三线合一
轴对称图形
各角都相等
,都为60度
https://www.21cnjy.com/help/help_extract.php
5.3.1简单的轴对称图形(1)
第五章
生活中的轴对称
七年级数学下册(北师大版)
学习目标
1 经历探索简单图形轴对称的过程,进一步体验轴对称的特征,发展空间观念。
2 探索并掌握等腰三角形的轴对称性及其相关性质。
3 通过学生的操作与思考,使学生掌握等腰三角形和等边三角形的轴对称性及其有关性质,从而发展空间观念。
导入新课
2.在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴 ,对应线段 ,对应角 .
垂直平分
相等
相等
1.如果一个平面图形沿一条直线折叠后,直线两旁的部分能够 ,那么这个图形叫做轴对称图形,这条直线叫做 .
互相重合
对称轴
一个轴对称图形的对称轴可能是一条,也有可能
是多条.
导入新课
问题:下列图片中有你熟悉的几何图形吗?
讲授新课
等腰三角形的性质
A
B
C
等腰三角形定义:
有两条边相等的三角形, 叫做等腰三角形.
相等的两条边叫做腰,
另一条边叫做底边,
底边与腰的夹角叫做底角.
两腰所夹的角叫做顶角,
腰
腰
底边
顶角
底角
讲授新课
等腰三角形是轴对称图形吗?如果是,请找出它的对称轴.
你是如何得到问题的答案的?
直接想象
折叠操作
折叠验证
想象过程
讲授新课
找出等腰△ABC的对称轴.
等腰三角形底边的中线所在的直线.
等腰三角形底边的高所在的直线.
你同意他们的观点吗?
讲授新课
把等腰三角形沿折痕AD对折后,左右两边重合,所以等腰三角形是轴对称图形;
重合的线段:
AB=AC
BD=CD
∠BAD=∠CAD
重合的角:
B
A
C
D
其中重合的线段和重合的角有:
1
2
4
3
∠ADB=∠ADC
∠B=∠C
( ∠1=∠2 )
( ∠3=∠4 )
讲授新课
B
A
C
D
(1)BD=CD,
AD为底边上的中线.
(2)∠BAD=∠CAD,
AD为顶角的平分线.
(3)∠ADB=∠ADC=90°
AD为底边上的高.
(4)∠B =∠C .
等腰三角形的两个底角相等.
讲授新课
1.等腰三角形顶角平分线所在的直线是它的对称轴.
A
B
C
D
如图,在等腰△ABC中,AB=AC,AD是∠BAC的平分线,求证:直线AD是等腰△ABC的对称轴.
证明:
∵AD是∠BAC的平分线,
∴∠BAD=∠ CAD.
在△ABD和△ACD中,
AB=AC
∠BAD=∠ CAD
AD=AD,
∴△ABD≌△ACD(SAS).
∴直线AD是等腰△ABC的对称轴.
讲授新课
A
B
C
D
证明:
∵AD是△ABC的中线,
∴BD=CD.
在△ABD和△ACD中,
AB=AC
BD= CD
AD=AD,
∴△ABD≌△ACD(SSS).
∴直线AD是等腰△ABC的对称轴.
2.等腰三角形底边上的中线所在的直线是它的对称轴.
如图,在等腰△ABC中,AB=AC,AD是△ABC的中线.求证:直线AD是等腰△ABC的对称轴.
讲授新课
3.等腰三角形底边上的高所在的直线是它的对称轴.
A
B
C
D
如图,在等腰△ABC中,AB=AC,AD⊥BC.
求证:直线AD是等腰△ABC的对称轴.
证明:
∵AD⊥BC,
∴∠BDA=∠CDA=90°.
∴直线AD是等腰△ABC的对称轴.
在△ABD和△ACD中,
AB=AC
AD=AD,
∴△ABD≌△ACD(HL).
讲授新课
4.等腰三角形顶角平分线、底边上的中线、底边上的高重合.
A
B
C
D
证明:
在△ABD和△ACD中,
AB=AC
∠BAD=∠ CAD
AD=AD,
∴△ABD≌△ACD(SAS).
∴BD=CD,
∠BDA=∠ CDA.
如图,在等腰△ABC中,AB=AC,∠BAD=∠ CAD.
求证:AD⊥BC,BD=CD.
∵∠BDA+∠ CDA=180°,
∴∠BDA=∠ CDA=90°.
∴AD⊥BC.
讲授新课
证明:
在△ABD和△ACD中,
AB=AC
BD= CD
AD=AD,
∴△ABD≌△ACD(SSS).
∴∠BAD=∠CAD,
∠BDA=∠ CDA.
如图,在等腰△ABC中,AB=AC,BD=CD.
求证:∠BAD=∠ CAD,AD⊥BC.
4.等腰三角形顶角平分线、底边上的中线、底边上的高重合.
A
B
C
D
∵∠BDA+∠ CDA=180°,
∴∠BDA=∠ CDA=90°.
∴AD⊥BC.
讲授新课
证明:
∵AD⊥BC,
∴∠BDA=∠CDA=90°.
在Rt△ABD和Rt△ACD中,
AB=AC
AD=AD,
∴Rt△ABD≌Rt△ACD(HL).
如图,在等腰△ABC中,AB=AC,AD⊥BC.
求证:∠BAD=∠ CAD,AD⊥BC.
4.等腰三角形顶角平分线、底边上的中线、底边上的高重合.
A
B
C
D
∴∠BAD=∠CAD,
BD= CD.
讲授新课
等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
“知其一”,
“得另二”!
A
B
C
D
在△ABC中,AB=AC,
∵AD⊥BC,
∴∠BAD=∠CAD,BD=CD.
在△ABC中,AB=AC,
∵∠BAD=∠CAD,
∴AD⊥BC,BD=CD.
在△ABC中,AB=AC,
∵BD=CD,
∴∠BAD=∠CAD,AD⊥BC.
等腰三角形是轴对称图形.
等腰三角形的顶角平分线、底边上的高和底边上的中线互相重合(简称“三线合一”).
归纳总结
等腰三角形的两个底角相等.
讲授新课
等边三角形的性质
(1)等边三角形有几条对称轴?
等边三角形有三条对称轴.
等边三角形是特殊的等腰三角形.
一般到特殊!
讲授新课
(2)你能发现它的哪些特征?
等边三角形的三个内角都相等,且每个内角都是60°.
∵△ ABC是等边三角形,
∴∠A=∠B= ∠C=60°.
文字语言:
几何语言:
A
C
B
等边三角形是轴对称图形,共有三条对称轴。
等边三角形每个角的平分线和这个角的对边上的中线、高线重合(简称“三线合一”),它们所在的直线都是等边三角形的对称轴。
归纳总结
等边三角形的各角都相等,都等于60°
当堂检测
1. 一个等边三角形的对称轴共有( )
A.1条 B.2条 C.3条 D.6条
C
2.下列图形一定是轴对称图形的是( )
A.锐角三角形 B.直角三角形 C.等腰三角形
D.不等边三角形 E.钝角三角形 F.等边三角形
C、F
当堂检测
3. 如图,在△ABC中,AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为( )
A.35°
B.45°
C.55°
D.60°
C
当堂检测
4. 一个等腰三角形的周长为11 cm,其中一边长为3 cm,则其余两边长为 ( )
A.3 cm,5 cm B.4 cm,4 cm
C.3 cm,5 cm或4 cm,4 cm D.以上都不对
C
5.如果ΔABC是轴对称图形,则它的对称轴一定是( )
A. 某一条边上的高。
B. 某一条边上的中线。
C. 平分一角和这个角的对边的直线。
D. 某一个角的平分线。
C
当堂检测
6.如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB
于点E,DF⊥AC于点F,下列结论:①∠BAD=∠CAD;
②AD上任意一点到AB,AC的距离相等;③BD=CD;
④若点P在直线AD上,则PB=PC.
其中正确的是( )
A.① B.①②
C.①②③ D.①②③④
D
当堂检测
7.填空:
(1)等腰直角三角形的每一个锐角的度数是 ;
(2)如果等腰三角形的底角等于40°,那么它的顶角的度数是______ ;
(3)如果等腰三角形有一个内角等于80°,那么这个三角形的最小内角等于____________ ;
20°或50°
100°
45°
当堂检测
8.如图,AB=AE,BC=DE,∠B=∠E,AM⊥CD,垂足为M. 试说明:CM=MD.
解:如图,连接AC,AD.
在△ABC和△AED中,
所以△ABC≌△AED(SAS).
所以AC=AD.
又因为AM⊥CD,
所以CM=MD.
当堂检测
9. 用三角尺和直尺作图.(不写作法,保留作图痕迹)如图,
点A,B在直线l的同侧.(1)试在直线l上取一点M,使MA+MB的值最小;(2)试在直线l上取一点N,使NB-NA的值最大.
解:(1)如图所示:
(2)如图所示:
当堂检测
10.已知点D、E在△ABC的边BC上,AB=AC.
(1)如图①,若AD=AE,求证:BD=CE;
(2)如图②,若BD=CE,F为DE的中点,求证:AF⊥BC.
图②
图①
当堂检测
证明:(1)如图①,过A作
AG⊥BC于G.
∵AB=AC,AD=AE,
∴BG=CG,DG=EG,
∴BG-DG=CG-EG,
∴BD=CE;
(2)∵BD=CE,F为DE的中点,
∴BD+DF=CE+EF,
∴BF=CF.
∵AB=AC,∴AF⊥BC.
图②
图①
G
当堂检测
方法总结:在等腰三角形有关计算或证明中,有时需要添加辅助线,其顶角平分线、底边上的高、底边上的中线是常见的辅助线.
课堂小结
等腰三角形的性质
轴对称图形
等腰三角形
三线合一
等边对等角
等边三角形的性质
三线合一
轴对称图形
各角都相等
,都为60度
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
