2021—2022学年沪科版数学七年级下册7.4 综合与实践--排队问题课件(共19张PPT)
文档属性
| 名称 | 2021—2022学年沪科版数学七年级下册7.4 综合与实践--排队问题课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 321.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
7.4综合与实践
--排队问题
问题1.某服务窗口办理业务,按先到达先服务的方式服务。该窗口每2分钟服务一位顾客,已知当窗口开始工作时,已经有6位顾客在等待,在窗口开始工作1分钟后,又有一位新顾客到达,且预计以后每5分钟都有一位新顾客到达:
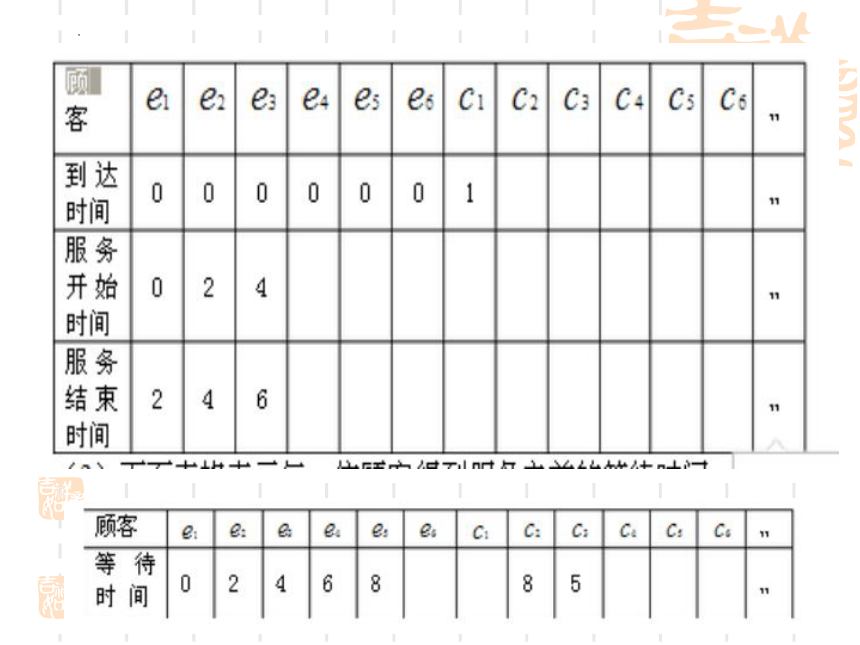
(1)设 , , , , , ,表示窗口开始工作时已经在等待的6位顾客, , , , 表示窗口开始工作后按先后顺序到达的新顾客,完成下表:
(2)下面表格表示每一位顾客得到服务之前的等待时间,完成下面的表格:
(5)求平均等待时间是多少?
(3)根据表格,哪一位是第一位到达服务机构而不需排队的?求出他的到达时间
(4)在第一位不需排队的顾客到达之前,该窗口已经服务了多少位顾客?为这些顾客服务共花费多长时间?
问题2 问题1 中,当窗口开始工作时,已经有10位顾客在等待,且当新顾客 离开时,排队现象消失,即 为第一位不需要排队的新顾客: (1)在第一位不需要排队的“新顾客” 到达之前,已经服务了多少位顾客?共花费了多长时间?
10+n位
2(10+n)
(2)“新顾客” 到达时间是什么?
5n+1
(3)“新顾客” 到达后不排队的条件是什么?
在“新顾客” 到达之前,该窗口为顾客服务时间小于等于“新顾客” 的到达时间。
(4)问题解决吗?能否确定n+1的值?还需要什么条件?
新顾客”Cn到达之前,该窗口为顾客服务的时间大于“新顾客” Cn的到达时间。
在一次数学测验中,老师按照“先写完,先批改”的原则给学生进行面批试卷,老师每2min批改一份试卷,已知老师开始进行批改时,已有3位同学答题完毕到达讲台边等待,在老师开始面批1min后,又有一位“新同学”答题完毕,且预计后面每5min都有一位“新同学”答题完毕。
感知生活
每2min批改一份试卷
3位同学
等待
1min
每5min
同 学 …
到达时间 0 0 0 1 ...
开始时间 0 2 …
设 , , 表示当老师开始批改时已经到达讲台在等待的3位同学; , ,… ,表示在老师开始批改以后,按先后顺序到达的“新同学”,请将下面表格补充完整
(这里假设 , , 的到达时间为0)
等待时间 …
11
16
21
6
6
8
11
4
16
21
0
5
2
0
0
0
2
4
排队消失前,每位同学的面批开始时间和已花费时间之有什么关系呢?
总结知识
2、你能用含有 的代数式表示 的到达时间吗?
3、当到达时间和开始时间满足什么关系时排队就会消失呢?
1、用关于 的代数式表示,在第一位不需要排队的“新同学” 到达之前,老师已为多少同学面批作业?批改这些作业共花费了多长时间?
1、当老师开始改卷时如果已经已经有6位同学在等待(其他条件不变),哪一位是第一个不需排队的同学呢?
2、他的到达时间是多少?
3、此时为前面同学面批一共花费了多少时间?
4、如果已经有10位同学在等待了,结果又如何呢?
运用知识
同学们感受到
不等式的妙用了吗?
解决问题
1、老师面批试卷时如果每6分钟面批一位同学,排队现象还会消失吗?
2、在这样的情况下,我们可以通过什么途径来解决排队问题呢?
面对现实生活中的种种排队现象我们要怎么处理呢?
本节课你收获了哪些数学知识和方法,谈谈你自己的学习体会。
课堂小结
实际问题
数学问题
数学模型
实际问题
抽象
解决
构造
7.4综合与实践
--排队问题
问题1.某服务窗口办理业务,按先到达先服务的方式服务。该窗口每2分钟服务一位顾客,已知当窗口开始工作时,已经有6位顾客在等待,在窗口开始工作1分钟后,又有一位新顾客到达,且预计以后每5分钟都有一位新顾客到达:
(1)设 , , , , , ,表示窗口开始工作时已经在等待的6位顾客, , , , 表示窗口开始工作后按先后顺序到达的新顾客,完成下表:
(2)下面表格表示每一位顾客得到服务之前的等待时间,完成下面的表格:
(5)求平均等待时间是多少?
(3)根据表格,哪一位是第一位到达服务机构而不需排队的?求出他的到达时间
(4)在第一位不需排队的顾客到达之前,该窗口已经服务了多少位顾客?为这些顾客服务共花费多长时间?
问题2 问题1 中,当窗口开始工作时,已经有10位顾客在等待,且当新顾客 离开时,排队现象消失,即 为第一位不需要排队的新顾客: (1)在第一位不需要排队的“新顾客” 到达之前,已经服务了多少位顾客?共花费了多长时间?
10+n位
2(10+n)
(2)“新顾客” 到达时间是什么?
5n+1
(3)“新顾客” 到达后不排队的条件是什么?
在“新顾客” 到达之前,该窗口为顾客服务时间小于等于“新顾客” 的到达时间。
(4)问题解决吗?能否确定n+1的值?还需要什么条件?
新顾客”Cn到达之前,该窗口为顾客服务的时间大于“新顾客” Cn的到达时间。
在一次数学测验中,老师按照“先写完,先批改”的原则给学生进行面批试卷,老师每2min批改一份试卷,已知老师开始进行批改时,已有3位同学答题完毕到达讲台边等待,在老师开始面批1min后,又有一位“新同学”答题完毕,且预计后面每5min都有一位“新同学”答题完毕。
感知生活
每2min批改一份试卷
3位同学
等待
1min
每5min
同 学 …
到达时间 0 0 0 1 ...
开始时间 0 2 …
设 , , 表示当老师开始批改时已经到达讲台在等待的3位同学; , ,… ,表示在老师开始批改以后,按先后顺序到达的“新同学”,请将下面表格补充完整
(这里假设 , , 的到达时间为0)
等待时间 …
11
16
21
6
6
8
11
4
16
21
0
5
2
0
0
0
2
4
排队消失前,每位同学的面批开始时间和已花费时间之有什么关系呢?
总结知识
2、你能用含有 的代数式表示 的到达时间吗?
3、当到达时间和开始时间满足什么关系时排队就会消失呢?
1、用关于 的代数式表示,在第一位不需要排队的“新同学” 到达之前,老师已为多少同学面批作业?批改这些作业共花费了多长时间?
1、当老师开始改卷时如果已经已经有6位同学在等待(其他条件不变),哪一位是第一个不需排队的同学呢?
2、他的到达时间是多少?
3、此时为前面同学面批一共花费了多少时间?
4、如果已经有10位同学在等待了,结果又如何呢?
运用知识
同学们感受到
不等式的妙用了吗?
解决问题
1、老师面批试卷时如果每6分钟面批一位同学,排队现象还会消失吗?
2、在这样的情况下,我们可以通过什么途径来解决排队问题呢?
面对现实生活中的种种排队现象我们要怎么处理呢?
本节课你收获了哪些数学知识和方法,谈谈你自己的学习体会。
课堂小结
实际问题
数学问题
数学模型
实际问题
抽象
解决
构造
